JavaScript图形实例：正多边形
圆心位于坐标原点，半径为R的圆的参数方程为
X=R*COS(θ)
Y=R*SIN(θ)
在圆上取N个等分点，将这N个点首尾连接N条边，可以得到一个正N边形。
1．正多边形阵列
构造一个8行8列的正N（N为3~10）边形阵列。编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>正多边形阵列</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,400,400);
context.fillStyle="yellow";
context.strokeStyle="red";
context.lineWidth=1;
context.beginPath();
for (px=30;px<390;px+=45)
for (py=30;py<390;py+=45)
{
n=((px-30)/45+(py-30)/45)%8+3;
for (i=0;i<=n;i++)
{
x1=20*Math.cos(i*Math.PI*2/n);
y1=20*Math.sin(i*Math.PI*2/n);
x=px+x1;
y=py+y1;
if (i==0)
context.moveTo(x,y);
else
context.lineTo(x,y);
}
}
context.closePath();
context.stroke();
context.fill();
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="400" height="400">您的浏览器不支持canvas！
</canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出正3~10边形阵列，如图1所示。
图1 正3~10边形阵列
2．边长相等的正多边形
图1中的正N边形通过在圆周上取N等分点得到的，它们的外接圆的半径均相等，但各自的边长并不相等。若要绘制出边长相等的正N边形，可以编写如下的HTML文件。
<!DOCTYPE html>
<head>
<title>边长相等的正多边形</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,400,300);
context.strokeStyle="blue";
context.lineWidth=2;
var x0=150;
var y0=30;
context.beginPath();
for (n=3;n<=10;n++)
{
dig=6.28318/n;
context.moveTo(x0,y0);
x=x0;
y=y0;
for(i=0;i<n;i++)
{
x=x+80*Math.cos(i*dig);
y=y+80*Math.sin(i*dig);
context.lineTo(x,y);
}
context.lineTo(x0,y0);
}
context.stroke();
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="400" height="300">您的浏览器不支持canvas！
</canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出边长相等的正多边形（从正三角形到正十边形），如图2所示。
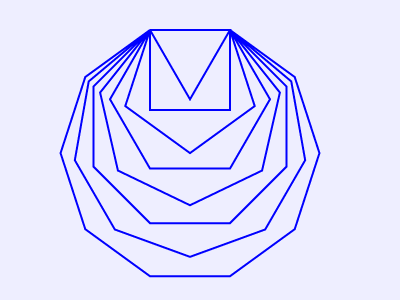
图2 边长相等的正多边形
3．漂亮的圆盘
在圆周上取N等分点，将这N个等分点两两用线段相连，共连N*(N-1)/2条边，可以绘制出圆盘图案。编写的HTML代码如下。
<!DOCTYPE html>
<head>
<title>圆盘图案</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,400,400);
context.strokeStyle="red";
context.lineWidth=1;
var x=new Array(25);
var y=new Array(25);
var r = 180;
var n=25;
for (i = 0; i <n; i++)
{
x[i] = r * Math.cos(2 *Math.PI * i/n) + 200;
y[i] = r * Math.sin(2 *Math.PI * i/n) + 200;
}
context.beginPath();
for (i = 0; i <n-1; i++)
{
for (j = i + 1; j <n ; j++)
{
context.moveTo(x[i],y[i]);
context.lineTo(x[j],y[j]);
}
}
context.closePath();
context.stroke();
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="400" height="400">您的浏览器不支持canvas！
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出漂亮的圆盘图案，如图3所示。
图3 圆盘图案
4．顶点在圆周上的连续线段
前面例子中，圆周上取点的参数方程的夹角θ都在0~2π之间，若将θ乘以一个参数k，可绘制出一些有趣的图形。编写的HTML文件内容如下。
<!DOCTYPE html>
<head>
<title>顶点在圆周上的连续线段</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,300,300);
context.fillStyle = "cyan";
context.strokeStyle = 'red';
context.lineWidth=1;
var k=11;
var dig=Math.PI/12*k;
var radius=100;
var dx = 150;
var dy = 150;
context.beginPath();
var x = radius*Math.sin(0)+dx;
var y = radius*Math.cos(0)+dy;
context.moveTo(x,y);
for(var i = 1; i < 24; i++)
{
var x = radius*Math.sin(i * dig);
var y = radius*Math.cos(i * dig);
context.lineTo(dx+x,dy+y);
}
context.closePath();
context.fill();
context.stroke();
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="300" height="300">您的浏览器不支持canvas！
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图4所示的图案。
图4 顶点在圆周上的连续线段
仿图4图形绘制的方法，我们不绘制直线，而是绘制贝塞尔曲线。编写如下的HTML文件。
<!DOCTYPE html>
<head>
<title>终点分布在圆周上的贝塞尔曲线</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEDD";
context.fillRect(0,0,300,300);
context.fillStyle = 'cyan';
context.strokeStyle = 'red';
context.globalCompositeOperation ='and';
context.lineWidth=1;
var dig=Math.PI/15*11;
var radius=100;
var dx = 150;
var dy = 150;
context.beginPath();
for(var i = 0; i < 30; i++)
{
var x = radius*Math.sin(i * dig);
var y = radius*Math.cos(i * dig);
context.bezierCurveTo(dx+x,dy+y-100,dx+x+100,dy+y,dx+x,dy+y);
}
context.closePath();
context.fill();
context.stroke();
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="300" height="300">您的浏览器不支持canvas！
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图5所示的图案。
图5 终点分布在圆周上的贝塞尔曲线
