矩阵乘法（五）：置换

      矩阵乘法在一些置换问题上有着很好的应用，特别置换次数较多时，采用矩阵快速幂运算可以加快运算过程。

      任意一个置换都能够表示成矩阵的形式。比如，将序列1  2  3  4 置换为 3  1  2  4，相当于以下的矩阵乘法：

          

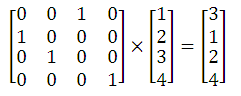
      一般来说，对于序列1, 2, ..., n，若给出置换方法a₁,a₂,...,a_n ，该置换方法表示将原序列的第pi位置上的元素换到第i位置上。

        则可以构造置换矩阵P为： P[ai][i]=1 (1<=i<=n)， 其余元素全为0。

        显然，置换矩阵每行只有一个元素为1，其余为0。

        另外，构造的置换矩阵都是可逆的，并且它的逆矩阵等于它的转置矩阵。

【例1】解码字符串。

      给定n个数，代表一个置换。一个长度为n的字符串s经过m次置换后变成另一个字符串t。

      例如，输入5个数：2  3  1  5  4 代表一个置换操作。字符串s为“hello”，经过3次置换操作

"hello"  ->  "elhol"  ->  "lhelo"  ->  "helol"后，可得到字符串t为“helol”。

      输入n、m和结果字符串t，输出转换前的原字符串s。

      （1）编程思路。

       由置换规则  2 3 1 5 4，可以快速构造用于字符串s转换到t的置换矩阵P。

   

 

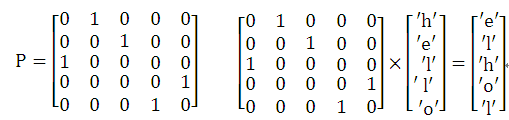
       而从字符串t转换到s显然是逆操作，而置换矩阵的逆矩阵就是其转置矩阵。因此，用于本题的置换矩阵P^T应为：    

     

 

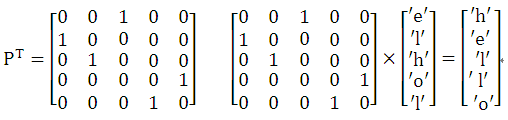
      构造好置换矩阵后，m次操作就是置换矩阵的m次幂，之后再乘以初始序列{1 2 3 4 ....n}，然后输出相应位置的字符就可以了。

      （2）源程序。

#include <stdio.h>
#include <string.h>
struct Matrix
{
      int mat[81][81]; // 存储矩阵中各元素
};
Matrix matMul(Matrix a ,Matrix b,int n)
{
      Matrix c;
      memset(c.mat,0,sizeof(c.mat));
      int i,j,k;
      for (k = 1; k<=n ; k++)
           for (i=1 ;i<=n ; i++)
               if (a.mat[i][k]!=0)
                   for (j = 1 ;j<=n ;j++)
                        c.mat[i][j] = (c.mat[i][j] + a.mat[i][k] * b.mat[k][j]) ;
      return c;
}
Matrix quickMatPow(Matrix a ,int n,int b) // n阶矩阵a快速b次幂
{
      Matrix c;
      memset(c.mat ,0 ,sizeof(c.mat));
      int i;
      for (i = 1 ;i <= n ;i++)
            c.mat[i][i] = 1;
      while (b!=0)
      {
           if (b & 1)
                c = matMul(c ,a ,n); // c=c*a;
           a = matMul(a ,a ,n); // a=a*a
           b /= 2;
      }
      return c;
}
int main()
{
      int n,m,p[81],i;
      Matrix a,b,ans;
      char str[82];
      while (scanf("%d%d",&n,&m) && n!=0 && m!=0)
      {
            memset(b.mat,0,sizeof(b.mat));
            for (i=1;i<=n;i++)
                 b.mat[1][i]=i;
            memset(a.mat,0,sizeof(a.mat));
            for (i=1;i<=n;i++)
            {
                  scanf("%d",&p[i]);
                  a.mat[i][p[i]]=1;
            }
            getchar();
            gets(str);
            ans=quickMatPow(a,n,m);
            ans=matMul(b,ans,n);
            for (i=1;i<=n;i++)
                  printf("%c",str[ans.mat[1][i]-1]);
            printf("\n");
      }
      return 0;
}

      将此源程序提交给HDU 2371 “Decode the Strings”，可以Accepted。

【例2】送给圣诞夜的礼品。

      已知序列1,2,3,…,n，给出m个置换操作， 例如某个置换操作 6 1 3 7 5 2 4，表示把6位置上的元素换到1位置上，1位置上的元素换到2位置上…。    

      求原序列为1,2,3,……,n的序列按给出的m个置换操作的顺序进行k次置换后得到的新序列。若k>m，则第m+1次置换操作做第1个置换操作，第m+2次置换操作做第2个置换操作，…。

     数据说明： 1<=n<=100；1<=m<=10；1<=k<=2^31-1。

      本题完整的描述可以参看 https://vijos.org/p/1049。

      （1）编程思路。

     搞懂了例1，本题就容易入手了。m 个置换操作需要构造m个置换矩阵。

     构造好置换矩阵后，先将m个置换矩阵乘起来，得到ans矩阵，则此时的ans矩阵相当进行了m次操作；再将ans矩阵进行k/m次幂，此时相当进行了k次操作。当然，由于k不一定整除m，因此还需按m个置换操作的顺序进行k%m次的置换操作。

      （2）源程序。

#include <stdio.h>
#include <string.h>
struct Matrix
{
      int mat[101][101]; // 存储矩阵中各元素
};
Matrix p[11];
Matrix matMul(Matrix a ,Matrix b,int n)
{
      Matrix c;
      memset(c.mat,0,sizeof(c.mat));
      int i,j,k;
      for (k = 1; k<=n ; k++)
          for (i=1 ;i<=n ; i++)
               if (a.mat[i][k]!=0)
                  for (j = 1 ;j<=n ;j++)
                      c.mat[i][j] = (c.mat[i][j] + a.mat[i][k] * b.mat[k][j]) ;
      return c;
}
Matrix quickMatPow(Matrix a ,int n,int b) // n阶矩阵a快速b次幂
{
      Matrix c;
      memset(c.mat ,0 ,sizeof(c.mat));
      int i;
      for (i = 1 ;i <= n ;i++)
          c.mat[i][i] = 1;
       while (b!=0)
      {
           if (b & 1)
               c = matMul(c ,a ,n); // c=c*a;
           a = matMul(a ,a ,n); // a=a*a
           b /= 2;
      }
      return c;
}
int main()
{
      int n,m,k,i,j,num,a[101];
      Matrix ans;
      scanf("%d%d%d",&n,&m,&k);
      for (i=0;i<m;i++)
      {
           memset(p[i].mat,0,sizeof(p[i].mat));
           for (j=1;j<=n;j++)
           {
                 scanf("%d",&num);
                 p[i].mat[j][num]=1;         // 构造的置换矩阵
           }
      }
      memset(ans.mat,0,sizeof(ans.mat));
      for (i=1;i<=n;i++)
            ans.mat[i][i]=1;
      for (i=0;i<m;i++)
            ans=matMul(p[i],ans,n);      // m个置换矩阵先乘起来，注意是左乘
      ans=quickMatPow(ans,n,k/m);
      for (i=0;i<k%m;i++)
            ans=matMul(p[i],ans,n);    // 剩余的k%m个矩阵相乘，代表剩余的k%m次操作
      memset(a,0,sizeof(a));
      for (i=1;i<=n;i++)
          for (j=1;j<=n;j++)
               a[i]=a[i]+(ans.mat[i][j])*j;
      for (i=1;i<=n;i++)
            printf("%d ",a[i]);
      printf("\n");
      return 0;
}