高精度计算(二):大整数乘法
【例1】两个大整数乘法。
输入两个不超过200位的非负大整数a和b,求a×b的值。
(1)编程思路。
用 unsigned num1[200]和num2[200]分别存放两个乘数,用result[400]来存放积。计算的中间结果也都存在result 中。result 长度取400 是因为两个200 位的数相乘,积最多会有400 位。num1[0], num2[0], result[0]都表示个位。
计算的过程基本上和小学生列竖式做乘法相同。为编程方便,并不急于处理进位,而将
进位问题留待最后统一处理。
图1给出了753×68的计算过程。描述如下:

1)先依次计算753的各位数字与8的乘积,并加到result数组的相应单元中。result数组的全部元素的初始值均为0。
2)再依次计算753的各位数字与6的乘积,并加到result数组的相应单元中。
3)乘法过程完毕。从 result[0]开始向高位逐位处理进位问题。result[0]留下4,
把2 加到result[1]上,result[1]变为60 后,应留下0,把6 加到result[2]上……最终使
得result 里的每个元素都是1 位数,结果就算出来了。
在乘法过程中,num1的第i 位和num2的第j 位相乘所得的数,一定是要累加到
result的第i+j 位上。这里i, j 都是从右往左,从0 开始数。
(2)源程序。(将此源程序提交给POJ 2389 “Bull Math”,可以Accepted)
#include <stdio.h>
#include <string.h>
#define MAX_LEN 201
void bigNumMul(char a[],char b[],char c[])
{
int i,j,n1,n2;
int num1[MAX_LEN]={0},num2[MAX_LEN]={0},result[2*MAX_LEN]={0};
// 将a和b中存储的字符串形式的整数转换到num1和num2中去,
// num1[0]对应于个位、num1[1]对应于十位、……
n1 = strlen(a);
j = 0;
for (i = n1 - 1;i >= 0 ; i --)
num1[j++] = a[i] - '0';
n2 = strlen(b);
j = 0;
for (i = n2 - 1;i >= 0 ; i --)
num2[j++] = b[i] - '0';
for (i=0;i < n2; i++ )
{
for (j=0; j<n1; j++)
result[i+j] += num2[i]*num1[j]; // 两数第i, j 位相乘,累加到结果的第i+j 位
}
// 统一处理进位问题
for( i = 0; i < MAX_LEN * 2; i ++ ) {
if (result[i] >= 10)
{
result[i+1] += result[i] / 10;
result[i] %= 10;
}
}
bool isBeginZero = false;
j=0;
for (i=n1+n2-1; i>=0; i--)
if (isBeginZero)
c[j++]=result[i]+'0';
else if (result[i]!=0)
{
c[j++]=result[i]+'0';
isBeginZero = true;
}
if (!isBeginZero) c[j++]='0';
c[j]='\0';
}
int main()
{
char a[MAX_LEN],b[MAX_LEN],c[2*MAX_LEN];
scanf("%s",a);
scanf("%s",b);
bigNumMul(a,b,c);
printf("%s\n",c);
return 0;
}
(3)问题扩展。
下面我们来讨论如何完成一个大整数a和一个int型整型变量b的相乘。
图2给出了753×68的另一种计算过程。描述如下:
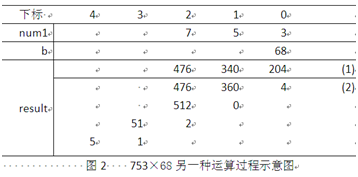
1)先依次计算753的各位数字与68的乘积,并存入到result数组的相应单元中。
2)乘法过程完毕。从 result[0]开始向高位逐位处理进位问题。result[0]留下4,
把20 加到result[1]上,result[1]变为360 后,应留下0,把36 加到result[2]上……最终使
得result 里的每个元素都是1 位数,结果就算出来了。
按这个思路可以实现一个大整数与int型整型变量相乘。源程序如下:
#include <stdio.h>
#include <string.h>
#define MAX_LEN 201
void bigNumMul(char a[],int b,char c[])
{
int i,j,n1,n2,t;
int num[MAX_LEN]={0},result[MAX_LEN+10]={0};
// 将a和b中存储的字符串形式的整数转换到num1和num2中去,
// num1[0]对应于个位、num1[1]对应于十位、……
n1 = strlen(a);
j = 0;
for (i = n1 - 1;i >= 0 ; i --)
num[j++] = a[i] - '0';
n2 =0;
t=b;
do {
n2++;
t=t/10;
} while (t!=0);
for (i=0;i < n1; i++)
result[i] = num[i]*b;
// 统一处理进位问题
for (i = 0; i < n1+n2; i++)
{
if (result[i] >= 10)
{
result[i+1] += result[i] / 10;
result[i] %= 10;
}
}
bool isBeginZero = false;
j=0;
for (i=n1+n2-1; i>=0; i--)
if (isBeginZero)
c[j++]=result[i]+'0';
else if (result[i]!=0)
{
c[j++]=result[i]+'0';
isBeginZero = true;
}
if (!isBeginZero) c[j++]='0';
c[j]='\0';
}
int main()
{
char a[MAX_LEN],c[MAX_LEN+10];
int b;
scanf("%s",a);
scanf("%d",&b);
bigNumMul(a,b,c);
printf("%s\n",c);
return 0;
}
【例2】Exponentiation (POJ 1001)。
Description
Problems involving the computation of exact values of very large magnitude and precision are common. For example, the computation of the national debt is a taxing experience for many computer systems.
This problem requires that you write a program to compute the exact value of Rn where R is a real number ( 0.0 < R < 99.999 ) and n is an integer such that 0 < n <= 25.
Input
The input will consist of a set of pairs of values for R and n. The R value will occupy columns 1 through 6, and the n value will be in columns 8 and 9.
Output
The output will consist of one line for each line of input giving the exact value of R^n. Leading zeros should be suppressed in the output. Insignificant trailing zeros must not be printed. Don't print the decimal point if the result is an integer.
Sample Input
95.123 12
0.4321 20
5.1234 15
6.7592 9
98.999 10
1.0100 12
Sample Output
548815620517731830194541.899025343415715973535967221869852721
.00000005148554641076956121994511276767154838481760200726351203835429763013462401
43992025569.928573701266488041146654993318703707511666295476720493953024
29448126.764121021618164430206909037173276672
90429072743629540498.107596019456651774561044010001
1.126825030131969720661201
(1)编程思路。
由于输入的R可能是一个小数,因此先求出R的小数点后有多少位小数(pos),然后将小数点去掉,使得R变成一个整数,然后采用例1中的函数void bigNumMul(char a[],char b[],char c[])用循环求得Rn 。之后,在结果中正确插入小数点即可。
(2)源程序。
#include <stdio.h>
#include <string.h>
#define MAX_LEN 201
void bigNumMul(char a[],char b[],char c[])
{
int i,j,n1,n2;
int num1[MAX_LEN]={0},num2[MAX_LEN]={0},result[2*MAX_LEN]={0};
// 将a和b中存储的字符串形式的整数转换到num1和num2中去,
// num1[0]对应于个位、num1[1]对应于十位、……
n1 = strlen(a);
j = 0;
for (i = n1 - 1;i >= 0 ; i --)
num1[j++] = a[i] - '0';
n2 = strlen(b);
j = 0;
for (i = n2 - 1;i >= 0 ; i --)
num2[j++] = b[i] - '0';
for (i=0;i < n2; i++ )
{
for (j=0; j<n1; j++)
result[i+j] += num2[i]*num1[j];
}
for( i = 0; i < MAX_LEN * 2; i ++ ) {
if (result[i] >= 10)
{
result[i+1] += result[i] / 10;
result[i] %= 10;
}
}
bool isBeginZero = false;
j=0;
for (i=n1+n2-1; i>=0; i--)
if (isBeginZero)
c[j++]=result[i]+'0';
else if (result[i]!=0)
{
c[j++]=result[i]+'0';
isBeginZero = true;
}
if (!isBeginZero) c[j++]='0';
c[j]='\0';
}
void insertPoint(char s[],int pos,int n)
{
int len,i,j;
if (pos==0) return;
len = strlen(s);
if (len<=pos*n) // 乘积全为小数部分
{
s[pos*n+1]='\0';
for (i=len-1,j=pos*n;i>=0;i--,j--)
s[j]=s[i];
for (i=j;i>0;i--)
s[i]='0';
s[0]='.';
}
else // 小数点位于乘积中间
{
s[len+1]='\0';
for (i=len,j=1; j<=pos*n; i--,j++)
s[i]=s[i-1];
s[i]='.';
}
for (i=strlen(s)-1; i>=0; i--)
{
if (s[i]=='0')
s[i] ='\0';
else
break;
}
if (s[strlen(s)-1]=='.') s[strlen(s)-1]='\0';
}
int main()
{
char s[MAX_LEN],result[2*MAX_LEN];
int n,i,flag,pos,len;
while(scanf("%s%d",s,&n)!=EOF)
{
flag = 0;
len = strlen(s);
pos=0;
for (i=0; i<len;i++) // 寻找小数点位置,并去掉小数点
{
if(s[i]=='.')
{
flag = 1;
pos = len - i - 1;
}
s[i] = s[i+flag];
}
strcpy(result,s);
for (i=1;i<n;i++)
bigNumMul(result,s,result);
insertPoint(result,pos,n);
printf("%s\n",result);
}
return 0;
}
【例3】The Idiot of the Year Contest! (POJ 3331)。
Description
There is just one basic rule in the Idiot of the Year Contest (IYC)! The contestant picks a random digit between 0 and 9, computes the factorial of the day of the year he/she is born, and counts the how many times the digit picked appears in the factorial. The contestant with highest count is the Idiot of the Year! For example, if you are born on 5th of Mordad which is the 129th day of the year, and you pick the digit 6, your score will be the number of times the digit 6 appears in 129! (that is 1 × 2 × 3 × ... × 129).
The chief judge of IYC wants you to write a program to get an integer which is the day of the year a contestant is born on and a digit and report the number of times the digit appears in the factorial of the first number.
Input
The first line of the input contains a single integer T which is the number of test cases, followed by T lines each containing the data for a test case having two numbers. The first number is the day of the year a contestant is born and the second one is the digit he/she has picked.
Output
The output contains T lines, each having one integer which is the number of times the digit appears in the factorial of the first number.
Sample Input
2
5 2
7 0
Sample Output
1
2
(1)编程思路。
设输入两个整数day和d,求day的阶乘中有多少个数字d。由于day!可能是一个非常大的数,因此采用大整数乘法。调用例1中的函数void bigNumMul(char a[],int b,char c[])即可。
(2)源程序。
#include <stdio.h>
#include <string.h>
#define MAX_LEN 1001
void bigNumMul(char a[],int b,char c[])
{
int i,j,n1,n2,t;
int num[MAX_LEN]={0},result[MAX_LEN+10]={0};
// 将a和b中存储的字符串形式的整数转换到num1和num2中去,
// num1[0]对应于个位、num1[1]对应于十位、……
n1 = strlen(a);
j = 0;
for (i = n1 - 1;i >= 0 ; i --)
num[j++] = a[i] - '0';
n2 =0;
t=b;
do {
n2++;
t=t/10;
} while (t!=0);
for (i=0;i < n1; i++)
result[i] = num[i]*b;
// 统一处理进位问题
for (i = 0; i < n1+n2; i++)
{
if (result[i] >= 10)
{
result[i+1] += result[i] / 10;
result[i] %= 10;
}
}
bool isBeginZero = false;
j=0;
for (i=n1+n2-1; i>=0; i--)
if (isBeginZero)
c[j++]=result[i]+'0';
else if (result[i]!=0)
{
c[j++]=result[i]+'0';
isBeginZero = true;
}
if (!isBeginZero) c[j++]='0';
c[j]='\0';
}
int main()
{
char a[MAX_LEN];
int t,day,digit,i,cnt;
scanf("%d",&t);
while (t--)
{
scanf("%d%d",&day,&digit);
a[0]='1', a[1]='\0';
for (i=2;i<=day;i++)
bigNumMul(a,i,a);
cnt=0;
for (i=0;a[i]!='\0';i++)
if (a[i]==digit+'0') cnt++;
printf("%d\n",cnt);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号