最后一个非零数字（POJ 1604、POJ 1150、POJ 3406）
POJ中有些问题给出了一个长数字序列（即序列中的数字非常多），这个长数字序列的生成有一定的规律，要求求出这个长数字序列中某个位上的数字是多少。这种问题通过分析，找出规律就容易解决。
例如，N!是一个非常大的数，其末尾有很多个0，如何求得其最后一个非零的数字？
-
N！的最后一个非零的数字
【例1】Just the Facts （POJ 1604）
Description
The expression N!, read as "N factorial," denotes the product of the first N positive integers, where N is nonnegative. So, for example,
N N!
0 1
1 1
2 2
3 6
4 24
5 120
For this problem, you are to write a program that can compute the last non-zero digit of any factorial for (0 <= N <= 10000). For example, if your program is asked to compute the last nonzero digit of 5!, your program should produce "2" because 5! = 120, and 2 is the last nonzero digit of 120.
Input
Input to the program is a series of nonnegative integers not exceeding 10000, each on its own line with no other letters, digits or spaces. For each integer N, you should read the value and compute the last nonzero digit of N!.
Output
For each integer input, the program should print exactly one line of output. Each line of output should contain the value N, right-justified in columns 1 through 5 with leading blanks, not leading zeroes. Columns 6 - 9 must contain " -> " (space hyphen greater space). Column 10 must contain the single last non-zero digit of N!.
Sample Input
1
2
125
3125
9999
Sample Output
1 -> 1
2 -> 2
125 -> 8
3125 -> 2
9999 -> 8
（1）编程思路1。
将N！求出来后再求最后一个非零数字是不可取的，因为10000！是个非常大的数。
实际上，由于问题只需求得N！的最后一个非零的数字，因此在计算过程中，乘积结果末尾的0全部舍弃不会影响最后求得的结果。因为在循环计算阶乘，将上一次的乘积乘以下一个数时，上一次乘积末尾的0会全部加在下一次乘积的后面。另外，由于并不需要求出这个阶乘的值，只需得到最后一个非零的数字。因此每次相乘时，无需将舍弃掉末尾0后的乘积结果全部用来相乘（这样很容易产生溢出），而只需截取乘积结果后面几位进行下一步运算即可。
注意，不能只保留最后一个非零的数字进行下一步运算。给两个简单的例子，14*15=210，而4*5=20。一个结果是1，另一个是2。125*18=2250，125*8=1000，25*8=200。32位整型数据可达到10位，而阶乘计算时的下一个数最多4 位，因此乘积结果截取舍弃掉末尾0后的后5位即可。小于5位不行，读者可以自己提交程序给POJ评判。
由于在计算N！时，（N-1）！已经求出。因此可以在计算阶乘的过程中（循环i从2~10000），不断将当前i的阶乘的最后一个非零的数字保存到ans[i]中，构造好答案表。这样，问题的求解就变成查表了。
（2）源程序1。
#include <iostream>
using namespace std;
int main()
{
int i,p,num;
int ans[10001];
ans[0]=ans[1]=1;
p=1;
for (i = 2; i <=10000; i++) // 构造答案表
{
p *= i;
while (p%10 == 0) // 去掉乘积末尾的0
p=p/10;
p %= 100000;
ans[i] = p % 10; // 得出结果
}
while (cin >> num)
{
printf("%5d -> %d\n", num, ans[num]);
}
return 0;
}
（3）编程思路2。
下面换一个思路来求得N！的最后一个非0的数字。由于质因数2和5组合之后会使得N！末尾产生0。因此，可以将1~N序列中的质因数2和5全部去掉（当然2的个数比5的个数要多，所以需在最后考虑多余的2对末位的影响）。例如，计算10！的最后一个非0的数字，将1*2*3*4*5*6*7*8*9*10序列中去掉2、5 因子后，就是1*1*3*1*1*3*7*1*9*1（去掉的因子2有8个，5有2个）。由于2、5因子已经被去除，那么剩下的数的末位数字一定是1、3、7、9中四者之一。然后再求出这么一串数末位相乘以后的末位数字是7，最后再补上6个2（末位为4）对末位的影响，得到结果8。
因此，按这种思路求解的关键是求得1~N序列中质因数2和5的个数，分别去掉2和5因子后的N个数中末位数字分别是3、7、9的数的个数。由于N!是在（N-1）！的基础上乘以N，因此，在统计N！的情况时可以在（N-1）的基础上进行。
可定义一个二维数组int table[10][10001]，其中元素table[2][n]和table[5][n]分别表示在n！中质因子2和5的个数，table[3][n]、table[7][n]和table[9][n]分别表示在1~n这n个数（分别去掉了2和5因子）中末位数字为3、7、9的数的个数。其余的的数组元素不用即可。
由于只需考虑2、5因子个数和末位3、7、9的个数这5种情况，二维数组table[10][10001]有一半的元素没有使用，为节省存储空间，可以定义数组为int table[5][10001]，其中元素table[0][n]表示在n！中质因子2的个数，table[2][n]（即table[(5-1)/2]）t表示在n！中质因子5的个数，able[1][n]、table[3][n]和table[4][n]分别表示在1~n这n个数（分别去掉了2和5因子）中末位为3、7、9的数的个数。设数字为i，则这三种情况可以统一表示为table[(i-1)/2]。
数组table的值预先求好后，N！的最后一个非0的数字就容易求得了，只需求得table[0][n]-table[2][n]个2（质因子2比5多的个数）、table[1][n]个3、table[3][n]个7和table[4][n]个9相乘所产生的末位数字即可。
实际上，末位数字为2、3、7、9的数的n次方的末位数字是有规律的，周期可统一为4。例如，2的n次方的末位数字依次为2、4、8、6、2、4、8、6、…；3的n次方的末位数字依次为3、9、7、1、3、9、7、1、…；7的n次方的末位数字依次为7、9、3、1、…；9的n次方的末位数字依次为9、1、9、1、…。因此，可以定义一个二维数组
int last[4][4] ={{6,2,4,8},{1,3,9,7},{1,7,9,3},{1,9,1,9}};
用于保存数字2、3、7、9的末位数字的循环出现情况，这样k个2、3、7、9相乘产生的末位直接查表就可以了。例如，19个3相乘产生的末位数字为last[1][19%4]=last[1][3]=7。要注意一个特殊情况，0个2的末位为1。
（4）源程序2。
#include<iostream>
using namespace std;
int main()
{
int table[5][10001],i,t,n,cnt2,cnt5,cnt3,cnt7,cnt9;
int last[4][4] ={{6,2,4,8},{1,3,9,7},{1,7,9,3},{1,9,1,9}};
table[0][1]=table[1][1]=table[2][1]=table[3][1]=table[4][1]=0;
for (i=2;i<=10000;i++)
{
t=i;
cnt2=cnt5=0;
while (t%2==0)
{
cnt2++;
t=t/2;
}
while (t%5==0)
{
cnt5++;
t=t/5;
}
table[0][i]=table[0][i-1]+cnt2; // 因子2的个数
table[2][i]=table[2][i-1]+cnt5; // 因子5的个数
table[1][i]=table[1][i-1]; // 末位数字为3的个数
table[3][i]=table[3][i-1]; // 末位数字为7的个数
table[4][i]=table[4][i-1]; // 末位数字为9的个数
if (t%10!=1)
table[(t%10-1)/2][i]++;
}
while (cin>>n)
{
cnt2=table[0][n]-table[2][n];
if (cnt2==0)
cnt2 = 1;
else
cnt2=last[0][cnt2%4];
cnt3=last[1][table[1][n]%4];
cnt7=last[2][table[3][n]%4];
cnt9=last[3][table[4][n]%4];
printf("%5d -> %d\n", n, cnt2 * cnt3 * cnt7 * cnt9 % 10);
}
return 0;
}
-
排列数P（n，m）的最后一个非0数字
【例2】The Last Non-zero Digit （POJ 1150）
Description
In this problem you will be given two decimal integer number N, M. You will have to find the last non-zero digit of the P（N，M）.This means no of permutations of N things taking M at a time.
Input
The input contains several lines of input. Each line of the input file contains two integers N (0 <= N<= 20000000), M (0 <= M <= N).
Output
For each line of the input you should output a single digit, which is the last non-zero digit of P（N，M）. For example, if P（N，M） is 720 then the last non-zero digit is 2. So in this case your output should be 2.
Sample Input
10 10
10 5
25 6
Sample Output
8
4
2
（1）编程思路。
有了例1的思路2的解决方法，求排列数P（n，m）的最后一个非0数字就变得十分容易了。
由于P(n，m) = n!/(n-m)!，就是求乘积(n-m+1)*(n-m+2)*…*(n-m+m-1)*n。因此，可以先求出1~n序列和1~(n-m)序列中质因数2、5的个数和末位数字3、7、9分别出现的次数，然后再各自相减后计算排列P(n，m)的最后一个非0数字。
但在计算排列P(n，m)的最后一个非0数字时要特别注意一个小“陷阱”：因子2出现的次数可能小于5出现的次数，例如排列数P(26,2)=26*25，因子2的个数为1、因子5的个数为2。这种情况下，最后一个非0数字一定是5，因为5乘以任何一个奇数的末位数字总是5。此时，可以直接输出5。
按照编程思路，如果直接改造例1中的源程序2，需要对数组的定义方式进行修改。因为0 <= N<= 20000000，所以数组空间应为int table[5][ 20000001]，定义静态数组的话，在栈空间进行存储分配，会造成栈的溢出，程序不能运行。修改数组的定义为动态数组，从而在堆空间进行存储分配。二维动态数组的定义方式为：
int **table=new int *[5]; // 动态申请二维数组的第一维
for(i=0;i<=5;i++)
table[i]=new int [20000001]; // 动态申请二维数组的第二维
（2）评测结果显示为“Memory Limit Exceeded”的源程序1。
#include<iostream>
using namespace std;
int main()
{
int i,t,n,m,cnt2,cnt5,cnt3,cnt7,cnt9;
int last[4][4] ={{6,2,4,8},{1,3,9,7},{1,7,9,3},{1,9,1,9}};
int **table=new int *[5]; // 动态申请二维数组的第一维
for(i=0;i<=5;i++)
table[i]=new int [20000001]; // 动态申请二维数组的第二维
table[0][0]=table[1][0]=table[2][0]=table[3][0]=table[4][0]=0;
for (i=1;i<=20000000;i++)
{
t=i;
cnt2=cnt5=0;
while (t%2==0)
{
cnt2++;
t=t/2;
}
while (t%5==0)
{
cnt5++;
t=t/5;
}
table[0][i]=table[0][i-1]+cnt2; // 因子2的个数
table[2][i]=table[2][i-1]+cnt5; // 因子5的个数
table[1][i]=table[1][i-1]; // 末位数字为3的个数
table[3][i]=table[3][i-1]; // 末位数字为7的个数
table[4][i]=table[4][i-1]; // 末位数字为9的个数
if (t%10!=1)
table[(t%10-1)/2][i]++;
}
while (cin>>n>>m)
{
if (m == 0)
{
cout<<"1"<<endl;
continue;
}
cnt2=table[0][n]-table[0][n-m];
cnt5=table[2][n]-table[2][n-m];
if (cnt2>=cnt5)
{
cnt2=cnt2-cnt5;
if (cnt2==0)
cnt2 = 1;
else
cnt2=last[0][cnt2%4];
cnt3=last[1][(table[1][n]-table[1][n-m])%4];
cnt7=last[2][(table[3][n]-table[3][n-m])%4];
cnt9=last[3][(table[4][n]-table[4][n-m])%4];
cout<<cnt2 * cnt3 * cnt7 * cnt9 % 10<<endl;
}
else
cout<<5<<endl;
}
return 0;
}
上面的源程序能正确运行，也可以正确得到结果。但将其提交给POJ测评系统，不能“Accepted”，评测结果显示为“Memory Limit Exceeded”，主要是动态数组分配超出了内存限制。因此，不能采用数组的方式来保存1~N序列中数字2、3、5、7、9的相关情况。如果对于每组测试数据，都采用循环计算序列n-m+1~n之间各数字中质因子2、5的个数及末位为3、7、9的个数，可编写如下的程序2。
（3）评测结果显示为“Time Limit Exceeded”的源程序2。
#include<iostream>
using namespace std;
int main()
{
int i,t,n,m,cnt2,cnt5,cnt3,cnt7,cnt9;
int last[4][4] ={{6,2,4,8},{1,3,9,7},{1,7,9,3},{1,9,1,9}};
while (cin>>n>>m)
{
if (m == 0)
{
cout<<"1"<<endl;
continue;
}
cnt2=cnt3=cnt5=cnt7=cnt9=0;
for (i=n-m+1;i<=n;i++)
{
t=i;
while (t%2==0)
{
cnt2++;
t=t/2;
}
while (t%5==0)
{
cnt5++;
t=t/5;
}
if (t%10==3) cnt3++;
else if (t%10==7) cnt7++;
else if (t%10==9) cnt9++;
}
if (cnt2>=cnt5)
{
cnt2=cnt2-cnt5;
if (cnt2==0)
cnt2 = 1;
else
cnt2=last[0][cnt2%4];
cnt3=last[1][cnt3%4];
cnt7=last[2][cnt7%4];
cnt9=last[3][cnt9%4];
cout<<cnt2 * cnt3 * cnt7 * cnt9 % 10<<endl;
}
else
cout<<5<<endl;
}
return 0;
}
上面的源程序也能正确运行，并正确得到结果。但将其提交给POJ测评系统，仍不能“Accepted”，评测结果显示为“Time Limit Exceeded”。因为对每组测试数据，都采用循环for (i=n-m+1;i<=n;i++)来处理数字2、5、3、7、9的相关情况，造成超时。因此需要找到一种快速求出1~n这n个数中质因子2和5的个数，以及分别去掉2和5因子后的N个数中末位数字分别是3、7、9的数的个数。
（4）快速求解的思路。
先看怎样快速求序列1~n这n个数中质因子2的个数。将n个数按除以2的余数为1或0可以分成两个子序列，即一个奇数序列（有(n+1)/2个数）和一个偶数序列（有n/2个数）。奇数序列中不含质因子2，偶数序列中每个数均至少含有一个因子2，即序列中质因子2的个数至少为n/2个，将序列中每个数均除以2，得到一个1~n/2的子序列；重复这个处理过程，直到序列为空。因此，统计1~n这n个数中因子2的个数cnt可以写成如下的循环：
int cnt=0;
while(n)
{
cnt+=n/2;
n/=2;
}
同理，统计1~n这n个数中因子5的个数cnt也可以写成这样的循环。因为，将n个数按除以5的余数为4、3、2、1或0可以分成5个子序列，其中只有余数为5的序列（有n/5个数）中含有质因子5。这个序列中每个数均至少含有一个因子2，即序列中质因子5的个数至少为n/5个，将序列中每个数均除以5，可得到一个1~n/5的子序列。
再来看怎样快速统计序列中末位数字为3、7、9的数的个数。
设用函数getLast(n,x)表示在1~n这n个数中，末位数字为奇数x的数的个数。
一个1~n的数字序列可以奇偶特性分成两个子序列。例如，1~10的序列可分成子序列1{1，3，5，7，9}和子序列2 {2，4，6，8，10}。可以对两个子序列分别进行统计。
子序列1由小于等于n的奇数组成，设函数getOdd(n,x)表示小于等于n的奇数中末位数字为奇数x的数的个数。而子序列2中的每个数除以2后，得到一个从1~n/2的子序列。例如，{2，4，6，8，10}中的每个数除以2，就是序列{1，2，3，4，5}，也就是说这个问题可看成一个原来问题的子问题。
由此，可得到递推式getLast(n,x) = getLast(n/2,x) +getOdd(n,x)。
getOdd(n,x)怎么求呢？观察小于等于n的奇数序列（有n/2个数）。按末位数字分成5组{1,11,21,31，…}，{3,13,23,33，…}，{5,15,25,35，…}，{7,17,27,37，…}，{9,19,29,39，…}，每组至少有n/10个数。由于n不一定是10的倍数，还需看看n%10>=x是否成立，成立就加1，不成立就不加1。在这5组中，末位数字为5的组中每个数都含有质因子5，要去掉5这个因子，每个数除以5后，序列又变成了{1,3,5,7,…}，该序列中n/10个数奇数，所有的奇数小于等于n/5，也就是说这个问题也看看成一个原来问题的子问题。
由此，可得到递推式 getOdd(n,x)=n/10+(n%10>=x)+getOdd(n/5,x)。
有了上面这两个递推式，采用递归的方法能很快求得1~n序列中末位数字为3、7、9的数的个数。
（5）可Accepted的源程序3。
#include <iostream>
using namespace std;
int getFactor(int n,int k)
{
int cnt=0;
while(n)
{
cnt+=n/k;
n/=k;
}
return cnt;
}
int getOdd(int n,int k)
{
if (n==0) return 0;
return n/10+(n%10>=k)+getOdd(n/5,k);
}
int getLast(int n,int k)
{
if (n==0) return 0;
return getLast(n/2,k)+getOdd(n,k);
}
int main()
{
int n,m,cnt2,cnt5,cnt3,cnt7,cnt9;
int last[4][4] ={{6,2,4,8},{1,3,9,7},{1,7,9,3},{1,9,1,9}};
while (cin>>n>>m)
{
if (m == 0)
{
cout<<"1"<<endl;
continue;
}
cnt2 = getFactor(n,2) - getFactor(n-m,2);
cnt5 = getFactor(n,5) - getFactor(n-m,5);
cnt3 = getLast(n,3) - getLast(n-m,3);
cnt7 = getLast(n,7) - getLast(n-m,7);
cnt9 = getLast(n,9) - getLast(n-m,9);
if (cnt2>=cnt5)
{
cnt2=cnt2-cnt5;
if (cnt2==0)
cnt2 = 1;
else
cnt2=last[0][cnt2%4];
cnt3=last[1][cnt3%4];
cnt7=last[2][cnt7%4];
cnt9=last[3][cnt9%4];
cout<<cnt2 * cnt3 * cnt7 * cnt9 % 10<<endl;
}
else
cout<<5<<endl;
}
return 0;
}
-
组合数C(m,n)的最后一个非0数字
在理解了上述编程思路后，可以继续尝试解决POJ 3406问题“Last digit”。即输入整数n和m （1000000≥n≥m≥1），求组合数C(m,n)的最后一个非0数字。
.
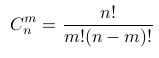将上面的“可Accepted的源程序3”的main函数改写为：
int main()
{
int last[4][4] ={{6,2,4,8},{1,3,9,7},{1,7,9,3},{1,9,1,9}};
int n,m,res=1,cnt2,cnt3,cnt5,cnt7,cnt9;
cin>>n>>m;
cnt2 = getFactor(n,2) - getFactor(n-m,2)- getFactor(m,2);
cnt5 = getFactor(n,5) - getFactor(n-m,5)- getFactor(m,5);
cnt3 = getLast(n,3) - getLast(n-m,3)- getLast(m,3);
cnt7 = getLast(n,7) - getLast(n-m,7)- getLast(m,7);
cnt9 = getLast(n,9) - getLast(n-m,9)- getLast(m,9);
if(cnt2<cnt5) res*=5;
else if(cnt2>cnt5) res*=last[0][(cnt2-cnt5)%4];
res*=last[1][(cnt3%4+4)%4]; // 考虑负数时的正向取模
res*=last[2][(cnt7%4+4)%4];
res*=last[3][(cnt9%4+4)%4];
cout<<res%10<<endl;
return 0;
}
提交给POJ网站，评判程序显示结果“Accepted”。
