数据结构第四节(树(中))
树
这次接着整树,上次说了树的基本性质和遍历一颗树的4种方式,这次会实现几种很“有用”的二叉树
二叉搜索树
对一颗二叉树,该如何实现它的动态查找(查找的同时会有新元素的添加,以及对已包含的元素的删除),前面已经学过了二分查找,很自然的想到如果在构建一棵树时,使得所有节点的左子树都比他小,右子树都比他大,对这样的树,叫做二叉搜索树。根据这样的性质,可以很自然的得出,二叉搜索树最小的节点它的最左端的节点,二叉搜索树最大的节点它的最右端的节点。
二叉搜索树的查找
对于一棵二叉搜索树,他任何节点的左子树都比他小,右子树都比他大,很自然的可以实现二分查找,从根结点开始遍历,如果当前节点比需要查找的值大从他的右子树,比需要查找的值小从他的左子树,相等则返回。如果直到指向为空都无法找到,说明该节点并不在树上,下面是代码实现。
//find max value
Position FindMax(BinTree BST) {
if (!BST) {
return NULL;
}
while (BST->Right) {
BST = BST->Right;
}
return BST;
}
//find min value
Position FindMin(BinTree BST) {
if (!BST) {
return NULL;
}
while (BST->Left) {
BST = BST->Left;
}
return BST;
}
//find in value
Position Find(BinTree BST, ElementType X) {
//the tree is empty ,return NULL;
while (BST) {
//the X is big than now position's value, may be in the right or doesn't has.
if (X > BST->Data) {
BST = BST->Right;
}
else if (X < BST->Data) {
BST = BST->Left;
}
else {
return BST;
}
}
return NULL;
}
二叉搜索树的插入
同查找数值一样,对于二叉搜索树的插入,先从根结点开始遍历,如果小于它就插入它的左子树,大于它就插入它的右子树。直到找到了位置,再申请一个节点将它接上去。
//insert
BinTree Insert(BinTree BST, ElementType X) {
//if the tree is empty,creat a node and return
if (!BST) {
BST = malloc(sizeof(struct TNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
}
else {
//the X is big than now position, insert X in its right tree
if (X > BST->Data) {
BST->Right = Insert(BST->Right, X);
}
//the X is small than now position, insert X in its left tree
else if (X < BST->Data) {
BST->Left = Insert(BST->Left, X);
}
//when the X already in the tree, do nothing
else {
}
}
return BST;
}
二叉搜索树的删除
二叉树最多有两个节点,故在删除时只有三种情况,分别是该节点没有子节点(叶子节点),有一个子节点,有两个子节点。
如果没有子节点,直接释放掉该节点,返回一个NULL接上去。如果只有一个子节点,只需要释放该节点,并把他的子节点接上去即可。有两个子节点时,问题变得麻烦起来,有一个策略是,将问题转化为删除一个叶节点,或删除一个只有一个儿子的节点。
通过二叉搜索树的性质我们知道,一颗二叉搜索树的最小值,位于他的最左端,最大值位于它的最右端,对需要删除的度为2的节点,我们可以找到该节点的右子树的最小值的那个节点,赋值给该节点,同时删除掉它(因为二叉搜索树的性质,它只可能是叶节点,或者只有一个儿子,而且那样做不会破坏二叉搜索树的一个节点左子树都比他小,右子树都比他大的性质),找该节点左子树的最大值同理。
//delete
BinTree Delete(BinTree BST, ElementType X) {
if (!BST) {
printf("NOT Found\n");
}
else {
//the X is big than now position, delete X in its right tree
if (X > BST->Data) {
BST->Right = Delete(BST->Right, X);
}
//the X is small than now position, delete X in its left tree
else if (X < BST->Data) {
BST->Left = Delete(BST->Left, X);
}
//find the X positon
else {
//has two sub tree
if (BST->Left && BST->Right) {
BinTree temp = FindMax(BST->Left);
BST->Data = temp->Data;
temp->Data = X;
Delete(BST->Left, X);
}
//has one or no sub tree
else {
BinTree temp = BST;
//don't has left sub tree
if (!BST->Left) {
BST = BST->Right;
}
//don't has right sub tree
else if (!BST->Right) {
BST = BST->Left;
}
free(temp);
}
}
}
return BST;
}
平衡二叉树
平衡二叉树的性质
前面实现了二叉搜索树,现在,想象一下,如果按照升序序列将节点(1-10)插入树中,不难发现,这个树成了颗单边树,这样的树有着和链表一样的查找效率,肯定是不希望发生这样的事情的,这里引入一个叫平衡二叉树的树(AVL),那么这种树有什么特点呢?
平衡二叉树由二叉搜索树而来,同样的,也是必须满足BST的性质,而且,这颗树必须满足,所有节点的左右子树高度差BF(T)=\(h_l\)-\(h_r\)不大于1.
考虑一下,一个n层高的平衡二叉树最小需要几个节点?
答案是\(a_n\)=\(1+a_(n-1)+a_(n-2)\)
对于一层高的平衡二叉树,需要一个节点,两层高的需要两个节点,三层高的则需要一个节点加上它的左子树(两层的平衡二叉树)和他的右子树一层的平衡二叉树。整个是一个递归的过程
平衡二叉树的调整
为了保证平衡二叉树的性质,我们再插入节点或者删除节点时,使该树不平衡时,又应该如何调整它使它平衡呢?根据上面平衡二叉树是一个递归的生成过程,我们可以知道,对于插入或者删除,只需要修正被破坏平衡的节点为根节点构成的树,即修正整棵树的平衡。
第一种情况,破坏了平衡的节点,位于被破坏平衡节点的右子树的右子树,此时将被破坏平衡节点的右儿子提起来,自己做右儿子的左儿子,将右儿子的左儿子做自己的右儿子。(RR旋转)
第二种情况,破坏了平衡的节点,位于被破坏平衡节点的左子树的左子树,根据对称性我们很容易想到,此时将被破坏平衡节点的左儿子提起来,自己做左儿子的右儿子,将左儿子的右儿子做自己的左儿子。(LL旋转)
第三种情况,破坏了平衡的节点,位于被破坏平衡节点的左子树的右子树,此时将破坏平衡节点的所在树的根节点提出来做新的根,并令该根的左儿子为原树根的左儿子,右儿子为原树根节点。并且把破坏平衡节点的所在树的根节点的左右子树,分别接在当前根节点左儿子的右边和右儿子的左边。(LR旋转)
第四种情况,类似于第3种情况的对称,破坏了平衡的节点,位于被破坏平衡节点的右子树的左子树,只需对称着像第三种情况那样做。(RL旋转)
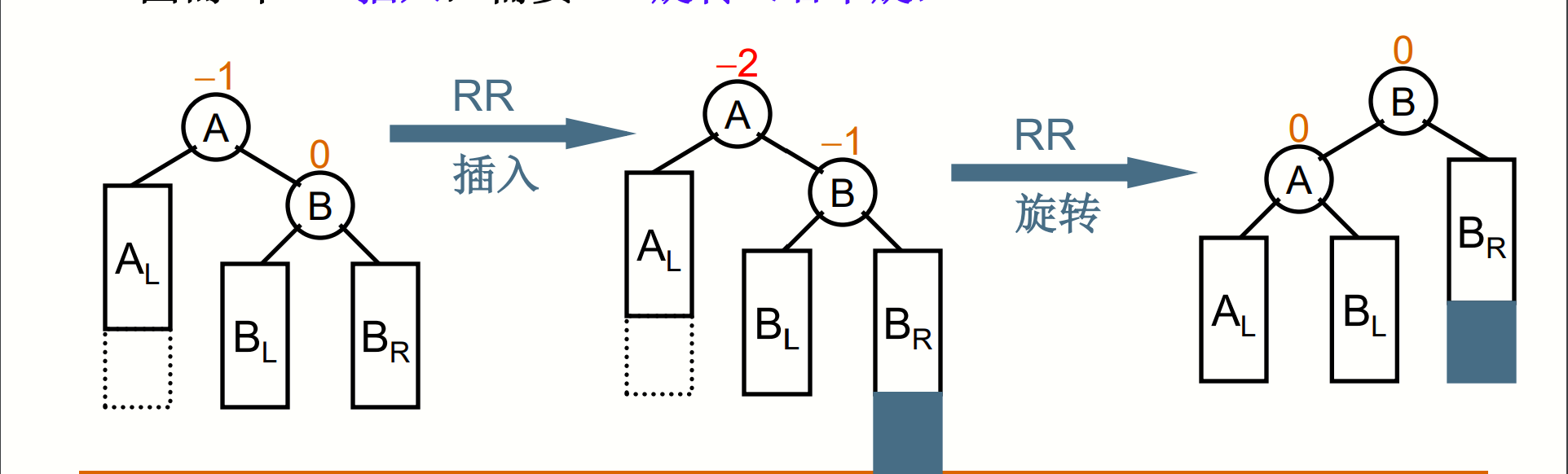
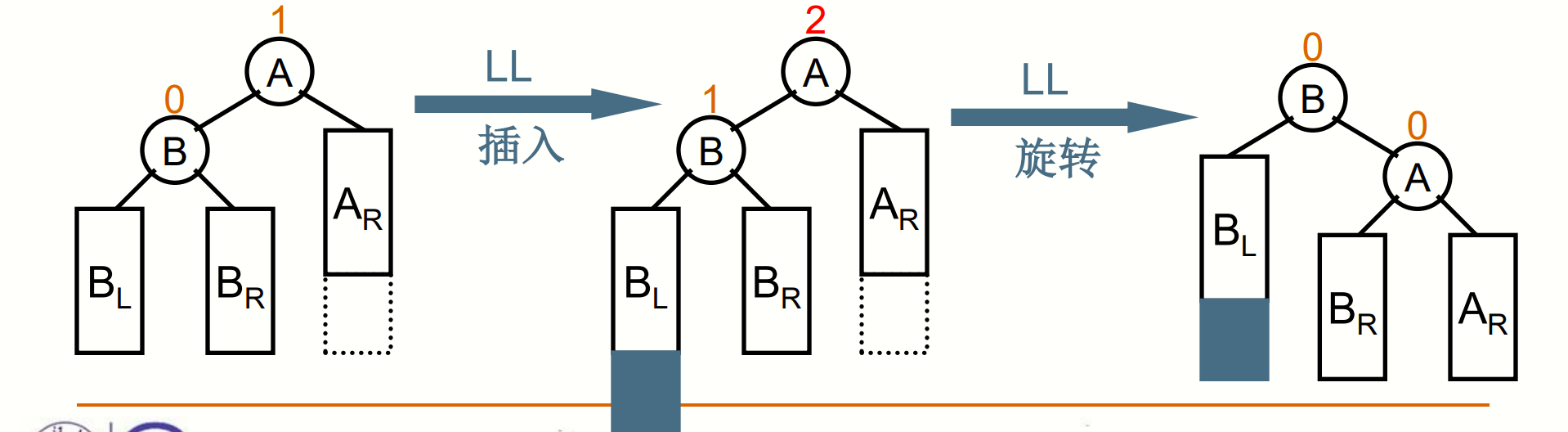
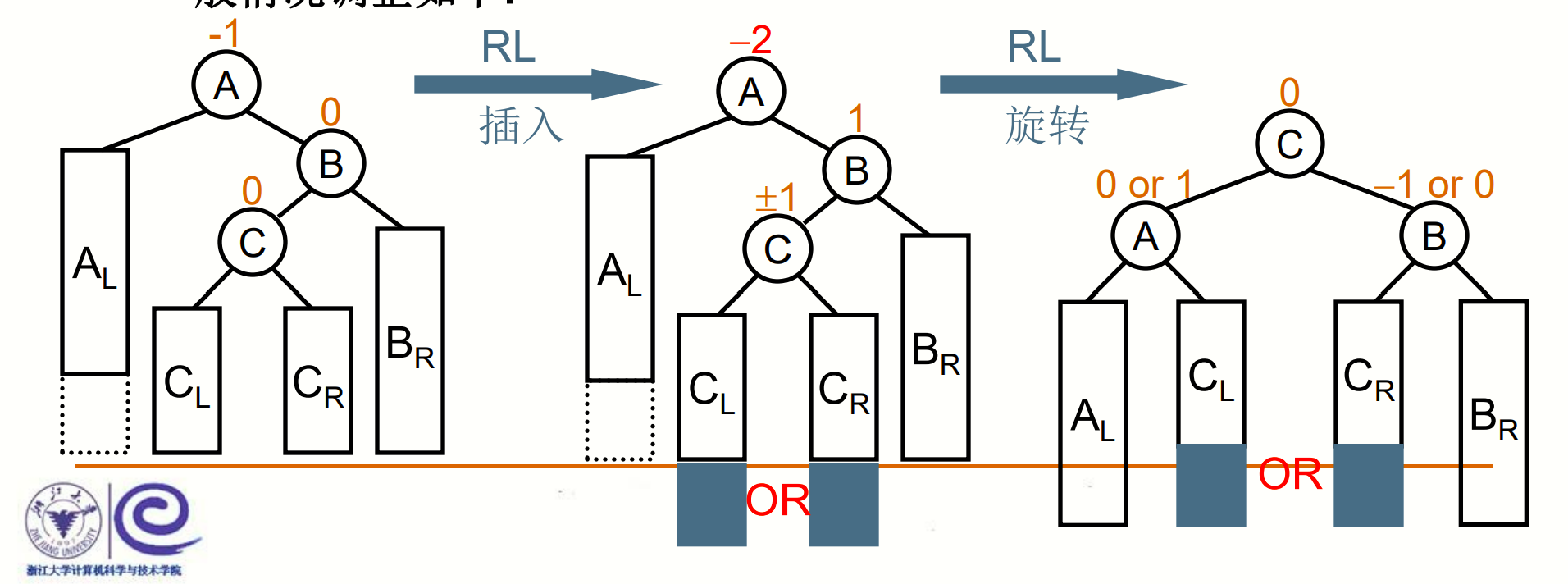
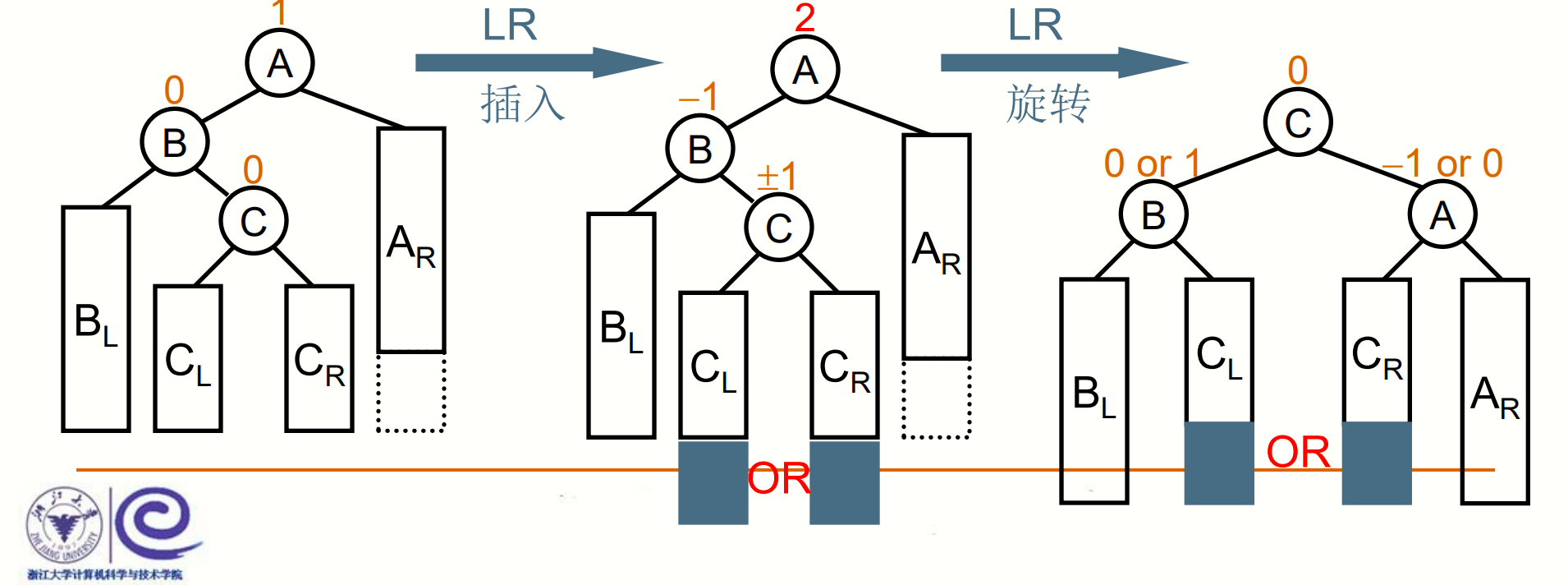
图片来自中国MOOC大学 数据结构—— 来源
下面的代码给出了插入操作时的调整,查看代码可以发现插入操作可以分为两步,第1步是按照二叉搜索树的插入方式,先将其插入到树中。第2步是判断插入节点后,这棵树是否还平衡。同理对于删除操作时,第1步按照二叉搜索树的删除方式,将需要删除的节点删除,第2步是检查树是否还平衡。
#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
typedef struct TreeNode* BinTree;
#define ElementType int
struct TreeNode
{
ElementType Data;
BinTree Left;
BinTree Right;
int Height;
};
int getHeight(BinTree T) {
if (T->Left == NULL && T->Right == NULL) {
return 1;
}
else if (T->Left != NULL && T->Right == NULL) {
return T->Left->Height+1;
}
else if (T->Left == NULL && T->Right != NULL) {
return T->Right->Height + 1;
}
else {
return max(T->Left->Height, T->Right->Height)+1;
}
}
BinTree RR(BinTree T) {
BinTree right = T->Right;
T->Right = right->Left;
right->Left = T;
right->Height = getHeight(right);
T->Height = getHeight(T);
return right;
}
BinTree LL(BinTree T) {
BinTree left = T->Left;
T->Left = left->Right;
left->Right = T;
left->Height = getHeight(left);
T->Height = getHeight(T);
return left;
}
BinTree LR(BinTree T) {
T->Left = RR(T->Left);
return LL(T);
}
BinTree RL(BinTree T) {
T->Right = LL(T->Right);
return RR(T);
}
//insert
BinTree Insert(BinTree BST, ElementType X) {
//if the tree is empty,creat a node and return
if (!BST) {
BST = (BinTree)malloc(sizeof(struct TreeNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
BST->Height = 0;
}
else {
//the X is big than now position, insert X in its right tree
if (X > BST->Data) {
BST->Right = Insert(BST->Right, X);
int h1, h2;
if (BST->Left == NULL) {
h1 = 0;
}
else {
h1 = BST->Left->Height;
}
if (BST->Right == NULL) {
h2 = 0;
}
else {
h2 = BST->Right->Height;
}
//the tree is not avl
if (abs(h1-h2)==2) {
//LL
if (X < BST->Right->Data) {
BST = RL(BST);
}
//LR
else {
BST = RR(BST);
}
}
}
//the X is small than now position, insert X in its left tree
else if (X < BST->Data) {
BST->Left = Insert(BST->Left, X);
int h1, h2;
if (BST->Left == NULL) {
h1 = 0;
}
else {
h1 = BST->Left->Height;
}
if (BST->Right == NULL) {
h2 = 0;
}
else {
h2 = BST->Right->Height;
}
if (abs(h1-h2) == 2) {
//RR
if (X > BST->Left->Data) {
BST = LR(BST);
}
//RL
else {
BST = LL(BST);
}
}
}
//when the X already in the tree, do nothing
else {
}
}
BST->Height = getHeight(BST);
return BST;
}
课后练习题(4个小题)
04-树4 是否同一棵二叉搜索树 (25point(s))
给定一个插入序列就可以唯一确定一棵二叉搜索树。然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。于是对于输入的各种插入序列,你需要判断它们是否能生成一样的二叉搜索树。
输入格式:
输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L,分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数,作为初始插入序列。最后L行,每行给出N个插入的元素,属于L个需要检查的序列。
简单起见,我们保证每个插入序列都是1到N的一个排列。当读到N为0时,标志输入结束,这组数据不要处理。
输出格式:
对每一组需要检查的序列,如果其生成的二叉搜索树跟对应的初始序列生成的一样,输出“Yes”,否则输出“No”。
输入样例:
4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0
输出样例:
Yes
No
No
解法:模拟法,将默认树读入保存,每次读入生成一个新树,再递归去判断每个节点位置是否相同,不同返回false,相同返回判断左右两个子树是否相同的合取运算,如果传入的两个树都空,返回true,其中一个不空返回false,都不空再去判断
代码实现:
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef struct TreeNode* BinTree;
#define ElementType int
struct TreeNode
{
ElementType Data;
BinTree Left;
BinTree Right;
};
//insert
BinTree insert(ElementType X, BinTree BST) {
//if the tree is empty,creat a node and return
if (!BST) {
BST = (BinTree)malloc(sizeof(struct TreeNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
}
else {
//the X is big than now position, insert X in its right tree
if (X > BST->Data) {
BST->Right = insert(X, BST->Right);
}
//the X is small than now position, insert X in its left tree
else if (X < BST->Data) {
BST->Left = insert(X, BST->Left);
}
//when the X already in the tree, do nothing
else {
}
}
return BST;
}
bool check(BinTree T1, BinTree T2) {
if (T1==NULL && T2==NULL) {
return true;
}
if(T1->Data==T2->Data){
return check(T1->Left, T2->Left)&&check(T1->Right, T2->Right);
}
return false;
}
int main()
{
int n, l;
while (scanf("%d", &n)) {
if (n == 0) {
break;
}
scanf("%d", &l);
BinTree OT = NULL;
for (int i = 0; i < n; i++) {
int temp;
scanf("%d", &temp);
OT = insert(temp, OT);
}
for (int j = 0; j < l; j++) {
BinTree TestTree = NULL;
for (int i = 0; i < n; i++) {
int temp;
scanf("%d", &temp);
TestTree = insert(temp, TestTree);
}
if (!check(OT, TestTree)) {
printf("No\n");
}
else {
printf("Yes\n");
}
}
}
}
04-树5 Root of AVL Tree (25point(s))
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print the root of the resulting AVL tree in one line.
Sample Input 1:
5
88 70 61 96 120
Sample Input 1:
70
解析:题目的意思是,让你构建一颗2叉平衡树,给定你插入序列,让你输出他的根节点,emm....那就模拟做一颗AVL(思路课程已经说了,就是把代码转化成程序的过程)
代码:
#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
typedef struct TreeNode* BinTree;
#define ElementType int
struct TreeNode
{
ElementType Data;
BinTree Left;
BinTree Right;
int Height;
};
int getHeight(BinTree T) {
if (T->Left == NULL && T->Right == NULL) {
return 1;
}
else if (T->Left != NULL && T->Right == NULL) {
return T->Left->Height+1;
}
else if (T->Left == NULL && T->Right != NULL) {
return T->Right->Height + 1;
}
else {
return max(T->Left->Height, T->Right->Height)+1;
}
}
BinTree RR(BinTree T) {
BinTree right = T->Right;
T->Right = right->Left;
right->Left = T;
right->Height = getHeight(right);
T->Height = getHeight(T);
return right;
}
BinTree LL(BinTree T) {
BinTree left = T->Left;
T->Left = left->Right;
left->Right = T;
left->Height = getHeight(left);
T->Height = getHeight(T);
return left;
}
BinTree LR(BinTree T) {
T->Left = RR(T->Left);
return LL(T);
}
BinTree RL(BinTree T) {
T->Right = LL(T->Right);
return RR(T);
}
//insert
BinTree Insert(BinTree BST, ElementType X) {
//if the tree is empty,creat a node and return
if (!BST) {
BST = (BinTree)malloc(sizeof(struct TreeNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
BST->Height = 0;
}
else {
//the X is big than now position, insert X in its right tree
if (X > BST->Data) {
BST->Right = Insert(BST->Right, X);
int h1, h2;
if (BST->Left == NULL) {
h1 = 0;
}
else {
h1 = BST->Left->Height;
}
if (BST->Right == NULL) {
h2 = 0;
}
else {
h2 = BST->Right->Height;
}
//the tree is not avl
if (abs(h1-h2)==2) {
//LL
if (X < BST->Right->Data) {
BST = RL(BST);
}
//LR
else {
BST = RR(BST);
}
}
}
//the X is small than now position, insert X in its left tree
else if (X < BST->Data) {
BST->Left = Insert(BST->Left, X);
int h1, h2;
if (BST->Left == NULL) {
h1 = 0;
}
else {
h1 = BST->Left->Height;
}
if (BST->Right == NULL) {
h2 = 0;
}
else {
h2 = BST->Right->Height;
}
if (abs(h1-h2) == 2) {
//RR
if (X > BST->Left->Data) {
BST = LR(BST);
}
//RL
else {
BST = LL(BST);
}
}
}
//when the X already in the tree, do nothing
else {
}
}
BST->Height = getHeight(BST);
return BST;
}
int main(void) {
int n;
scanf("%d", &n);
BinTree BST = NULL;
for (int i = 0; i < n; i++)
{
int temp;
scanf("%d", &temp);
BST = Insert(BST, temp);
}
printf("%d\n", BST->Data);
return 0;
}
04-树6 Complete Binary Search Tree (30point(s))
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:
The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
Both the left and right subtrees must also be binary search trees.
A Complete Binary Tree (CBT) is a tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right.
Now given a sequence of distinct non-negative integer keys, a unique BST can be constructed if it is required that the tree must also be a CBT. You are supposed to output the level order traversal sequence of this BST.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤1000). Then N distinct non-negative integer keys are given in the next line. All the numbers in a line are separated by a space and are no greater than 2000.
Output Specification:
For each test case, print in one line the level order traversal sequence of the corresponding complete binary search tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.
Sample Input:
10
1 2 3 4 5 6 7 8 9 0
Sample Output:
6 3 8 1 5 7 9 0 2 4
题解:
题目的意思是给你N个数字,让你把它排成完全二叉搜索树(同时具有二差搜索树的性质和完全二叉树的性质),输出这棵树的程序遍历。仔细想一下其实根本不用构建一棵树,因为完全二叉树固定了节点的位置 ,这棵树只可能有一种形状,我们只需要将这N个数字排好序 ,递归的把它存进树组中,数组一位置为开始节点,他的儿子就是他当前位置的二倍和二倍加1。
代码实现:
#include<cstdio>
#include<algorithm>
#include<string.h>
#include<math.h>
#include<stdbool.h>
using namespace std;
int arr1[1001];
int arr[1001];
int getrootIndex(int Left,int Right) {
int p = floor(log10(Right-Left+1)/ log10(2));
int leftnum = min(pow(2,p-1), (Right - Left + 1)-(pow(2, p)-1));
return Left+leftnum+ (pow(2, p-1) - 1);
}
void specialSort(int Left,int Right,int root) {
if (Left>Right) {
return;
}
else if (Left == Right) {
arr1[root] = arr[Left];
}
else {
int p = getrootIndex(Left, Right);
arr1[root] = arr[p];
specialSort(Left, p - 1, root * 2);
specialSort(p+1, Right, root * 2+1);
}
}
int main() {
int n, t;
scanf("%d",&n);
memset(arr, 10000, sizeof(arr));
memset(arr1, 10000, sizeof(arr1));
for (int i = 0; i < n; i++)
{
scanf("%d", &t);
arr[i] = t;
}
sort(arr, arr + n);
specialSort(0, n - 1, 1);
bool isf = true;
for (int i = 1; i <= n; i++)
{
if (isf) {
printf("%d",arr1[i]);
isf = false;
}
else {
printf(" %d", arr1[i]);
}
}
return 0;
}
04-树7 二叉搜索树的操作集 (30point(s))
本题要求实现给定二叉搜索树的5种常用操作。
函数接口定义:
BinTree Insert( BinTree BST, ElementType X );
BinTree Delete( BinTree BST, ElementType X );
Position Find( BinTree BST, ElementType X );
Position FindMin( BinTree BST );
Position FindMax( BinTree BST );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
- 函数Insert将X插入二叉搜索树BST并返回结果树的根结点指针;
- 函数Delete将X从二叉搜索树BST中删除,并返回结果树的根结点指针;如果X不在树中,则打印一行Not Found并返回原树的根结点指针;
- 函数Find在二叉搜索树BST中找到X,返回该结点的指针;如果找不到则返回空指针;
- 函数FindMin返回二叉搜索树BST中最小元结点的指针;
- 函数FindMax返回二叉搜索树BST中最大元结点的指针。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
void PreorderTraversal( BinTree BT ); /* 先序遍历,由裁判实现,细节不表 */
void InorderTraversal( BinTree BT ); /* 中序遍历,由裁判实现,细节不表 */
BinTree Insert( BinTree BST, ElementType X );
BinTree Delete( BinTree BST, ElementType X );
Position Find( BinTree BST, ElementType X );
Position FindMin( BinTree BST );
Position FindMax( BinTree BST );
int main()
{
BinTree BST, MinP, MaxP, Tmp;
ElementType X;
int N, i;
BST = NULL;
scanf("%d", &N);
for ( i=0; i<N; i++ ) {
scanf("%d", &X);
BST = Insert(BST, X);
}
printf("Preorder:"); PreorderTraversal(BST); printf("\n");
MinP = FindMin(BST);
MaxP = FindMax(BST);
scanf("%d", &N);
for( i=0; i<N; i++ ) {
scanf("%d", &X);
Tmp = Find(BST, X);
if (Tmp == NULL) printf("%d is not found\n", X);
else {
printf("%d is found\n", Tmp->Data);
if (Tmp==MinP) printf("%d is the smallest key\n", Tmp->Data);
if (Tmp==MaxP) printf("%d is the largest key\n", Tmp->Data);
}
}
scanf("%d", &N);
for( i=0; i<N; i++ ) {
scanf("%d", &X);
BST = Delete(BST, X);
}
printf("Inorder:"); InorderTraversal(BST); printf("\n");
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
10
5 8 6 2 4 1 0 10 9 7
5
6 3 10 0 5
5
5 7 0 10 3
输出样例
Preorder: 5 2 1 0 4 8 6 7 10 9
6 is found
3 is not found
10 is found
10 is the largest key
0 is found
0 is the smallest key
5 is found
Not Found
Inorder: 1 2 4 6 8 9
解析:实现的函数即为本章第1节部分的内容,跟着思路写就好
代码:
//find max value
Position FindMax(BinTree BST) {
if (!BST) {
return NULL;
}
while (BST->Right) {
BST = BST->Right;
}
return BST;
}
//find min value
Position FindMin(BinTree BST) {
if (!BST) {
return NULL;
}
while (BST->Left) {
BST = BST->Left;
}
return BST;
}
//find in value
Position Find(BinTree BST, ElementType X) {
//the tree is empty ,return NULL;
while (BST) {
//the X is big than now position's value, may be in the right or doesn't has.
if (X > BST->Data) {
BST = BST->Right;
}
else if (X < BST->Data) {
BST = BST->Left;
}
else {
return BST;
}
}
return NULL;
}
//insert
BinTree Insert(BinTree BST, ElementType X) {
//if the tree is empty,creat a node and return
if (!BST) {
BST = malloc(sizeof(struct TNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
}
else {
//the X is big than now position, insert X in its right tree
if (X > BST->Data) {
BST->Right = Insert(BST->Right, X);
}
//the X is small than now position, insert X in its left tree
else if (X < BST->Data) {
BST->Left = Insert(BST->Left, X);
}
//when the X already in the tree, do nothing
else {
}
}
return BST;
}
//delete
BinTree Delete(BinTree BST, ElementType X) {
if (!BST) {
printf("Not Found\n");
}
else {
//the X is big than now position, delete X in its right tree
if (X > BST->Data) {
BST->Right = Delete(BST->Right, X);
}
//the X is small than now position, delete X in its left tree
else if (X < BST->Data) {
BST->Left = Delete(BST->Left, X);
}
//find the X positon
else {
//has two sub tree
if (BST->Left && BST->Right) {
BinTree temp = FindMax(BST->Left);
BST->Data = temp->Data;
temp->Data = X;
Delete(BST->Left, X);
}
//has one or no sub tree
else {
BinTree temp = BST;
//don't has left sub tree
if (!BST->Left) {
BST = BST->Right;
}
//don't has right sub tree
else if (!BST->Right) {
BST = BST->Left;
}
free(temp);
}
}
}
return BST;
}

