数据结构第三节(树(上))
树
树是一种基本的层次结构,相比线性结构,在动态查找上,效率更高。
在说树之前,首先先说一下线性结构中两种常用的查找方式。
两种查找方式顺序查找和二分查找
顺序查找(哨兵法)
对于一个线性表方便的查找方式是,从后向前查找且将被查找的值放在最前面作为哨兵,只需要判断下标位置的元素是否为查找元素,而不用考虑下标是否走到边界,(因为边界元素正好是我们的哨兵,走到了这里自动退出)
代码实现:
#include<stdio.h>
#include<stdlib.h>
typedef struct LNode* List;
#define MAXSIZE 100
#define ElementType int
struct LNode
{
ElementType Data[MAXSIZE];
int length;
};
int sequentailSearch(List L,ElementType key) {
int i = 0;
L->Data[0] = key;//建立哨兵
for (i = L->length; L->Data[i] != key; i--);
return i;//找到返回对应下标,没找到返回0
}
二分查找
想对一个线性表使用二分查找,他必须是有序的
例如有一个线性表从小到大排列,设置两个变量(left和right)分别设为线性表的两端下标,通过比较中间位置的值于被查找元素的值,改变2个变量的指向,如果中间的值大于被查到元素,说明被查找元素应该在中间的右侧,我们将right设为中间的位置下标减1,同理....
代码实现:
#include<stdio.h>
#include<stdlib.h>
typedef struct LNode* List;
#define MAXSIZE 100
#define ElementType int
struct LNode
{
ElementType Data[MAXSIZE];
int length;
};
//从小到大排序的情况
int binarySearch(List L, ElementType key) {
int left = 1, right = L->length;
while (left <= right) {
int mid = (left + right) / 2;
//如果mid下标的元素大于要找的,说明在left-mid之间,顾使right = mid-1。
if (L->Data[mid] > key) {
right = mid - 1;
}
else if (L->Data[mid] < key) {
left = mid + 1;
}
else {
return mid;
}
}
return -1;//查找失败返回-1
}
树
树是一种抽象数据类型或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。n = 0时为空树。
非空树的性质
1.只含有一个根节点
2.其余的节点分成多个不相交的节点哪个节点又是原树的子树
3.子树互不相交,除根节点外所有节点都有一个父节点
4.N个节点的数有N-1条边
树的一些基本术语
1.结点的度(Degree):结点的子树个数
2.树的度:树的所有结点中最大的度数
3.叶结点(Leaf):度为0的结点
4.父结点(Parent):有子树的结点是其子树的根结点的父结点
5.子结点(Child):若A结点是B结点的父结点,则称B结点是A结点的子结点;子结点也称孩子结点。
6.兄弟结点(Sibling):具有同一父结点的各结点彼此是兄弟结点。
7.路径和路径长度:从结点\(n_1\)到\(n_k\)的路径为一个结点序列\(n_1\) , \(n_2\),… , \(n_k\), \(n_i\)是 \(n_{i+1}\)的父结点。路径所包含边的个数为路径的长度。
9.祖先结点(Ancestor):沿树根到某一结点路径上的所有结点都是这个结点的祖先结点。
10.子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙。
11.结点的层次(Level):规定根结点在1层,其它任一结点的层数是其父结点的层数加1。
12.树的深度(Depth):树中所有结点中的最大层次是这棵树的深度。
二叉树(一种特殊的树)
对于一个二叉树,他的任何节点最多有两个子树,分别为左子树和右子树,二叉树的分支具有左右次序,不能随意颠倒。
三种特殊的二叉树
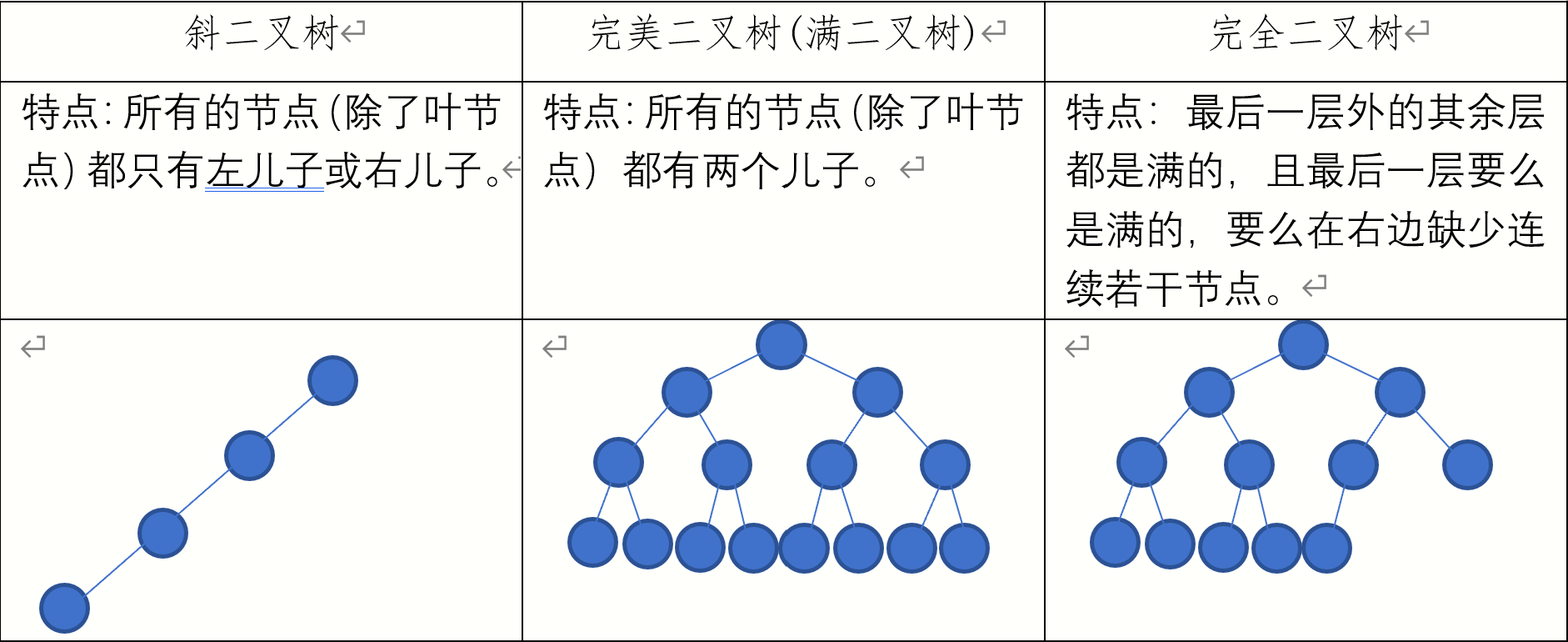
二叉树的性质
1.第i层最多有\(2^{i-1}\)个节点
2.深度为k的树最多有\(2_k-1\)个节点
3.对于一个非空二叉树用\(n\)k(k \(\in\) 0,1,2)表示有几个儿子的节点。有等式\(n_0\) = \(n_2\) + 1 恒成立。
证:
- 树的总边数 = \(n_0\) + \(n_1\) + \(n_2\) - 1(除了根节点外每个节点都有父节点)
- 树的总边数 = 0 * \(n_0\) + 1 * \(n_1\) + 2 * \(n_2\)(节点的下标代表了他有几个儿子也就是几条边)
- 联立可得\(n_0\) = \(n_2\) + 1
二叉树的实现
如果采用线性的储存方法,保存在数组中,根据上面的二分查找我们可以知道,二分查找顺序固定,可以行的通,但对于不是完美二叉树,会在空间上造成浪费,并不推荐。
常用的做法是采用链式储存下面给出树节点代码实现
struct TreeNode
{
ElementType Data;
BinTree Left;//指向左子树
BinTree Right;//指向右子树
};
二叉树的遍历
对于一颗二叉树,我们经常希望访问树中的每一个结点并且查看它的值。有很多常见的顺序来访问所有的结点,而且每一种都有有用的性质。
这里实现基于深度优先的前序中序后序遍历
对一棵树前序遍历,就是先访问它的根节点,再访问他的左子树,再访问他的右子树。
对一棵树中序遍历,就是先访问他的左子树,再访问它的根节点,再访问他的右子树。
对一棵树后序遍历,就是先访问他的左子树,再访问他的右子树,再访问它的根节点。
不难看出这三种遍历方式都可以用递归来实现,下面给出代码实现
#include<stdio.h>
#include<stdlib.h>
typedef struct TreeNode* BinTree;
#define ElementType int
struct TreeNode
{
ElementType Data;
BinTree Left;
BinTree Right;
};
//先序遍历
void PreOrderTraversal(BinTree T) {
//如果是空树就不遍历
if (T) {
printf("%d ", T->Data);
PreOrderTraversal(T->Left);
PreOrderTraversal(T->Right);
}
}
//中序遍历
void InOrderTraversal(BinTree T) {
//如果是空树就不遍历
if (T) {
InOrderTraversal(T->Left);
printf("%d ", T->Data);
InOrderTraversal(T->Right);
}
}
//后序遍历
void PostOrderTraversal(BinTree T) {
//如果是空树就不遍历
if (T) {
PostOrderTraversal(T->Left);
PostOrderTraversal(T->Right);
printf("%d ", T->Data);
}
}
通常情况下,用递归实现的方法都可以用循环来实现,对于三种遍历方法也是,仔细观察树遍历的路线图,不难发现,所走的路线是一样的,只是抛出的时机不同,前序遇到就抛出,中序遇到第2次抛出,后序是第三次抛出,根据这种特性我们可以通过堆栈来实现。
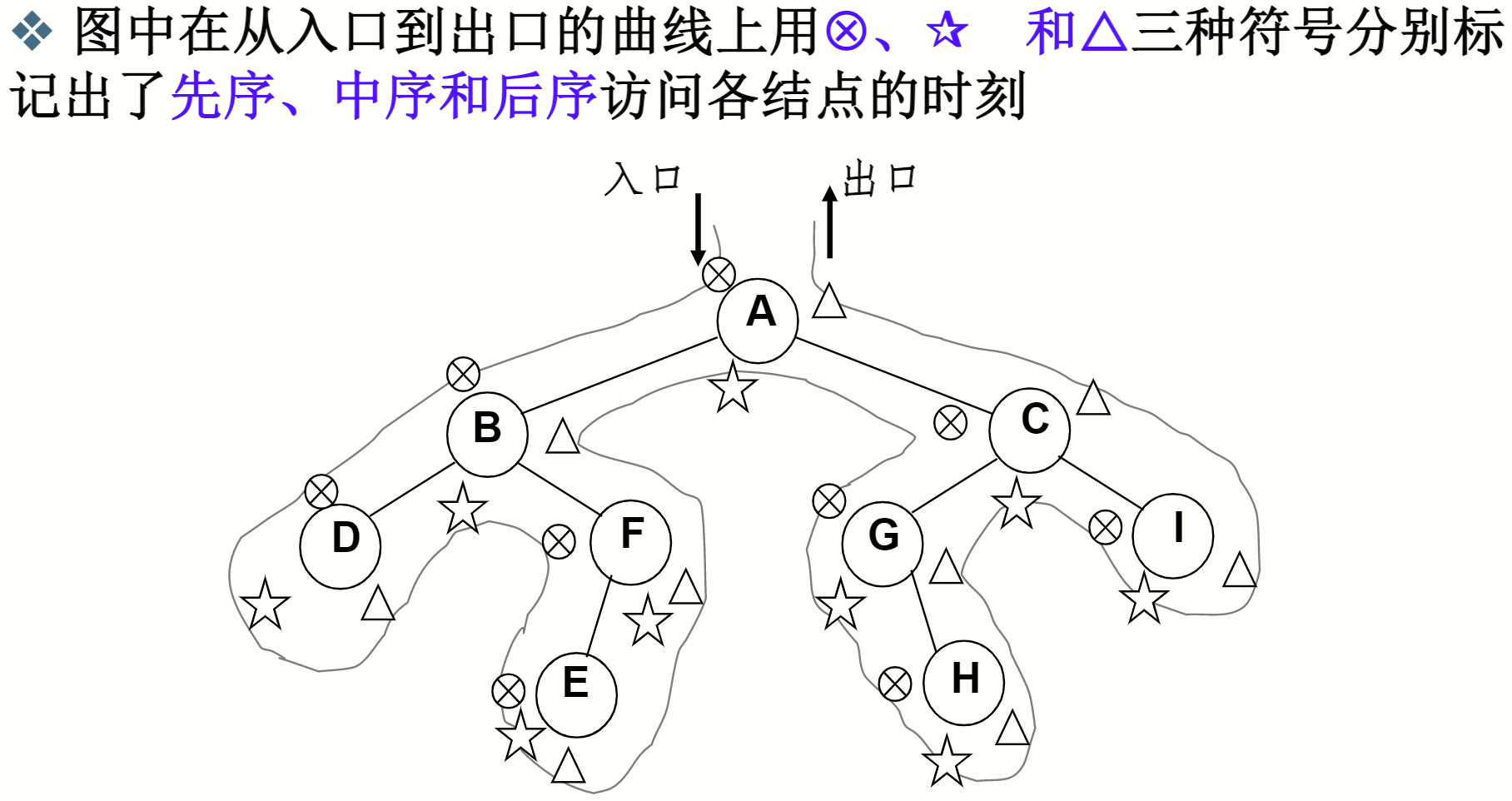
https://www.icourse163.org/course/ZJU-93001
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef struct SNode* Stack;
typedef struct TreeNode* BinTree;
#define ElementType1 int
#define ElementType2 BinTree
struct TreeNode
{
ElementType1 Data;
BinTree Left;
BinTree Right;
};
struct SNode
{
ElementType2 Data;
Stack Next;
};
//get link stack length,the empty stack has a header, the default length is 0
int length(Stack ptrs) {
Stack temp = ptrs;
int len = 0;
while (temp->Next) {
temp = temp->Next;
len++;
}
return len;
}
//make an empty linked Stack,generate an empty header(length is 1)
Stack makeEmpty() {
Stack ptrs;
ptrs = (Stack)malloc(sizeof(struct SNode));
ptrs->Next = NULL;
return ptrs;
}
//check the linklist is empty
bool isEmpty(Stack ptrs) {
if (length(ptrs) == 0) {
return true;
}
else {
return false;
}
}
//push
Stack push(ElementType2 value, Stack ptrs) {
Stack newLNode = (Stack)malloc(sizeof(struct SNode));
newLNode->Data = value;
newLNode->Next = ptrs->Next;
ptrs->Next = newLNode;
return ptrs;
}
//pop
ElementType2 pop(Stack ptrs) {
if (isEmpty(ptrs)) {
printf("the Stack has been empty.");
return NULL;
}
Stack temp = ptrs->Next;
ElementType2 value = temp->Data;
ptrs->Next = temp->Next;
free(temp);
return value;
}
//先序遍历
void PreOrderTraversal(BinTree T) {
Stack S = makeEmpty();
BinTree BT = T;
while (BT || !isEmpty(S)) {
while (BT) {
printf("%d ", BT->Data);
S = push(BT, S);
BT = BT->Left;
}
if (!isEmpty(S)) {
BT = pop(S);
BT = BT->Right;
}
}
}
//中序遍历
void InOrderTraversal(BinTree T) {
Stack S = makeEmpty();
BinTree BT = T;
while (BT || !isEmpty(S)) {
while (BT) {
S = push(BT, S);
BT = BT->Left;
}
if (!isEmpty(S)) {
BT = pop(S);
printf("%d ", BT->Data);
BT = BT->Right;
}
}
}
//后序遍历
void PostOrderTraversal(BinTree T) {
Stack S = makeEmpty();
BinTree BT = T;
while (BT || !isEmpty(S)) {
while (BT) {
S = push(BT, S);
BT = BT->Left;
}
if (!isEmpty(S)) {
BT = pop(S);
if (BT->Right) {
S = push(BT, S);
}
else {
printf("%d ", BT->Data);
}
BT = BT->Right;
}
}
}
除了深度优先遍历外还有广度优先遍历,和深度优先遍历不同,广度优先遍历会先访问离根节点最近的节点。二叉树的广度优先遍历又称按层次遍历。算法借助队列实现。
基本思路为,先把一个节点入队,再让一个节点出队,然后将该点的左右子树入队,先从根节点开始,一直到队列空就遍历完成整个树。
代码实现:
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef struct QNode* Queue;
typedef struct TreeNode* BinTree;
#define ElementType1 int
#define ElementType2 BinTree
struct TreeNode
{
ElementType1 Data;
BinTree Left;
BinTree Right;
};
struct QNode
{
ElementType2 Data;
Queue Next;
};
Queue makeEmpty() {
Queue Q = (Queue)malloc(sizeof(struct QNode));
Q->Next = NULL;
return Q;
}
void QueueAdd(ElementType2 value, Queue Q) {
Queue temp = Q->Next;
Queue newNode = (Queue)malloc(sizeof(struct QNode));
newNode->Data = value;
newNode->Next = temp;
Q->Next = newNode;
}
bool isEmpty(Queue Q) {
if (Q->Next == NULL) {
return true;
}
return false;
}
ElementType2 QueueDelete(Queue Q) {
Queue ptrq = Q;
if (!ptrq->Next) {
printf("The queue has been empty.");
return NULL;
}
while (ptrq->Next->Next) {
ptrq = ptrq->Next;
}
Queue temp = ptrq->Next;
ptrq->Next = NULL;
ElementType2 value = temp->Data;
free(temp);
return value;
}
//层序遍历
void LevelOrderTraversal(BinTree T) {
//空树直接退出
if (!T) {
return;
}
Queue Q = makeEmpty();
QueueAdd(T, Q);//先把根节点压入队列
while (!isEmpty(Q)) {
BinTree BT = QueueDelete(Q);//出队
printf("%d ", BT->Data);
//如果该节点左右还有节点就压入队列
if (BT->Left) {
QueueAdd(BT->Left, Q);
}
if (BT->Right) {
QueueAdd(BT->Right, Q);
}
}
课后练习题(3个小题)
03-树1 树的同构 (25point(s))
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。

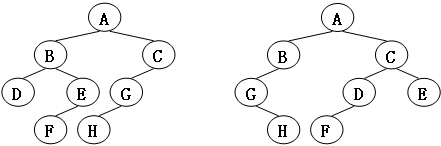
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No
代码实现:
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#define ElemrnntType char
#define MAXSIZE 10
#define Null -1
struct TreeNode
{
ElemrnntType Data;
int Left;
int Right;
}T1[MAXSIZE],T2[MAXSIZE];
int buildTree(struct TreeNode T[]) {
int N = 0;
int root = -1;
//注意看重点,一定要在这里读取加\n,要不会自闭的
scanf("%d\n", &N);
//用来检查哪个元素是根,默认都是0,在读入节点时,有指向的位置就不是
int check[MAXSIZE] = {0};
for (int i = 0; i < N;i++) {
char left, right ,data;
scanf("%c %c %c\n", &data, &left, &right);
T[i].Data = data;
T[i].Left = (left == '-') ? Null : (check[left - '0'] = 1, left - '0');
T[i].Right = (right == '-') ? Null : (check[right - '0'] = 1, right - '0');
}
for (int i = 0; i < N;i++) {
if (check[i] == 0) {
root = i;
break;
}
}
//返回根节点
return root;
}
//采用递归算法,每次传入一个树的子树作为新树
bool IsomorphicTree(int root1,int root2) {
//如果都是空的返回true
if (root1==Null&&root2==Null) {
return true;
}
//如果只有一颗空树返回false
if ((root1 == Null && root2 != Null)||(root1 != Null && root2 == Null)) {
return false;
}
//如果根节点不同返回false, 相同则进行下一次递归判别
if (T1[root1].Data != T2[root2].Data){
return false;
}
else {
//判断左右交换和没换只要有一种成立就返回true
return (IsomorphicTree(T1[root1].Left, T2[root2].Left) && IsomorphicTree(T1[root1].Right, T2[root2].Right)) ||
(IsomorphicTree(T1[root1].Left, T2[root2].Right) && IsomorphicTree(T1[root1].Right, T2[root2].Left));
}
}
int main() {
//读取2颗树
int root1 = buildTree(T1);
int root2 = buildTree(T2);
//判别是否为异构树
if (IsomorphicTree(root1, root2)) {
printf("Yes\n");
}
else {
printf("No\n");
}
}
03-树2 List Leaves (25point(s))
Given a tree, you are supposed to list all the leaves in the order of top down, and left to right.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤10) which is the total number of nodes in the tree -- and hence the nodes are numbered from 0 to N−1. Then N lines follow, each corresponds to a node, and gives the indices of the left and right children of the node. If the child does not exist, a "-" will be put at the position. Any pair of children are separated by a space.
Output Specification:
For each test case, print in one line all the leaves' indices in the order of top down, and left to right. There must be exactly one space between any adjacent numbers, and no extra space at the end of the line.
Sample Input:
8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6
Sample Output:
4 1 5
题目的意思就是传入一个树,要对该树层序遍历的顺序,打印出他的所有叶节点,与上一题一样,注意找出根节点。
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef struct QNode* Queue;
#define MAXSIZE 10
#define Null -1
struct TreeNode
{
int Left;
int Right;
}T[MAXSIZE];
struct QNode
{
int index;
Queue Next;
};
Queue makeEmpty() {
Queue Q = (Queue)malloc(sizeof(struct QNode));
Q->Next = NULL;
return Q;
}
void QueueAdd(int value, Queue Q) {
Queue temp = Q->Next;
Queue newNode = (Queue)malloc(sizeof(struct QNode));
newNode->index = value;
newNode->Next = temp;
Q->Next = newNode;
}
bool isEmpty(Queue Q) {
if (Q->Next == NULL) {
return true;
}
return false;
}
int QueueDelete(Queue Q) {
Queue ptrq = Q;
if (!ptrq->Next) {
printf("The queue has been empty.");
return -1;
}
while (ptrq->Next->Next) {
ptrq = ptrq->Next;
}
Queue temp = ptrq->Next;
ptrq->Next = NULL;
int value = temp->index;
free(temp);
return value;
}
int buildTree(struct TreeNode T[]) {
int N = 0;
int root = -1;
//注意看重点,一定要在这里读取加\n,要不会自闭的
scanf("%d\n", &N);
//用来检查哪个元素是根,默认都是0,在读入节点时,有指向的位置就不是
int check[MAXSIZE] = { 0 };
for (int i = 0; i < N; i++) {
char left, right, data;
scanf("%c %c\n", &left, &right);
T[i].Left = (left == '-') ? Null : (check[left - '0'] = 1, left - '0');
T[i].Right = (right == '-') ? Null : (check[right - '0'] = 1, right - '0');
}
for (int i = 0; i < N; i++) {
if (check[i] == 0) {
root = i;
break;
}
}
//返回根节点
return root;
}
//层序遍历出叶节点
void LevelOrderTraversal(int root) {
//空树直接退出
if (root==-1) {
return;
}
bool isfrist = true;
Queue Q = makeEmpty();
QueueAdd(root, Q);//先把根节点压入队列
while (!isEmpty(Q)) {
root = QueueDelete(Q);//出队
//叶节点就抛出
if ((T[root].Left == -1)&& (T[root].Right == -1)) {
if (isfrist) {
printf("%d", root);
isfrist = false;
}
else {
printf(" %d", root);
}
}
//如果该节点左右还有节点就压入队列
if (T[root].Left !=-1) {
QueueAdd(T[root].Left, Q);
}
if (T[root].Right !=-1) {
QueueAdd(T[root].Right, Q);
}
}
}
int main() {
//读取树
int root = buildTree(T);
//层序遍历叶节点
LevelOrderTraversal(root);
}
03-树3 Tree Traversals Again (25point(s))
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.
Output Specification:
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input:
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop
Sample Output:
3 4 2 6 5 1
题目的大意根据堆栈的顺序得到树,得到他的后序遍历,仔细观察不难发现,push的顺序对应了前序遍历,pop的顺序对应了中序遍历,所以对于该题的解法为,先将前序遍历顺序和中序遍历顺序保存在数组中,再根据前序遍历和中序遍历推导出后序遍历。因为后序遍历为左右根,所以可以采用堆栈的方法的,先将树的根堆入,再堆入右子树,再堆入左子树,递归完成。
代码实现:
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#define MAXSIZE 30
#define ElementType char
typedef struct SNode* Stack;
#define ElementType char
struct SNode
{
ElementType Data;
Stack Next;
};
char PreOrderTraversal[MAXSIZE];
char InOrderTraversal[MAXSIZE];
//get link stack length,the empty stack has a header, the default length is 0
int length(Stack ptrs) {
Stack temp = ptrs;
int len = 0;
while (temp->Next) {
temp = temp->Next;
len++;
}
return len;
}
//make an empty linked Stack,generate an empty header(length is 1)
Stack makeEmpty() {
Stack ptrs;
ptrs = (Stack)malloc(sizeof(struct SNode));
ptrs->Next = NULL;
return ptrs;
}
//check the linklist is empty
bool isEmpty(Stack ptrs) {
if (length(ptrs) == 0) {
return true;
}
else {
return false;
}
}
//push
Stack push(ElementType value, Stack ptrs) {
Stack newLNode = (Stack)malloc(sizeof(struct SNode));
newLNode->Data = value;
newLNode->Next = ptrs->Next;
ptrs->Next = newLNode;
return ptrs;
}
//pop
ElementType pop(Stack ptrs) {
if (isEmpty(ptrs)) {
printf("the Stack has been empty.");
return -1;
}
Stack temp = ptrs->Next;
ElementType value = temp->Data;
ptrs->Next = temp->Next;
free(temp);
return value;
}
//读入并返回读取几个节点
int read() {
int N = 0;
scanf("%d\n", &N);
Stack S = makeEmpty();
//
int preindex = 0;
int inindex = 0;
for (int i = 0; i < 2 * N; i++) {
char operation[10];
gets(operation);
//如果读取的操作(第二个字母是o),说明是pop,否则为push
if (operation[1]=='o') {
InOrderTraversal[inindex++] = pop(S);
}
else {
int end = 0;
while (operation[end] != '\0')end++;
char dest[3] = {""};
strncpy(dest, operation + 5, end-4);
dest[2] = '\0';
int num = atoi(dest);
PreOrderTraversal[preindex++] = num;
push(num, S);
}
}
return N;
}
//left 和 right 分别为传入树的在中序遍历的左右下标,root为当前树的根
void getpost(Stack S,int left,int right,int root) {
if (left > right) {
return;
}
else {
int index = left;
while (index < right && InOrderTraversal[index] != PreOrderTraversal[root]) {
index++;
}
push(PreOrderTraversal[root], S);
getpost(S,index+1,right,root+1+index-left);
getpost(S,left,index-1,root+1);
}
}
int main() {
/*
* 分析题目可以看出,push的顺序对应了先序遍历,push和pop出的序列是中序
* 所以题目无需建立树,只需要通过先序和中序还原后序遍历
*/
//读取先序序列和中序序列
int num = read();
//根据先序序列和中序序列生成后序遍历
Stack PostOrderTraversal = makeEmpty();
getpost(PostOrderTraversal, 0, num-1, 0);
//打印后序遍历
bool isfirst = true;
while (!isEmpty(PostOrderTraversal)) {
if (isfirst) {
printf("%d", pop(PostOrderTraversal));
isfirst = false;
}
else {
printf(" %d", pop(PostOrderTraversal));
}
}
}


