Google Kick Start 2020 Round D
Record Breaker
题意
给一个长为n的数组a,从左往右计算,如果某个a[i]比之前出现过的所有a[j]都更大,并且比a[i+1]更大,那么认为a[i]打破纪录,求有多少打破纪录的a[i]。
思路
遍历
代码
#include<bits/stdc++.h>
using namespace std;
const int MAX=2e5+5;
int a[MAX];
int main()
{
int T,cas=0;
scanf("%d",&T);
while(T--)
{
int n,maxx=-1,res=0;
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
a[n]=-1;
for(int i=0;i<n;i++)
{
if(a[i]>maxx&&a[i]>a[i+1])res++;
maxx=max(maxx,a[i]);
}
printf("Case #%d: %d\n",++cas,res);
}
}
Alien Piano
题意
给一个数组a,从左到右按照规则转化成数组b,b只有四种取值ABCD,规则如下:
- a[0]可以任意转化为ABCD
- 如果a[i]>a[i-1],那么要求b[i]>b[i-1]
- 如果a[i]<a[i-1],那么要求b[i]<b[i-1]
- 如果a[i]==a[i-1],那么要求b[i]==b[i-1]
- 如果对于某一位i,不能满足要求,那么视为一次违规,可以任意设置b[i]。
给定a,求最少有多少次违规。
思路
考虑遍历的同时维护当前位的可取的上下限,如果a[i]>a[i-1],那么要求b[i]>b[i-1],那么b[i]的下限一定要大于b[i-1],上限则不需要关注,因为可以不取到上限,并且只要求要求b[i]>b[i-1],那么b[i]直接可以取D,即上限为D。
同理,如果a[i]<a[i-1],那么要求b[i]<b[i-1],那么b[i]的上限一定要小于b[i-1]的上限,下限直接可以取到A。
只需要遍历过程中维护上下限,然后计算是否有下限超过D,或者上限小于A,如果有则当前位上下限重置,违规次数++。
代码
#include<bits/stdc++.h>
using namespace std;
const int MAX=1e4+5;
int a[MAX];
int main()
{
int T,cas=0;
scanf("%d",&T);
while(T--)
{
int n,res=0;
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
int ub=4,lb=1;
for(int i=1;i<n;i++)
{
if(a[i]>a[i-1])
lb++,ub=4;
if(a[i]<a[i-1])
ub--,lb=1;
if(lb>4||ub<1)
{
lb=1;
ub=4;
res++;
}
}
printf("Case #%d: %d\n",++cas,res);
}
}
Beauty of tree
题意
给一棵有n个节点的树,两个数A,B。然后分别独立的均匀分布的从1-n中选两个节点x,y,然后分别从x,y开始,每A,B个点涂色一次,如果有节点被重复涂色也只算一次。最后分数为数中被涂色的节点个数,求分数的期望。
思路
可以很简单的想到朴素的做法,把分数视为关于随机变量X,Y的函数F(X,Y),X,Y相互独立,二者的分布也已知,所以可以直接计算概率。
而F(X,Y),可以用一遍DFS求出选择每个节点对答案的贡献。期望就可以这样计算:
但是这样复杂度是O(n^2),不可接受。于是改变思路,对于任意一个节点v,将它的贡献视为1,然后求它被涂色的概率。由加法公式,有:
而对于P(X colored v)以及P(Y colored v),可以计算有多少节点被选择后按规则会对v进行涂色,记va[v]表示有va[v]个节点,被选择后每A个数涂色,会对v进行涂色,vb[v]同理。
不难得出
va,vb可以用一次DFS求出
DFS过程后根访问节点,记录到达当前节点v的路径,然后将va[v]++,然后寻找路径中往前A个节点u,然后va[u]+=va[v]。
vb同理。这样就可以计算每个节点的概率,时间复杂度为O(n)。
代码
#include<bits/stdc++.h>
using namespace std;
const int MAX=5e5+5;
vector<int> Tree[MAX];
double va[MAX],vb[MAX];
int path[MAX];
int n,a,b;
void dfs(int x,int d)
{
path[d-1]=x;
va[x]++;
vb[x]++;
for(int i=0;i<Tree[x].size();i++)
dfs(Tree[x][i],d+1);
if(d>a)
va[path[d-a-1]]+=va[x];
if(d>b)
vb[path[d-b-1]]+=vb[x];
}
int main()
{
int T,cas=0;
scanf("%d",&T);
while(T--)
{
scanf("%d%d%d",&n,&a,&b);
for(int i=1;i<=n;i++)
Tree[i].clear(),va[i]=0,vb[i]=0;
int x;
double res=0,nn=n;
for(int i=2;i<=n;i++)
scanf("%d",&x),Tree[x].push_back(i);
dfs(1,1);
for(int i=1;i<=n;i++)
{
res+=va[i]/nn+vb[i]/nn;
res-=va[i]*vb[i]/(nn*nn);
}
printf("Case #%d: %f\n",++cas,res);
}
}
Locked Doors
题意
给定n个房间,从左到右编号为 1~n ,每两个相邻房间中间有一道加密门,编号为 1~(n-1)。破解第i号门需要a[i]的代价,并且a[i]各不相同。假设从x号房间开始,每次选择左右两边代价较小的门打开,然后进入相邻的房间,直到走完所有房间,已经打开的门不会被关上。
现在有q个询问,对于每个询问给出开始的房间x,求第k个访问的房间号。
思路
挺难想的。看了官方题解发现是笛卡尔树。
对于任意一个门i,可以用栈找到其左侧第一个大于a[i]的门j,右侧第一个大于a[i]的门k,然后选择a[j],a[k]更小的那一个,假设为j,然后将i作为j的右儿子(同理如果是k则将i作为k的左儿子)建一棵二叉树。这样得到一棵第一关键字为下标i,第二关键字为a[i]的笛卡尔树。下标满足二叉排序树的特性,而a[i]满足大根堆的特性。以样例第二个数据为例。其建立出的笛卡尔树如下:
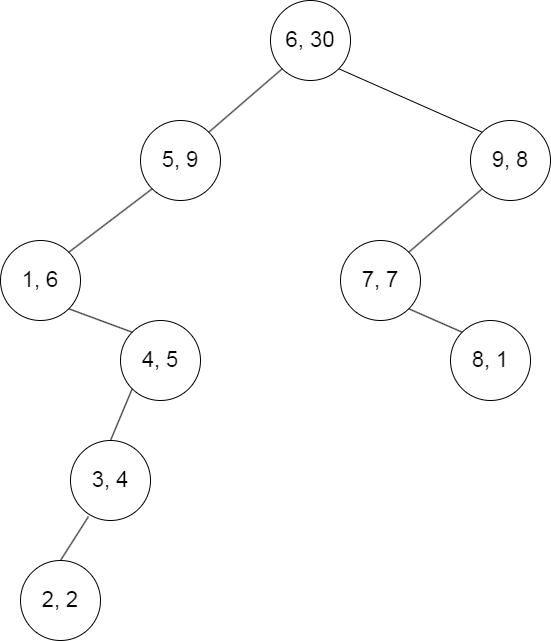
每个节点内部为(i,a[i]),并且每一棵子树的i连成一个连续区间。
从x号房间开始,记第一次打开的门编号为fd,然后从fd开始,每打开一扇门就对应进入一个房间。那么打开房间的过程可以看作遍历这棵树的过程。可以想到,从某一个节点开始,如果它有左子树,那么一定可以按从右往左的顺序访问子树中每个节点,因为子树中节点的代价一定小于当前节点,如果有右子树同理。并且可以想到,只有代价最大的门可能同时有左右子树,而第一次不可能开代价最大的门,所以初始节点一定只有最多一个儿子,或左或右。
假设从fd开始,如果以fd为根的子树大小大于k-1(因为第一个访问的房间已经确定,第二个开始每一道门对应一个房间),那么答案一定在fd为根的子树当中,如果有左子树,那么就从右往左访问k-1个就行了。右子树同理。
如果fd为根的子树大小小于k-1,那么可以向上找到第一个子树大小大于等于k-1的祖先v。
如果fd在v的左子树中,那么按照规则,应当先按顺序访问完fd子树中的节点,然后访问fd父亲,一直到v,然后如果还没到第k个,那么再按从左到右顺序访问v右子树。那么答案就是v+k-1-v左子树的大小
同理,如果fd在v右子树中,应当先按顺序访问完fd子树中的节点,然后访问fd父亲,一直到v,然后如果还没到第k个,那么再按从右到左顺序访问v左子树。那么答案就是v-k-v右子树的大小
建树用栈,时间复杂度O(n),寻找祖先用树上倍增O(logn),树上数据预处理用一次DFS,复杂度O(n),总体复杂度O(q*logn)
代码
#include<bits/stdc++.h>
using namespace std;
const int MAX=1e5+5;
const int LOGN=20;
struct Node
{
int siz,ls,rs;
}tree[MAX];
int d[MAX],nl_l[MAX],nl_r[MAX],fa[MAX][30],res[MAX];
void getnl(int n)
{
stack<int>st;
st.push(1);
for(int i=2;i<n;i++)
{
while(!st.empty()&&d[i]>d[st.top()])st.pop();
if(!st.empty())nl_l[i]=st.top();
st.push(i);
}
while(!st.empty())st.pop();
st.push(n-1);
for(int i=n-2;i>=1;i--)
{
while(!st.empty()&&d[i]>d[st.top()])st.pop();
if(!st.empty())nl_r[i]=st.top();
st.push(i);
}
}
int build(int n)
{
int rt;
d[0]=1e9+7;
for(int i=1;i<n;i++)
{
int ll=nl_l[i],rr=nl_r[i];
if(ll==rr&&ll==0)rt=i;
if(d[ll]<d[rr])
tree[ll].rs=i;
if(d[rr]<d[ll])
tree[rr].ls=i;
}
return rt;
}
void dfs(int x)
{
tree[x].siz=1;
for(int i=1; i<=LOGN; i++)
if(fa[x][i-1])
fa[x][i]=fa[fa[x][i-1]][i-1];
else break;
if(tree[x].ls!=-1)
{
int ls=tree[x].ls;
fa[ls][0]=x;
dfs(ls);
tree[x].siz+=tree[ls].siz;
}
if(tree[x].rs!=-1)
{
int rs=tree[x].rs;
fa[rs][0]=x;
dfs(rs);
tree[x].siz+=tree[rs].siz;
}
}
int main()
{
int T,cas=0;
scanf("%d",&T);
while(T--)
{
int n,q;
scanf("%d%d",&n,&q);
for(int i=1;i<n;i++)
{
nl_l[i]=nl_r[i]=0;
tree[i].siz=0;
tree[i].ls=tree[i].rs=-1;
scanf("%d",&d[i]);
for(int j=0;j<LOGN;j++)
fa[i][j]=0;
}
getnl(n);
int rt=build(n);
dfs(rt);
for(int qq=0;qq<q;qq++)
{
int x,k;
scanf("%d%d",&x,&k);
int fd;
if(x==1)fd=1;
else if(x==n)fd=n-1;
else fd=d[x]<d[x-1]?x:x-1;
k--;
if(tree[fd].siz>=k)
{
if(fd==x)
res[qq]=x+k;
if(fd==x-1)
res[qq]=x-k;
}
else
{
int cur=fd;
for(int i=LOGN;i>=0;i--)
if(fa[cur][i]&&tree[fa[cur][i]].siz<=k)
cur=fa[cur][i];
if(tree[cur].siz<k)cur=fa[cur][0];
if(fd<cur)
res[qq]=cur+k-tree[tree[cur].ls].siz;
else
res[qq]=cur+1-k+tree[tree[cur].rs].siz;
}
}
printf("Case #%d:",++cas);
for(int i=0;i<q;i++)
printf("% d",res[i]);
printf("\n");
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号