Educational Codeforces Round 135
A
题意
一个袋子有n种颜色的球,每种若干个,每次操作可以取出两个不同颜色的球,问最后留下的球可能是什么颜色。
思路
很显然,最后留下的是数量最多的那种颜色。因为可以每次选数量第二多的颜色和其他任意一个颜色取出。直到只剩一种颜色,而此时剩下的那种颜色数量不可能大于原来数量最多的颜色,两两匹配最后一定留下数量最多的那种颜色。
代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int n,x,maxx=-1,idx;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&x);
if(x>maxx)
{
idx=i+1;
maxx=x;
}
}
printf("%d\n",idx);
}
}
B
题意
按要求构造一个长为n的排列。给一个变量x,初始为零,从左到右遍历这个排列。
- 对于某一个pi,若x < pi,则x += pi 。否则x置0。
要求构造一个排列,使得最后x的值最大。
思路
可以观察到,要使得x一直增长,那么这种排列一定有
那么最后一位对答案的贡献一定大于前面所有位,那么只需要最后一位选n,前一位选n-1。然后注意一下构造规则就好了。
代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int n;
scanf("%d",&n);
if(n&1)
{
printf("1 %d ",n-2);
for(int i=n-3;i>=2;i--)
printf("%d ",i);
printf("%d %d\n",n-1,n);
}
else
{
for(int i=n-2;i>=1;i--)
printf("%d ",i);
printf("%d %d\n",n-1,n);
}
}
}
C
题意
给两个数组a,b。一种操作,把某个数x变为x的数位长度,如1230变为4,431变为3。求最少的操作,使得a,b中所含元素相同(位置不一定相同)。
思路
对于a数组中某一个数x,如果b数组中有相等的数,那么可以直接匹配,如果没有,那么或者需要用操作改变x,或者需要由b中的某个数y经过操作后变为x。
显然操作只能减小x,那么如果有比x更大的数,x有可能不需要操作,若没有,那么x肯定需要操作。所以可以想到从大到小考虑,每次取a,b中各自最大数x,y。若x==y,那么可以直接匹配,不需要操作,如果存在x<y或者y>x,那么就对较大的数进行一次操作再重新选择两边最大的数。可以使用大顶堆很方便的实现。
代码
#include<bits/stdc++.h>
using namespace std;
const int MAX=2e5+5;
int a[MAX],b[MAX],cnt[15];
priority_queue<int> Qa,Qb;
int len(int x)
{
int res=0;
while(x)
{
res++;
x/=10;
}
return res;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int n,x,res=0;
memset(cnt,0,sizeof cnt);
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&a[i]),Qa.push(a[i]);
for(int i=0;i<n;i++)
scanf("%d",&b[i]),Qb.push(b[i]);
while(!Qa.empty())
{
if(Qa.top()==Qb.top())
{
Qa.pop();
Qb.pop();
continue;
}
res++;
if(Qa.top()>Qb.top())
{
Qa.push(len(Qa.top()));
Qa.pop();
}
else
{
Qb.push(len(Qb.top()));
Qb.pop();
}
}
printf("%d\n",res);
}
}
D
题意
给一个字符串S,长为偶数。AB二人博弈,轮流操作,每次可以取走S最前或最后的字符,插入各自的字符串中。最后自己的字符串字典序较小的人获胜。求最终谁获胜。
思路
博弈论,可以画一下博弈图。
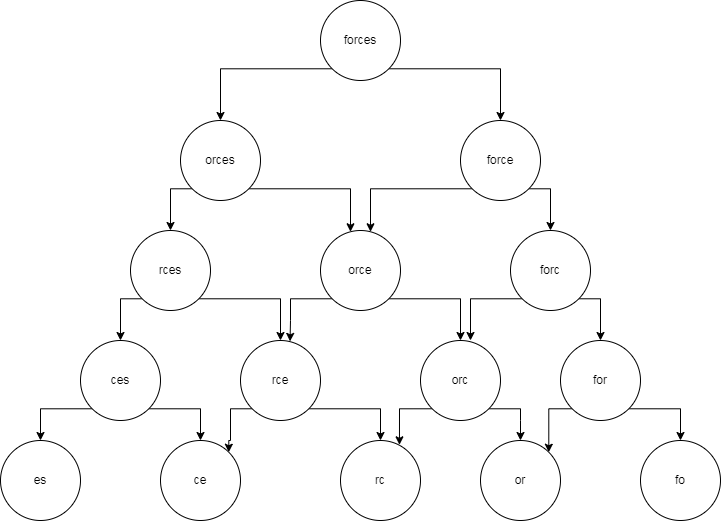
可以看到,这个游戏是先手必定不败的,因为每次先手都可以确定一个更优的值,并且当只剩两个元素时,先手的人总可以选择一个更优的值,所以一定先手必定不败。
对于某一个串abcd,一次轮流博弈可以转移到三个状态[ab]cd,[a]bc[d],ab[cd],[]表示被选择掉的字符。定义某一个状态dp["abcd"]为1表示此状态先手必胜,为0则表示先手必定平局。
因为最后比较字典序,所以博弈过程中的选择也会影响两人胜负,所以每次要考虑两人选择字符是否一直,所以每次转移考虑一次轮流博弈,按照博弈图进行状态转移。
如果A首先选了a,那么B可以选择b,d,如果A首先选择d,那么B可以选择a,c,对于转移得到的三个状态,如果无论A先选a还是d,B都能找到c或者b使得二人选择的字符相等,并且子状态也是0,那么当前为先手必平,否则为先手必胜。
最后用记忆化搜索实现一下比较好写。
代码
#include<bits/stdc++.h>
using namespace std;
const int MAX=2e3+3;
char s[MAX];
int dp[MAX][MAX];
bool dfs(int l,int r)
{
if(dp[l][r]!=-1)return dp[l][r];
if(r-l==1)return dp[l][r]=(s[l]!=s[r]);
bool LL=!dfs(l,r-2),MM=!dfs(l+1,r-1),RR=!dfs(l+2,r);
if(MM&&s[l]==s[r])return dp[l][r]=0;
if((LL&&s[r]==s[r-1])&&(RR&&s[l]==s[l+1]))return dp[l][r]=0;
return dp[l][r]=1;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
memset(dp,-1,sizeof dp);
scanf("%s",s);
int n=strlen(s);
if(dfs(0,n-1))
printf("Alice\n");
else
printf("Draw\n");
}
}
E
题意
有n个盘子,红色,黑色两种调料,每个盘子里面可以任选一种调料加入,提高ai,bi的美味度。求最高的美味度之和。除此之外,限制调料只能整包购买,一整包红色调料有x个红色调料,一整包黑色调料有y个黑色调料,有q个询问,每个询问给定xi,yi,分别表示一整包红色,一种包黑色包含的各自颜色调料的数量。对每个询问,输出在这种条件下的最高美味度。
思路
显然可以得到,每次询问对应一个方程(r表示购买r整包红色,b表示购买b整包黑色。)
然后很容易想到,最优解应该是ai>bi时选红色,ai<bi时选黑色,那么就要找到符合方程(1)限制的最接近最优解的答案就是最高美味度。
所以想到可以先全部选黑色,然后逐渐把红色贡献更大的盘子换成红色,不难想到这个替换过程是一个单峰函数。
同时,方程(1)的解可以有以下公式推导。
按照题意,只需要保留非负整数解,所以有
可以想到k在范围内变化的过程就是一个单峰函数,所以可以用三分法在O(logn)时间内处理得到一个查询的最优解。
代码实现用扩展欧几里得求方程的解,三分求最大值。
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAX=3e5+5;
ll d[MAX],pre[MAX];
int n,q,a,b;
ll x,y,g,sum=0;
ll exgcd(ll a,ll b,ll& x,ll& y)
{
if(!b)
{
x=1;
y=0;
return a;
}
ll d=exgcd(b,a%b,x,y);
ll t=x;
x=y;
y=t-(a/b)*y;
return d;
}
inline ll f(int k)
{
ll red=(n/g*x+b/g*k)*a;
ll cur=sum;
cur-=pre[red];
return cur;
}
ll sanfen_integer(int l,int r)
{
ll res=max(f(l),f(r));
while(l<r-1)
{
int mid=(l+r)>>1;
int mmid=(mid+r)>>1;
if(f(mid)>f(mmid))
res=max(res,f(mid)),r=mmid;
else
res=max(res,f(mmid)),l=mid;
}
res=max(res,max(f(l),f(r)));
return res;
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d%d",&a,&b);
d[i]=b-a;
sum+=b;
}
sort(d,d+n);
for(int i=0;i<n;i++)
pre[i+1]=pre[i]+d[i];
scanf("%d",&q);
while(q--)
{
scanf("%d%d",&a,&b);
g=exgcd(a,b,x,y);
if(n%g)
{
printf("-1\n");
continue;
}
ll l=ceil(double(n)/double(b)*(-x));
ll r=floor(double(n)/double(a)*y);
if(l>r)
{
printf("-1\n");
continue;
}
ll res=sanfen_integer(l,r);
printf("%I64d\n",res);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号