数据集成、变换、归约及相关MATLAB工具箱函数

　　数据预处理的主要内容包括数据清洗、数据集成、数据变换和数据规约，在数据挖掘的过程中，数据预处理工作量占到了整个过程的60%。数据清洗在上一篇博客中写过，这里主要写后面三部分。

数据集成

　　数据挖掘需要的数据往往分布在不同的数据源中，数据集成就是将多个数据源合并存放在一个一致的数据存储（如数据仓库）中的过程。

　　在数据集成时，来自多个数据源的现实世界实体的表达形式是不一样的，有可能不匹配，要考虑实体识别问题和属性冗余问题，从而将源数据在最低层上加以转换、提炼和集成。

　　1、实体识别

　　同名异义、异名同义、单位不统一

　　2、冗余项识别

　　数据集成往往导致数据冗余，如：

　　①同一属性多次出现。

　　②同一属性命名不一致导致重复。

　　有些冗余属性可以用相关分析检测。给定两个数值型的属性A和B，根据其属性值，用相关系数度量一个属性在多大程度上蕴含另一个属性。

数据变换

　　数据变换主要是对数据进行规范化处理，将数据转换成适当的形式，以适用于挖掘任务及算法的需要。

简单的函数变换

　　常见的函数变换有平方、开方、取对数、差分等。$$\begin{array}{*{20}{l}}
{{x^\prime } = {x^2}}\\
{{x^\prime } = \sqrt x }\\
{{x^\prime } = \log (x)}\\
{\nabla f\left( {{x_k}} \right) = f\left( {{x_{k + 1}}} \right) - f\left( {{x_k}} \right)}
\end{array}$$

　　简单的函数变换常用来将不具有正态分布的数据变换成具有正态分布的数据；在时间序列分析中，有时简单的对数变换或者差分运算就可以将非平稳序列转换成平稳序列。 

规范化

　　数据标准化（归一化）处理是数据挖掘的一项基础工作。不同评价指标往往具有不同的量纲，数值间的差别可能很大，不进行处理可能会影响到数据分析的结果。为了消除指标之间的量纲和取值范围差异的影响，需要进行规范化处理，将数据按照比例进行缩放，使之落入一个特定的区域，便于进行综合分析。

　　①最小-最大规范化

　　也称为离差标准化，是对原始数据的线性变换，将数值映射到[0，1]区间。

　　公式如下：$$x^{*}=\frac{x-\min }{\max -\min }$$

　　其中，max为样本数据的最大值，min为样本数据的最小值，max-min为极差。

　　离差标准化保留了原来数据中存在的关系，是消除量纲和数据取值范围影响的最简单的方法。

　　这种处理方法的缺点是若数值集中或某个数值很大，则规范化后各值会接近于0，并且将会相差不大。若将来遇到超过目前属性[min，max]取值范围的时候，会引起系统出错，需要重新确定min和max。

　　②零-均值规范化

　　也叫标准差标准化，经过处理的数据的均值为0，标准差为1。

　　公式如下：$$x^{*}=\frac{x-\overline{x}}{\sigma}$$

　　其中$\overline x $为原始数据的均值；$\sigma $为原始数据的标准差。这种方法是当前用得最多的数据标准化方法，但是均值和标准差受离群点的影响很大，因此通常需要修改上述变换。

　　首先，用中位数M取代均值，其次用绝对标准差取代标准差$\sigma^{*}=\sum_{i=1}^{i=n}\left|x_{i}-W\right|$，W是平均数或者中位数。

　　③小数定标规范化

　　通过移动属性值的小数位数，将属性值映射到[-1，1]之间，移动的小数位数取决于属性值绝对值的最大值。

　　公式如下：$$x^{*}=\frac{x}{10^{k}}$$

　　对于一个含有n个记录、p个属性的数据集，就分别对每一个属性的取值进行最小-最大规范化、零-均值规范化、小数定标规范化进行规范化。

%% 数据规范化
clear;
% 参数初始化：
data = '../data/normalization_data.xls';
%% 读取数据
[data,~] = xlsread(data);
%% 最小-最大规范化
data_scatter = mapminmax(data',0,1); % 数据需要转置
data_scatter = data_scatter';
%% 零-均值规范化
data_zscore = zscore(data);
%% 小数定标规范化
max_ = max(abs(data));
max_ = power(10,ceil(log10(max_)));
cols = size(max_,2);
data_dot = data;
for i=1:cols
    data_dot(:,i)=data(:,i)/max_(1,i);
end
%% 打印结果
disp('原始数据为：');
disp(data);
disp('最小-最大规范化后的数据为：');
disp(data_scatter);
disp('零-均值规范化后的数据为：');
disp(data_zscore);
disp('小数定标规范化后的数据为：');
disp(data_dot);

连续属性离散化

　　一些数据挖掘算法，特别是某些分类算法如ID3算法、Apriori算法等，要求数据是分类属性形式。这样，常常需要将连续属性变换成分类属性，即连续属性离散化。

　　1、离散化的过程

　　连续属性的离散化就是在数据的取值范围内设定若干个离散的划分点，将取值范围划分为一些离散化的区间，最后用不同的符号或整数值代表落在每个子区间中的数据值。

　　所以，离散化涉及两个子任务：确定分类数以及如何将连续属性值映射到这些分类值中。

　　2、常用的离散化方法

　　常用的离散化方法有等宽法、等频法和聚类分析法。

　　①等宽法

　　将属性的值域分成具有相同宽度的区间，区间的个数由数据本身的特点决定或者用户指定，类似于制作频率分布表。

　　②等频法

　　将相同数量的记录放进每个区间。

　　这两种方法简单、易于操作，但都需要人为地规定划分区间的个数。

　　缺点：

　　等宽法的缺点在于它对离群点比较敏感，倾向于不均匀地把属性值分布到各个区间。有些区间包含许多数据，而另外一些区间的数据极少，这样会严重损坏所建立的决策模型。

　　等频法虽然避免了上述问题的产生，却可能将相同的数据值分到不同的区间以满足每个区间中固定的数据个数。

　　③聚类分析

　　聚类分析法包括两个步骤，首先将连续属性的值用聚类算法进行聚类，然后再将聚类得到的簇进行处理，合并到一个簇的连续属性值做同一标记。

　　聚类分析的离散化方法也需要用户指定簇的个数，从而决定产生的区间数。

%% 数据离散化
clear;
% 参数初始化：
data = '../data/discretization_data.xls';
k = 4; 
%% 读取数据
[data,~] = xlsread(data);
rows = size(data,1);
%% 等宽离散化
% 规则需要自定义
rules = [0,0.179,0.258,0.35,0.504];
width_data = zeros(rows,2);
width_data(:,1) = data;
width_data(:,2)= arrayfun(@find_type,data);
%% 等频离散化
frequent_data = zeros(rows,2);
frequent_data(:,1) = data;
end_ =-1;
for i=1:k-1
    start_ = floor((i-1)*rows/k)+1;
    end_ = floor(i*rows/k);
    frequent_data(start_:end_,2) = i;
end
frequent_data(end_+1:end,2) = k;
%% 聚类离散化
[idx,~] = kmeans(data,k);
cluster_data = zeros(rows,2);
cluster_data(:,1) = data;
cluster_data(:,2) = idx;
%% 作图展示结果
figure
cust_subplot(width_data,3,1,1,k,'等宽离散化');
cust_subplot(frequent_data,3,1,2,k,'等频离散化');
cust_subplot(cluster_data,3,1,3,k,'聚类离散化');
disp('数据离散化完成！');

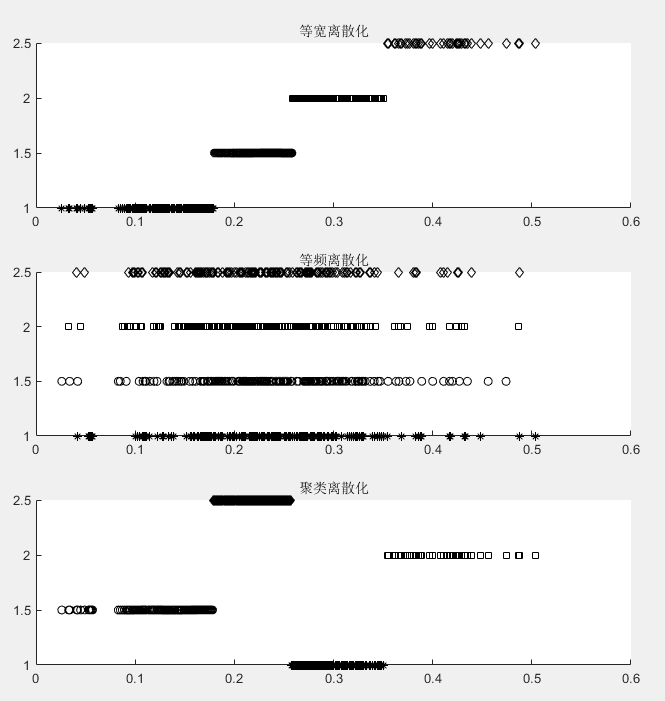
　　分别用等宽法、等频法和聚类分析法对数据进行离散化，将数据分成四类，然后将每一类记为同一个标识，再进行建模。

属性构造

　　在数据挖掘的过程中，为了帮助提取更有用的信息、挖掘更深层次的模式，提高挖掘结果的精度，需要利用已有的属性集构造出新的属性，并加到现有的属性集合中。

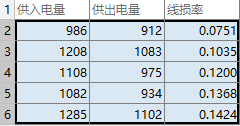
　　比如进行防窃漏电诊断建模时，已有的属性包括供入电量、供出电量（线路上各大用户用电量之和）。理论上供入电量和供出电量应该是相等的，但是由于在传输过程中存在电能损耗，使得供入电量略大于供出电量，如果该条线路上的一个或多个大用户存在窃漏电行为，会使得供入电量明显大于供出电量。反过来，为了判断是否有大用户存在窃漏电行为，可以构造出一个新的指标—线损率，该过程就是构造属性。

　　新构造的属性线损率按以下公式计算：

　　

　　线损率的正常范围一般在3%~15%，如果远远超过该范围，就可以认为该条线路的用户很可能存在窃漏电等用电异常的行为。

%% 线损率属性构造
clear;
%初始化参数
inputfile= '../data/electricity_data.xls';       % 供入供出电量数据
outputfile = '../tmp/electricity_data.xls';  % 属性构造后数据文件
%% 读取数据
[num,txt,raw]=xlsread(inputfile);                   % 数据第一列为供入电量，第二列为供出电量
[rows,cols] = size(num);
%% 构造属性
loss = (num(:,1)-num(:,2))./num(:,1);
%% 保存结果
result = cell(rows+1,cols+1);
result(:,1:cols) =raw;
result{1,cols+1} = '线损率';
result(2:end,cols+1) = num2cell(loss);
xlswrite(outputfile,result);
disp('线损率属性构造完毕！');

 

小波变换

　　傅里叶变换与小波变换强烈安利：http://cda.pinggu.org/view/18623.html，慢慢看。

　　基于小波变换的特征提取方法主要有：①基于小波变换的多尺度空间能量分布特征的提取、②基于小波变换的多尺度空间中模极大值特征的提取、③基于小波包变换特征的提取、④基于适应性小波神经网络特征的提取。

　　小波基函数：

　　小波基函数是一种具有局部支集的函数，并且平均值为0，小波基函数满足：$\psi(0)=\int \psi(t) \mathrm{d} t=0$。常用的小波基有Haar小波基、db系列小波基等。

　　小波变换：

　　对小波基函数进行伸缩和平移变换：$\psi_{a, b}(t)=\frac{1}{\sqrt{|a|}} \psi\left(\frac{t-b}{a}\right)$

　　其中，a为伸缩因子；b为平移因子。

　　任意函数$f(t)$的连续小波变换（CWT）为：$$W_{f}(a, b)=|a|^{-1 / 2} \int f(t) \psi\left(\frac{t-b}{a}\right) \mathrm{d} t$$

　　可知，连续小波变换为$f(t) \rightarrow W_{f}(a, b)$的映射，对小波基函数$\psi(t)$增加约束条件$C_{\psi}=\int \frac{|\hat{\psi}(t)|^{2}}{t} \mathrm{d} t<\infty$就可以由$W_{f}(a, b)$逆变换得到$f(t)$。其中$\hat{\psi}(t)$为$\psi(t)$的傅里叶变换。其逆变换为：$$f(t) = \frac{1}{{{C_\psi }}}{W_f}(a,b)\psi \left( {\frac{{t - b}}{a}} \right){\rm{d}}a \cdot {\rm{d}}b$$

 　　利用小波函数对声波信号数据进行分解，得到5个层次的小波系数。利用这些小波系数求得各个能量值，这些能量值即可作为声波信号的特征数据。

%% 利用小波分析 进行特征分析
clear;
% 参数初始化
level =5;
load leleccum;
signal = leleccum(1:3920);
%% 进行 level层小波分解
[C,S] = wavedec2(signal,level,'bior3.7');
%% 提取第i层小波系数,并计算各层能量值
E=zeros(1,level);
for i=1:level
    [H_i,~,~] = detcoef2('all',C,S,i);
    E(1,i)=norm(H_i,'fro');
end
%% 打印各层能量值，即提取的特征值
disp('声音信号小波分析完成，提取的特征向量为：');
disp(E);

得到声音信号的特征向量如下所示：

数据规约

　　在大数据集上进行复杂的数据分析和挖掘将需要很长的时间，数据规约产生更小的但保持原数据完整性的新数据集。在规约后的数据集上进行分析和挖掘将更有效率。

　　数据规约的意义在于：

　　①降低无效、错误数据对建模的影响，提高建模的准确性。口少量且具代表性的数据将大幅缩减数据挖掘所需的时间。

　　②降低储存数据的成本。

属性规约

　　属性规约通过属性合并创建新属性维数，或者直接通过删除不相关的属性维数来减少数据维数，从而提高数据挖掘的效率、降低计算成本。属性规约的目标是寻找出最小的属性子集并确保新数据子集的概率分布，并尽可能地接近原来数据集的概率分布。

　　属性规约常用方法：(限于篇幅，这里浅显的写一点点，其实这样效果并不好，建议看一些机器学习和数据挖掘的教材)

　　①合并属性

　　将一些旧属性合并为新属性。

　　②逐步向前选择

　　从一个空属性集开始；每次从原来属性集合中选择一个当前最优的属性添加到当前属性子集中。直到无法选择出最优属性或满足一定阀值约束为止。

　　③逐步向后删除

　　从一个全属性集开始，每次从当前属性子集中选择一个当前最差的属性并将其从当前属性子集中消去，直到无法选择出最差属性为止或满足一定阀值约束为止。

　　⑤决策树归纳

　　利用决策树的归纳方法对初始数据进行分类归纳学习，获得一个初始决策树，所有没有出现在这个决策树上的属性均可认为是无关属性，因此将这些属性从初始集合中删除，就可以获得一个较优的属性子集。

　　⑥主成分分析

　　用较少的变量去解释原始数据中的大部分变量，将许多相关性很高的变量转化成彼此相互独立或不相关的变量。

　　下面以主成分分析为例。

　　逐步向前选择、逐步向后删除和决策树归纳是属于直接删除不相关属性维数的方法。

　　而主成分分析是一种用于连续属性的数据降维方法，它构造了原始数据的一个正交变换，新空间的基底去除了原始空间基底数据的相关性，只需使用少数新变量就能够解释原始数据中的大部分变异。

　　在应用中，通常是选出比原始变量个数少，能解释大部分数据中的变量的几个新变量，即所谓的主成分，来代替原始变量进行建模。

 　　步骤：

　　①设原始变量$X_{1}, X_{2}, \cdots, X_{p}$的n次观测数据矩阵为：　　$$X=\left[\begin{array}{ccc}{x_{11}} & {x_{12}} & {\cdots} & {x_{1 p}} \\ {x_{21}} & {x_{22}} & {\cdots} & {x_{2 p}} \\ {\vdots} & {\vdots} & {} & {\vdots} \\ {x_{n 1}} & {x_{n 2}} & {\cdots} & {x_{n p}}\end{array}\right] A\left(X_{1}, X_{2}, \cdots, X_{P}\right)$$

　　②将数据矩阵按列进行中心标准化。为了方便，将标准化后的数据矩阵仍然记为X。

　　③求相关系数矩阵$R, R=\left(r_{i j}\right)_{p \cdot p}, \quad r_{i j}$定义为

$$r_{i j}=\sum_{k=1}^{n}\left(x_{k i}-\overline{x}_{i}\right)\left(x_{k j}-\overline{x}_{j}\right) / \sqrt{\sum_{k=1}^{n}\left(x_{k i}-\overline{x}_{i}\right)^{2} \sum_{k=1}^{n}\left(x_{k j}-\overline{x}_{j}\right)^{2}}$$

　　其中，$r_{j}=r_{j, i}, r_{i i}=1$

　　④求R的特征方程$\operatorname{det}(R-\lambda E)=0$的特征根$\lambda_{1} \geqslant \lambda_{2} \geqslant \cdots \geqslant \lambda_{p}>0$

　　⑤确定主成分个数m：$\frac{\sum_{i=1}^{m} \lambda_{i}}{\sum_{i=1}^{p} \lambda_{i}} \geqslant \alpha$。a根据实际问题确定，一般取80%。

　　⑥计算m个相应的单位特征向量：$$\beta_{1}=\left[\begin{array}{c}{\beta_{11}} \\ {\beta_{21}} \\ {\vdots} \\ {\beta_{p 1}}\end{array}\right], \beta_{2}=\left[\begin{array}{c}{\beta_{12}} \\ {\beta_{22}} \\ {\vdots} \\ {\beta_{p 2}}\end{array}\right], \ldots, \beta_{m}=\left[\begin{array}{c}{\beta_{m 2}} \\ {\beta_{x 2}} \\ {\vdots} \\ {\beta_{m 2}}\end{array}\right]$$

　　⑦计算主成分：$$Z_{i}=\beta_{1 i} X_{1}+\beta_{2 i} X_{2}+\dots+\beta_{p i} X_{p}(i=1,2, \cdots, m)$$

%% 主成分分析 降维
clear;
% 参数初始化
inputfile = '../data/principal_component.xls';
outputfile = '../tmp/dimention_reducted.xls'; % 降维后的数据
proportion = 0.95 ; % 主成分的比例
%% 数据读取
[num,~] = xlsread(inputfile);
%% 主成分分析
[coeff,~,latent] = pca(num);
%% 计算累计贡献率，确认维度
sum_latent = cumsum(latent/sum(latent)); % 累计贡献率
dimension = find(sum_latent>proportion);
dimension= dimension(1);
%% 降维
data = num * coeff(:,1:dimension); 
xlswrite(outputfile,data);
disp('主成分特征根：');
disp(latent');
disp('主成分单位特征向量');
disp(coeff);
disp('累计贡献率');
disp(sum_latent');
disp(['主成分分析完成，降维后的数据在' outputfile]);

 　　从结果可以得到特征方程有7个特征根、对应的7个单位特征向量以及累计贡献率。

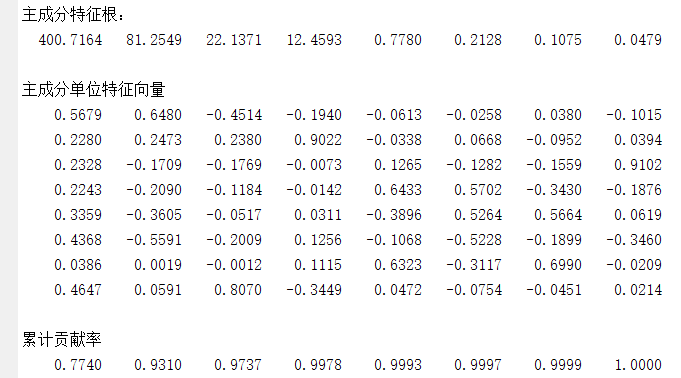
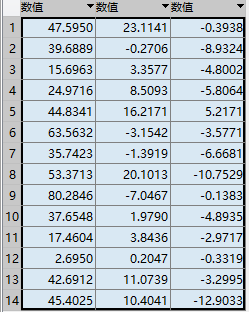
　　原始数据从8维被降维到了3维，同时这3维数据占了原始数据95%以上的信息。

数值规约

　　数值规约通过选择替代的、较小的数据来减少数据量，包括有参数方法和无参数方法两类。

　　有参数方法是使用一个模型来评估数据，只需存放参数，而不需要存放实际数据。例如，回归（线性回归和多元回归）和对数线性模型（近似离散属性集中的多维概率分布）。

　　无参数方法就需要存放实际数据，例如，直方图、聚类、抽样（采样）、参数回归。

　　1.直方图

　　直方图使用分箱来近似数据分布，是一种流行的数据规约形式。属性A的直方图将A的数据分布划分为不相交的子集或桶。如果每个桶只代表单个属性值/频率对，则该桶称为单桶。通常，桶表示给定属性的一个连续区间。

　　2.聚类

　　聚类技术是将数据元组（即记录，数据表中的一行）视为对象。它将对象划分为簇，使一个簇中的对象相互“相似”，而与其他簇中的对象“相异”。在数据规约中，用数据的簇替换实际数据。该技术的有效性依赖于簇的定义是否符合数据的分布性质。

　　3.抽样

　　抽样也是一种数据规约技术，它用比原始数据小得多的随机样本（子集）表示原始数据集。假定原始数据集D包含N个元组，可以采用抽样方法对D进行抽样。下面介绍常用的抽样方法。

　　①s个样本无放回简单随机抽样：从D的N个元组中抽取s个样本（s<N），其中D中任意元组被抽取的概率均为1/N，即所有元组的抽取是可能相等的。

　　②s个样本有放回简单随机抽样：该方法类似于无放回简单随机抽样，其不同在于每次一个元组从D中抽取后，记录它，然后放回原处。

　　③聚类抽样：如果D中的元组分组放人M个互不相交的“簇”，则可以得到s个簇的简单随机抽样，其中s<M。例如，数据库中元组通常一次检索一页，这样每页就可以视为一个簇。

　　④分层抽样：如果D划分成互不相交的部分，称做层，则通过对每一层的简单随机抽样就可以得到D的分层样本。

　　用于数据规约时，抽样最常用来估计聚集查询的结果。在指定的误差范围内，可以确定（使用中心极限定理）估计一个给定的函数所需的样本大小。通常样本的大小s相对于N非常小。而通过简单地增加样本大小，这样的集合可以进一步求精。

　　4.参数回归

　　简单线性模型和对数线性模型可以用来近似给定的数据。用简单线性模型对数据建模，使之拟合为一条直线。

　　把点对（2，5）、（3，7）、（4，9）、（5，12）、（6，11）、（7，15）、（8，18）、（9，19）、（11，22）、（12，25）、（13，24）、（15，30）、（17，35）规约成线性函数$y = wx + b$，即拟合函数 $y = 2x + 1.3$ 线上所对应的点可以近似地看做是已知点，如图4-9所示。

clc
clear
x=[2,3,4,5,6,7,8,9,11,12,13,15,17];
y=[5,7,9,12,11,15,18,19,22,25,24,30,35];
% 绘制散点图，判断是否具有线性关系
figure
plot(x,y,'r*')                         %作散点图
set(gca,'linewidth',2);
% 采用最小二乘拟合
Lxx=sum((x-mean(x)).^2); 
Lxy=sum((x-mean(x)).*(y-mean(y)));
b1=Lxy/Lxx;
b0=mean(y)-b1*mean(x);
y1=b1*x+b0;
hold on
plot(x, y1,'linewidth',2);

 

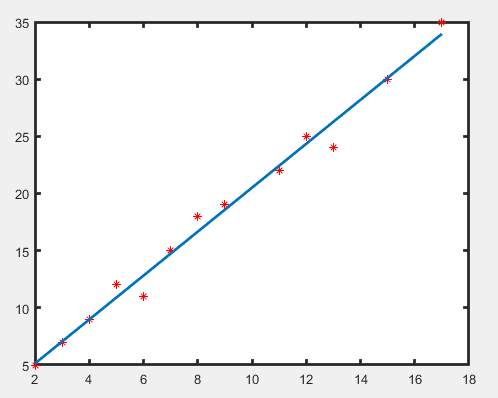
 　　其中，y的方差是常量13.44。在数据挖掘中，x和y是数值属性。系数2和1.3（称做回归系数）分别为直线的斜率和y轴截距。系数可以用最小二乘方法求解，它使数据的实际直线与估计直线之间的误差最小化。多元线性回归是（简单）线性回归的扩充，允许响应变量y建模为两个或多个预测变量的线性函数。

MATLAB主要的数据预处理函数

　　①interp1()

　　功能：一维数据插值。

　　使用格式：yi=interp1(x，Y，xi，method)，进行一维数据的线性插值。

　　参数X和Y表示已知数据，其中，X为向量，Y为与X同维向量或行数等于x长度的矩阵。xi为向量，表示待插入点，如果Y为向量，则xi中元素通过向量X与Y的内插值得到yi；如果Y为一矩阵，则xi中的元素通过对向量X与矩阵Y的每列分别进行内插值得到yi。

　　②unique()

　　功能：去除数据中的重复元素，得到单值元素列表。

　　使用格式：[b，i，jl=unique(x)，将数据矩阵X中的元素去重复后，返回到b中，并返回索引向量i、j。其中，i表示元素在原向量或矩阵中的最大索引位置；j表示原向量中单值元素在b中的索引位置。

A=[8,7,3,9,2,4,11,3,8,4,4];
[b,i,j]=unique(A)

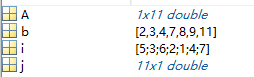
　　③find()

　　功能：找到矩阵数据中相应标识所在的位置。

　　使用格式：[i，j]=find（X=-mark），找到样本矩阵X中和mark值一样的元素，返回它所在的位置，i记录行坐标，j记录列坐标。

　　④isnan()

　　功能：判断矩阵数据中的元素是否为数值。

　　使用格式：Y=isnan（X），对样本矩阵X中的每个元素进行判断，如果元素为数值则返回0，不是数值则返回1，返回的结果存储到矩阵Y中，矩阵Y由0、1组成。

　　⑤mapminmax()

　　功能：对数据矩阵进行最大值、最小值的规范化。

　　使用格式：Z=mapminmax（X，ymin，ymax），输入样本数据X，规范化后的最小值为ymin，最大值为ymax，Z为进行规范化后的数据。

　　eg：将一个10维行向量进行最大值、最小值的规范化到[0，1]之间。

X=1:1:10;
Z=mapminmax(X,0,1)

　　⑥zscore()

　　功能：对数据矩阵进行标准差的规范化。

　　使用格式：Z=zscore(x)，对样本矩阵X进行标准差的标准化，返回标准化后的结果到z矩阵中。

　　⑦pca()

　　功能：对指标变量矩阵进行主成分分析。

　　使用格式：[coeff，score，latent，tsquared]=pca（X）

　　X为要进行主成分分析的数据矩阵，X矩阵一列的值代表一个变量指标的一列观测值。

　　latent为主成分分析得到的特征根；

　　coeff为各特征根对应的系数矩阵；

　　score为得分，由coeff与X得到；

　　tsquared为X中每个观测值的Hotelling's T-squared值

　　eg：使用pca()函数对一个10×4维的随机矩阵进行主成分分析的结果如下。

X=rand(10,4);
[coeff,score,latent]=pca(X)

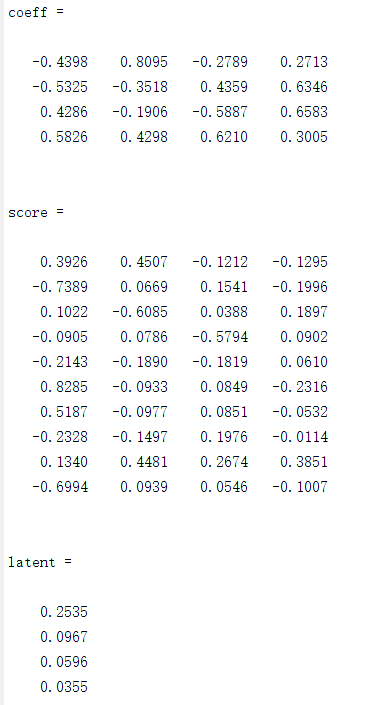
　　⑧rand()

　　功能：生成服从均匀分布的随机矩阵，元素分布在区间（0，1）上，抽样时可使用。

　　使用格式：Y=rand(n)，生成一个n·n随机矩阵，其元素均匀分布在区间（0，1）上；

　　Y=rand(m，n)，生成一个m·n随机矩阵，其元素均匀分布在区间（0，1）上。

　　eg：使用rand函数对一个10维的向量放回采集一个3维样本的代码如下。

a=1:1:10;
m=length(a);
n=3;
idx=ceil(m*rand(1,n));
b=a(idx)

　　⑨randsample()

　　功能：进行不放回随机抽样。

　　使用格式：a=randsample(n，k)，1~n的数字序列里随机返回k个数。

　　其中，这k个数之间彼此不相同，以实现不放回随机抽样。