数据质量、特征分析及一些MATLAB函数

MATLAB数据分析工具箱

　　MATLAB工具箱主要含有的类别有：

　　数学类、统计与优化类、信号处理与通信类、控制系统设计与分析类、图像处理类、测试与测量类、计算金融类、计算生物类、并行计算类、数据库访问与报告类、 MATLAB 代码生成类、 MATLAB 应用发布类。

　　每个类别内含有一个或多个工具箱。

　　比如数学、统计与优化类别就包含有曲线拟合工具箱、优化工具箱、神经网络工具箱、统计工具箱等。

　　MATLAB 应用发布类别主要包含MATLAB和其他语言的混合编译、编程，包括C、C#、Java等。

　　MATLAB 中与数据分析及挖掘相关的工具箱，包含统计工具箱、优化工具箱、曲线拟合工具箱、神经网络工具箱。(这里先大致写一下，后面的文章会专门细写的)

　　统计工具箱可以对数据进行组织、分析和建模，使用和统计分析、机器学习相关的算法及工具。用户可以使用回归以及分类分析来进行预测建模、生成随机序列(蒙特卡罗模拟),同时可 以使用统计分析工具对数据进行前期的探索研究或者进行假设性检验。在分析多维数据时,统计工具箱提供连续特征选择、主成分分析、正规化和收缩、偏最小二乘回归分析法等工具帮助用户筛选出对模型有重要影响的变量。该工具箱同时还提供有监督、无监督的机器学习算法，包括支持向量机(SVMs)、决策树、K- Means、分层聚类、K近邻聚类搜索、高斯混合、隐马尔科夫模型等。

　　优化工具箱主要提供用于在满足给定的束缚条件时寻找最优解的相关函数，主要包含线性规划、混合整数线性规划、二次规划、非线性最优化、非线性最小平方问题的求解函数。 在该工具箱中，用户可以针对连续型、离散型问题寻求最优的解决方法，使用权衡分析法进行分析,或者在算法和应用中融合多种优化方法,从而达到较好的效果。

　　曲线拟合工具箱提供一个图形用户界面和各种函数调用接口供用户实现数据拟合。使用该工具箱可以进行数据探索性分析、数据预处理、数据过程处理、比较分析候选模型和异常值过滤。用户可以使用 MATLAB 库函数提供的线性与非线性模型或者用户自定义的方程式来进行回归分析。该工具箱也支持无参数模型,比如样条变换、插值以及平滑。

　　神经网络工具箱提供的函数以及应用可以用于复杂的、非线性系统的建模。不仅支持前馈监督式学习、径向基和动态网络，同时还支持组织映射以及竞争层形式的非监督式学习。利用该工具箱，用户可以设计、训练、可视化以及仿真神经网络。神经网络工具箱的应用主要包括：回归、分类、聚类分析、时间序列预测和动力系统建模，对应于其所包含的四个子工具箱。在处理海量数据时，还可以考虑使用数据分布式以及分布式计算功能、GPU功能以及并行计算工具箱。

 

数据质量分析

　　数据质量分析主要是检查原始数据中是否存在脏数据，脏数据一般是指不符合要求，以及不能直接进行相应分析的数据，常见的有缺失值、异常值、不一致的值、重复数据及含有特殊符号的数据。

缺失值与异常值分析

　　这里，我们以餐饮销量数据为例，检测分析其缺失值及异常值。

　　

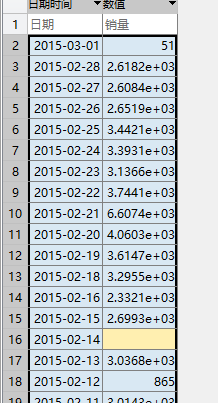
%% 餐饮销量数据缺失值及异常值检测
clear;
catering_sale = '../data/catering_sale.xls'; % 餐饮数据
index = 1; % 销量数据所在列 
%% 读入数据
[num,txt] = xlsread(catering_sale);
sales =num(2:end,index);
rows = size(sales,1);
%% 缺失值检测 并打印结果
nanvalue = find(isnan( sales));
if isempty(nanvalue) %  没有缺失值
    disp('没有缺失值！');
else
    rows_ = size(nanvalue,1);
    disp(['缺失值个数为：' num2str(rows_) ',缺失率为：' num2str(rows_/rows) ]);
end
%% 异常值检测 
% 箱形图上下界
q_= prctile(sales,[25,75]);
p25=q_(1,1);
p75=q_(1,2);
upper = p75+ 1.5*(p75-p25);
lower = p25-1.5*(p75-p25);
upper_indexes = sales(sales>upper);
lower_indexes = sales(sales<lower);
indexes =[upper_indexes;lower_indexes];
indexes = sort(indexes);
% 箱形图
figure
hold on;
boxplot(sales,'whisker',1.5,'outliersize',6);
rows = size(indexes,1);
flag =0;
for i =1:rows
  if flag ==0
    text(1+0.01,indexes(i,1),num2str(indexes(i,1)));
    flag=1;
  else
      text(1-0.017*length(num2str(indexes(i,1))),indexes(i,1),num2str(indexes(i,1)));
    flag=0;
  end
end
hold off;
disp('餐饮销量数据缺失值及异常值检测完成！');

　　得到结果：

　　与箱形图：

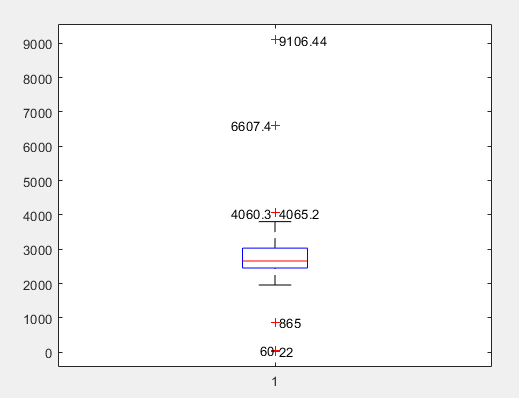
 　　箱形图补充：

　　　　

　　对于箱形图，必须要提及四分位数的概念。

　　人们经常会将数据划分为4个部分，每一个部分大约包含有1/4即25％的数据项。这种划分的临界点即为四分位数。它们定义如下。
　　Q1=第1四分位数，即第25百分位数；Q2=第2四分位数，即第50百分位数；Q3=第3四分位数，即第75百分位数。这些可以通过箱形图直观的看出来。

　　下限 < 下四分位数 < 中位数 < 上四分位数 < 上限

箱形图的意义：
①直观明了地识别数据批中的异常值。
②利用箱线图判断数据批的偏态和尾重。
对于标准正态分布的样本，只有极少值为异常值。异常值越多说明尾部越重，自由度越小。
③利用箱线图比较几批数据的形状
同一数轴上，几批数据的箱线图并行排列，几批数据的中位数、尾长、异常值、分布区间等形状信息便昭然若揭。

缺点：
不能精确地衡量数据分布的偏态和尾重程度；对于批量比较大的数据，反映的信息更加模糊以及用中位数代表总体评价水平有一定的局限性......

　　从图中可以读出离群点(异常值)，即被圈住的那些：

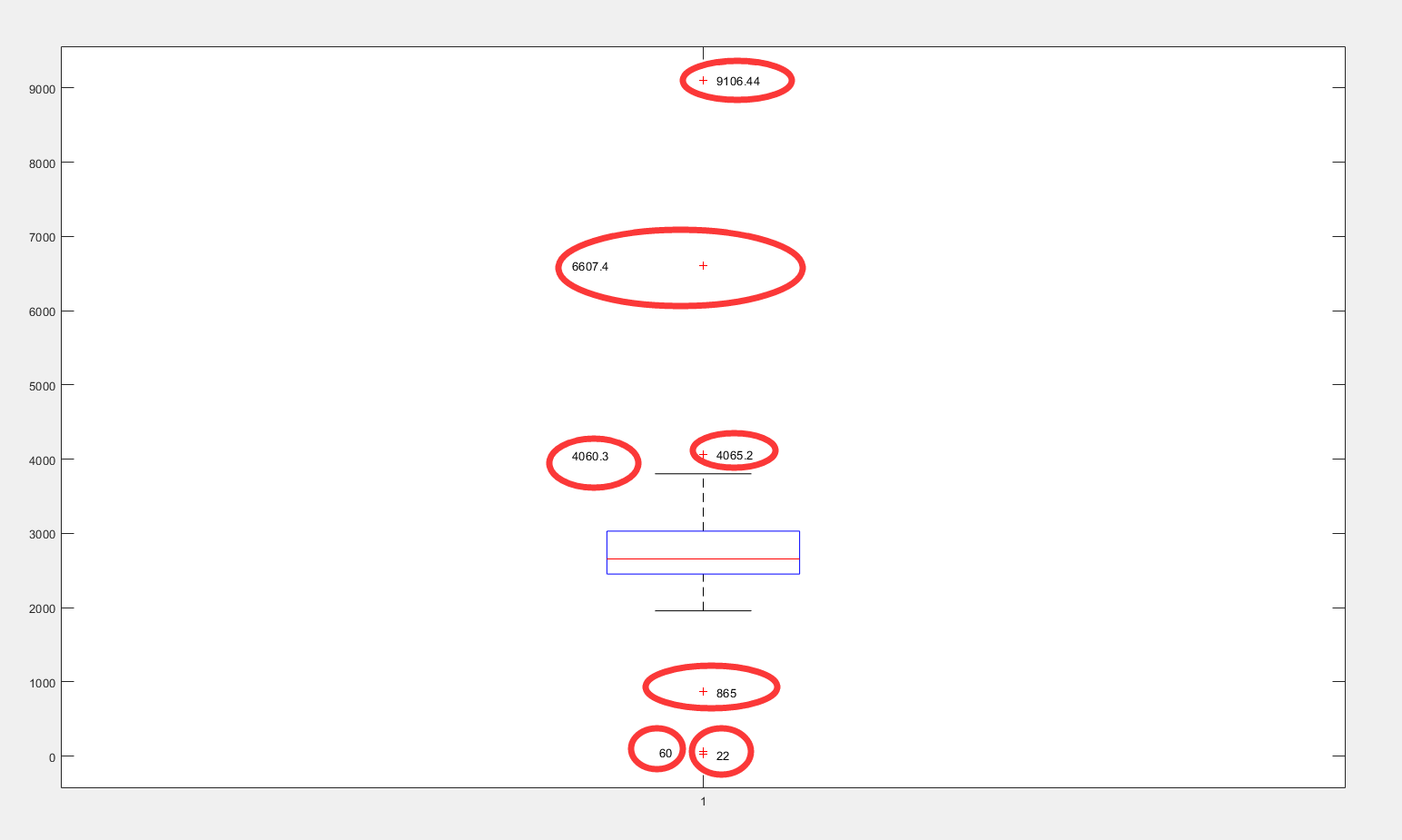
　　从箱形图我们可以看出，超过上下界存在7个数据可能为异常值，结合具体业务，可以把865、4060.3、4065.2归为正常值，将60、22、6607.4、9106.44归为异常值。最后确定过滤规则为日销量在400以下或5000以上属于异常数据。

缺失值处理

　　数据清洗主要包括缺失值处理、异常值处理。

　　处理缺失值的方法可以分为三类：删除记录、数据插补和不处理。其中，插补最常用。
　　插补方法有：均值/中位数/众数插补、使用固定值、最近临插补、回归方法、插值法。

　　插值法请参考另一篇blog：https://www.cnblogs.com/fangxiaoqi/p/11437444.html

　　下面用拉格朗日插值法与牛顿插值法对缺失值进行插补：(当然有很多更好的方法)

%% 拉格朗日插值和牛顿插值对比
clear;
% 参数初始化
inputfile = '../data/catering_sale.xls' ; % 销量数据文件
index =1; % 销量数据所在下标
outputfile ='../tmp/sales.xls';  % 插值后数据存放
%% 读入数据
[num,txt,raw] = xlsread(inputfile);
data = num(:,index);
%% 去除异常值
data = de_abnormal(data);
%% 调用拉格朗日进行插值
la_data = ployinterp_column(data,'lagrange');
%% 调用牛顿算进行插值
new_data = ployinterp_column(data,'newton');
%% 结果写入文件
rows = size(data,1);
result = cell(rows+1,3);
result{1,1}='原始值';
result{1,2}='拉格朗日插值';
result{1,3}='牛顿插值';
result(2:end,1)= num2cell(data);
result(2:end,2)= num2cell(la_data);
result(2:end,3)= num2cell(new_data);
xlswrite(outputfile,result);
disp('拉格朗日插值和牛顿插值结果已写入数据文件！');

function outputdata= ployinterp_column(columndata,type)
%% 针对每列进行插值
% 输入参数说明：
% columndata: 输入的列数据，含有缺失值
% type: 'lagrange' 或'newton' 
% 输出参数说明：
% output: 输出插值过的数据
%% 把输入列数据分为非缺失值和缺失值数据
nans = isnan(columndata);  %  区分columndata中为NaN的数据下标
notzeroIndexes = find(nans); % 寻找缺失值下标
%zeroIndexes = find(nans==0); % 寻找非缺失值下标
rows=size(columndata); %原始数据的行数 
%currentValues=zeros(size(zeroIndexes));% 初始化当前值矩阵
for i=1:size(notzeroIndexes)
    pre5=findPre5(notzeroIndexes(i),columndata);
    last5=findLast5(notzeroIndexes(i),rows(1),columndata);
    [~,pre5cols]=size(pre5);
    [~,last5cols]=size(last5);
    if   strcmp(type,'lagrange')
missingValue=lagrange_interp([1:pre5cols,pre5cols+2:last5cols+pre5cols+1],...
            [pre5,last5],pre5cols+1); % 拉格朗日插值
    else
missingValue=newton_interp([1:pre5cols,pre5cols+2:last5cols+pre5cols+1],...
            [pre5,last5],pre5cols+1); % 牛顿插值
    end
    columndata(notzeroIndexes(i),1)=missingValue;
end
% 返回插值后的数据
outputdata=columndata;
end

function pre5=findPre5(index,columndata)
%% 在columndata中寻找给定下标index前面5个数值（非NaN），不足5个的按实际情况返回
if index<=0
    disp('非法下标');
    exit; 
end
num=5;
pre5=nan(1,5);
for i=index-1:-1:1
    if isnan(columndata(i))==0  % 判断第i个值是否为NaN
        pre5(num)=columndata(i);
        num=num-1;
    end
    if num==0 % 只取前5个
        break;
    end
end
pre5=pre5(~isnan(pre5)); % 去除NaN的值
end 
function last5=findLast5(index,rows,columndata)
%% 在columndata中寻找给定下标index后面5个数值（非NaN），不足5个的按实际情况返回
if index<=0 || index>rows
    disp('非法下标');
    exit; 
end
num=0;
last5=nan(1,5); % 初始化
for i=index+1:rows
    if isnan(columndata(i))==0  % 判断第i个值是否为NaN
        num=num+1;
        last5(num)=columndata(i); 
    end
    if num==5 % 只取后5个
        break;
    end
end
last5=last5(~isnan(last5)); % 去除NaN的值
end

　　从结果中，我们可以看出，在插值前会对数据进行异常值检测，发现的一些异常数据会定义为空缺值，也会进行补数。

异常值处理

在数据预处理时，异常值是否剔除，需要视具体情况而定，因为有些异常值可能蕴含着有用的信息。
异常值处理的常用方法有：
①删除含有异常值的记录
将含有异常值的记录直接删除这种方法简单易行，但缺点也很明显，在观测值很少的情况下，删除会导致样本量不足，可能会改变原有的分布，从而造成分析结果不准确。
②视为缺失值
视为缺失值可以利用现有变量的信息，对异常值进行填补。
③平均值修正
④不处理
一般先分析异常值出现的可能原因，再判断是否舍弃，如果是正确的数据，可以直接在具有异常值的数据集上进行挖掘建模。

数据特征分析

对比分析

　　对比分析是指把两个相互联系的指标进行比较，从数量上展示和说明研究对象规模的大小、水平的高低、速度的快慢，以及各种关系是否协调。特别适用于指标间的横纵向比较、时间序列的比较分析。在对比分析中，选择合适的对比标准是十分关键的步骤，选择得合适，才能作出客观的评价，选择不合适，评价可能会得出错误的结论。

　　对比分析主要有以下两种形式。

　　1、绝对数比较

　　它是利用绝对数进行对比，从而寻找差异的一种方法。

　　2、相对数比较

　　它是用两个有联系的指标对比计算的，用以反映客观现象之间数量联系程度的综合指标，其数值表现为相对数。

　　由于研究目的和对比基础不同，相对数可以分为以下几种：

　　　　①结构相对数：将同一总体内的部分数值与全部数值对比求得比重，用以说明事物的性质、结构或质量。如居民食品支出额占消费支出总额的比重、产品合格率等。

　　　　②比例相对数：将同一总体内不同部分的数值对比，表明总体内各部分的比例关系，如人口性别比例、投资与消费比例等。

　　　　③比较相对数：将同一时期两个性质相同的指标数值对比，说明同类现象在不同空间条件下的数量对比关系。如不同地区商品价格的对比；不同行业、不同企业间某项指标的对比等。

　　　　④强度相对数：将两个性质不同但有一定联系的总量指标对比，用以说明现象的强度、密度和普遍程度。如人均国内生产总值用“元/人”表示，人口密度用“人/平方公里”表示，也有用百分数或千分数表示的，如人口出生率用%。表示。

　　　　⑤计划完成程度相对数：是某一时期实际完成数与计划数进行对比，用以说明计划完成的程度。

统计量分析

　　用统计指标对定量数据进行统计描述，常从集中趋势和离中趋势两个方面进行分析。
　　集中趋势：平均水平的指标是对个体集中趋势的度量，使用最广泛的是均值和中位数；
　　离中趋势：反映变异程度的指标则是个体离开平均水平的度量，使用较广泛的是标准差、方差、四分位间距。

1、集中趋势度量

①均值

　　原始观察数据平均值：$$\operatorname{mean}(x)=\overline{x}=\frac{\sum x_{i}}{n}$$
　　加权均值：$$\operatorname{mean}(x)=\overline{x}=\frac{\sum w_{i} x_{i}}{\sum w_{i}}=\frac{w_{1} x_{1}+w_{2} x_{2}+\ldots+w_{n} x_{n}}{w_{1}+w_{2}+\dots+w_{n}}$$
　　为了消除少数极端值的影响，可以使用截断均值或者中位数来度量数据的集中趋势。

②中位数

③众数

众数是指数据集中出现最频繁的值，众数并不经常用来度量定性变量的中心位置，其更适用于定性变量。

2、离中趋势度量
①极差

　　极差=最大值-最小值

②标准差

标准差度量数据偏离均值的程度

③变异系数

变异系数度量标准差相对于均值的离中趋势，计算公式为：$$CV = \frac{s}{{\bar x}} \times 100{\rm{\% }}$$
变异系数主要用来比较两个或多个具有不同单位或不同波动幅度的数据集的离中趋势。

④四分位数间距

四分位数间距是上四分位数与下四分位数之差，其间包括了全部观察值的一半，其值越大，说明数据的变异程度越大，反之说明数据的变异程度越小。

%% 餐饮销量数据统计量分析
clear;
% 初始化参数
catering_sale = '../data/catering_sale.xls'; % 餐饮数据
index = 1; % 销量数据所在列 
%% 读入数据
[num,txt] = xlsread(catering_sale);
sales = num(2:end,index);
sales = de_missing_abnormal(sales,index);
%% 统计量分析
% 均值
mean_ = mean(sales);
% 中位数
median_ = median(sales);
% 众数
mode_ = mode(sales);
% 极差
range_ = range(sales);
% 标准差
std_ = std(sales);
% 变异系数
variation_ = std_/mean_;
% 四分位数间距
q1 = prctile(sales,25);
q3 = prctile(sales,75);
distance = q3-q1;
%% 打印结果
disp(['销量数据均值：' num2str(mean_) ',中位数：' num2str(median_) ',众数:' ...
    num2str(mode_) ',极差：' num2str(range_) ',标准差：' num2str(std_) ...
    ',变异系数：' num2str(variation_) ',四分位间距：' num2str(distance)]);
disp('餐饮销量统计量分析完成！');

function [ output ] = de_missing_abnormal( sales,index )
%%  去缺失值和异常值
% 去缺失值
nanvalue_ = ~isnan( sales(:,index));
sales =sales(nanvalue_,:);
% 去缺失值
abnormalvalue_ = sales(:,index)>=400;
sales = sales(abnormalvalue_,:);
abnormalvalue_ = sales(:,index) <=5000;
output = sales(abnormalvalue_,:);
end

 

贡献度分析

　　贡献度分析又称帕累托分析，原理是帕累托法则，它是指在任何特定群体中，重要的因子通常只占少数，而不重要的因子则占多数，因此只要能控制具有重要性的少数因子即能控制全局。

　　以餐饮系统对应的菜品盈利数据为例：

　　

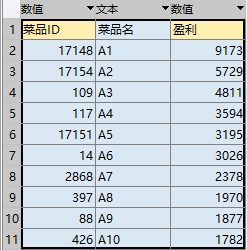
%% 菜品盈利数据 帕累托图
clear;
% 初始化参数
dish_profit = '../data/catering_dish_profit.xls'; % 餐饮菜品盈利数据
%% 读入数据
[num,txt,raw] = xlsread(dish_profit);
%% 帕累托图作图
rows = size(num,1);
hold on;
% 计算累计系数
yy_ = cumsum(num(:,end));
yy=yy_/yy_(end)*100;
[hAx,hLine1,hLine2]=plotyy(1:rows,num(:,end),1:rows,yy,'bar','plot');
set(hAx(1),'XTick',[])%去掉x轴的刻度
set(hLine1,'BarWidth',0.5);
set(hAx(2), 'XTick', 1:rows);  
set(hAx(2),'XTickLabel',raw(2:end,2));
ylabel(hAx(1),'盈利：元') % left y-axis
ylabel(hAx(2),'累计百分比：%') % right y-axis
set(hLine2,'LineStyle','-')
set(hLine2,'Marker','d')
% 标记 80% 点
index = find(yy>=80);
plot(index(1),yy(index(1))*100,'d', 'markerfacecolor', [ 1, 0, 0 ] );
text(index(1),yy(index(1))*93,[num2str(yy(index(1))) '%'] );
hold off;
disp('餐饮菜品盈利数据帕累托图作图完成！');

　　

相关性分析

　　分析连续变量之间线性相关程度的强弱，并用适当的统计指标表示出来的过程被称为相关性分析。
　　1、直接绘制散点图(最直观判断线性关系)
　　2、绘制散点图矩阵
　　需要同时考虑多个变量之间的相关关系是，一一绘制其简单散点图会十分麻烦。此时可以利用散点图矩阵来同时绘制各变量间的散点图，从而快速发现多个变量间的主要相关性。

　　

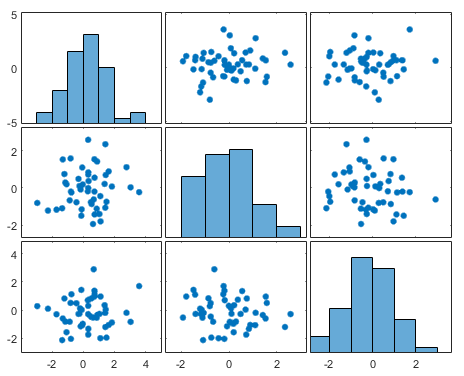
　　3、计算相关系数
　　①Pearson相关系数

　　皮尔森相关系数是用来反映两个变量线性相关程度的统计量。相关系数用 r 表示，r 描述的是两个变量间线性相关强弱的程度。r 的绝对值越大表明相关性越强。

　　一般用于分析两个连续性变量之间的关系，其公式如下：

$$r = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)} \left( {{y_i} - \bar y} \right)}}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} \sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} } }}{\rm{,  - 1}} \le r \le 1$$　　

　　②Spearman秩相关系数

　　由于皮尔逊相关系数有两个局限：①必须假设数据是成对地从正态分布中取得的。②数据至少在逻辑范围内是等距的。所以，对于更一般的情况，Spearman秩相关系数更常用，而且这是一种无参检验方法(与分布无关)。

　　在统计学中，以查尔斯·斯皮尔曼命名的斯皮尔曼等级相关系数，即Spearman相关系数。经常用希腊字母p表示。它是衡量两个变量的依赖性的非参数指标。它利用单调方程评价两个统计变量的相关性。如果数据中没有重复值，并且当两个变量完全单调相关时，斯皮尔曼相关系数则为+1或-1。

　　Pearson线性相关系数要求连续变量的取值服从正态分布，而不服从正态分布的变量、分类或等级变量之间的关联性可采用Spearman秩相关系数来描述，也可以理解为等级变量之间的皮尔逊相关系数。。

　　其计算公式为：$$ρ=1-\frac{6 \sum_{i=1}^{n}\left(R_{i}-Q_{i}\right)^{2}}{n\left(n^{2}-1\right)}$$

　　${R_i}$代表${x_i}$的秩次，${Q_i}$代表${y_i}$的秩次，${R_i} - {Q_i}$为${x_i},{y_i}$的秩次之差，$n$表示样本数。

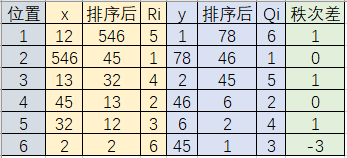
　　如图，计算得到$$p = 1 - \frac{{6*(1 + 1 + 1 + 9)}}{{6*(36 - 1)}} = 0.6571$$

　　因为一个变量的相同的取值必须有相同的秩次，所以在计算中采用的秩次是排序后所在位置的平均值。

　　易知，只要两个变量具有严格单调的函数关系，那么它们就是完全Spearman相关的，这与Pearson相关不同，Pearson 相关只有在变量具有线性关系时才是完全相关的。

　　上述两种相关系数在实际应用计算中都要对其进行假设检验，使用 t 检验方法检验其显著性水平以确定其相关程度。

　　研究表明，在正态分布假设下，Spearman秩相关系数与Peatson相关系数在效率上是等价的，而对于连续测量数据，更适合用Pearson相关系数来进行分析。 

　　③判定系数

　　判定系数是相关系数的平方，用${r^2}$表示，用来衡量回归方程对y的解释程度。

　　判定系数的取值范围：0≤${r^2}$≤1。

　　${r^2}$越接近1，表明x与y之间的相关性越强；${r^2}$越接近0，表明两个变量之间几乎没有直线相关关系。

%% 餐饮销量数据相关性分析
clear;
% 初始化参数
catering_sale = '../data/catering_sale_all.xls'; % 餐饮数据，含有其他属性
index = 1; % 销量数据所在列 
%% 读入数据
[num,txt] = xlsread(catering_sale);
%% 相关性分析
corr_ = corr(num);
%% 打印结果
rows = size(corr_,1);
for i=2:rows
    disp(['"' txt{1,2} '"和"' txt{1,1+i} '"的相关系数为：' num2str(corr_(i,1))]);
end
disp('餐饮菜品日销量相关性分析完成！');

　　分析这些菜品销售量之间的相关性可以得到不同菜品之间的关系，比如是替补菜品、互补菜品或者没有关系的菜品，为原材料采购提供参考。  

　　从上面的结果可以看到如果顾客点了“百合酱蒸凤爪”和点“翡翠蒸香茜饺”“金银蒜汁蒸排骨”“香煎萝卜糕”“铁板酸菜豆腐”“香煎韭菜饺”等主食类的相关性比较低，反而点“乐膳真味鸡”“生炒菜心”“原汁原味菜心”的相关性比较高。

MATLAB主要数据的探索函数

特征统计函数

　　①mean

　　功能：计算数据样本的算术平均值。

　　使用格式：n=mean(X)

　　②geomean

　　功能：计算数据样本的几何平均数。

　　使用格式：n=geomean(X)

　　③var

　　功能：计算数据样本的方差。

　　使用格式：v=var(X)

　　④std

　　功能：计算数据样本的标准差。

　　使用格式：s=std(X)

　　⑤corr

　　功能：计算数据样本的Spearman(Pearson)相关系数矩阵。

　　使用格式：R=corr(x,y,'name',value)

x=[1:8]';
y=[2:9]';
R=corr(x,y,'type','Spearman')

 

　　⑥cov

　　功能：计算数据样本的协方差矩阵。

　　使用格式：R=cov(X)。

X=randn(20,5);
R=cov(X)

　　⑦moment

　　功能：计算数据样本的指定阶中心距。

　　使用格式：m=moment(X，order) % 计算样本X的order阶次的中心距m。

X=randn(20,5);
m=moment(X,2)

 

 

统计作图函数

　　通过统计作图函数绘制的图表可以直观地反映出数据及统计量的性质及其内在的规律，如盒图可以表示多个样本的均值，误差条形图能同时显示下限误差和上限误差，最小二乘拟合曲线图能分析两个变量间的关系。

　　①plot

　　功能：绘制线性二维图、折线图。

　　使用格式：plot（x，y，S），S指定绘制时图形的类型、样式、颜色，常用的选项有：‘b’为蓝色、“r’为红色、g’为绿色、‘o’为圆圈、‘+’为加号标记、’为实线、-’为虚线。

　　②pie

　　功能：绘制饼形图。

　　使用格式：pie（x），绘制矩阵x中非负数据的饼形图。

　　若x中非负元素和小于1，则函数仅画出部分饼形图，且非负元素X(i，j)的值直接限定饼形图中扇形的大小；

　　若X中非负元素和大于等于1，则非负元素X(i，j)代表饼形图中的扇形大小通过X(i，j)/Y的大小来决定。其中，Y为矩阵X中非负元素和。

x=[1,3,1.5,4,1.5];
explode=[1,0,0,0,0];
pie(x,explode)

　　③hist

　　功能：绘制二维条形直方图，可显示数据的分布情形。

　　使用格式：N=hist（，X），把向量Y中元素分到由向量X中元素指定中心位置的条形中，且返回每一个条形中的元素个数给向量N。

x=0.05:0.1:0.55;
y=[0.01,0.02,0.03,0.15,0.2,0.25,0.28,0.3,0.31,0.4,0.41,0.5];
hist(y,x)

　　④boxplot

　　功能：绘制样本数据的箱型图。

　　使用格式：boxplot（X，notch）绘制矩阵样本X的箱型图。

　　参数notch=1时，绘制矩阵样本X的带刻槽的凹盒图。参量notch=0时，绘制矩阵样本X的无刻槽的矩形箱型图。

　　例如，绘制样本数据的箱型图，样本由两组正态分布的随机数据组成，一组数据均值为4，标准差为5，另一组数据均值为8，标准差为6。

x1=normrnd(4,5,100,1);
x2=normrnd(8,6,100,1);
boxplot([x1,x2],1)

　　⑤semilogx/semilogy
　　功能：绘制x或y轴的对数图形。
　　使用格式：semilogx(x，y)，对x轴使用对数刻度(以10为底)，y轴使用线性刻度，进行plot函数绘图，等价于plot(log10(x)，y)

x=0:1000;
y=log(x);
figure
subplot(2,2,1)
plot(x,y);
title('semilogx原始数据图');
subplot(2,2,3)
semilogx(x,y);
title('semilogx转换图');
x=0:0.1:10;
y=exp(x);
subplot(2,2,2)
plot(x,y)
title('seailogy 原始数据图');
subplot(2,2,4)
semilogy(x,y);
title('semilogy 转换图');

　　⑥errorbar
　　功能：绘制误差条形图。
　　使用格式：errorbar(X，Y，L，U)，绘制误差条形图。
　　参量X、Y、I、U必须为同型向量或矩阵。
　　若同为向量，则在点(X(i)，Y(i))处画出向下长为L(i)，向上长为U(i)的误差棒；
　　若同为矩阵，则在点(X(i,j)，Y(i,j))处画出向下长为L(i,j)，向上长为U(i,j)的误差棒。

X=0:pi/10:pi;
Y=2*X.*sin(X);
E=std(Y)*ones(size(X));
errorbar(X,Y,E,E)