BP神经网络
人工神经网络与人工神经元模型
In machine learning and cognitive science, artificial neural networks (ANNs) are a family of statistical learning models inspired by biological neural networks (the central nervous systems of animals, in particular the brain) and are used to estimate or approximate functions that can depend on a large number of inputs and are generally unknown.
在机器学习和认知科学,人工神经网络(ann)是一个家庭的统计学习模型受生物神经网络(动物的中枢神经系统,特别是大脑)和用于估计或近似函数,可以依靠大量的输入和通常是未知的。
人工神经网络是人工智能研究的一种方法。实际上人工神经网络(Artificial Neural Netwroks,简称ANN)是对人类大脑系统的一种仿真,简单地讲,它是一个数学模型,可以用电子线路来实现,也可以用计算机程序来模拟,由大量的、功能比较简单的形式神经元互相连接而构成的复杂网络系统,用它可以模拟大脑的许多基本功能和简单的思维方式。尽管它还不是大脑的完美无缺的模型,但它可以通过学习来获取外部的知识并存贮在网络内,可以解决计算机不易处理的难题,特别是语音和图像的识别、理解、知识的处理、组合优化计算和智能控制等一系列本质上是非计算的问题。
生物神经元:
生物神经元模型就是一个简单的信号处理器。树突是神经元的信号输入通道,接受来自其他神经元的信息。轴突是神经元的信号输出通道。
信息的处理与传递主要发生在突触附近。神经元细胞体通过树突接受脉冲信号,通过轴突传到突触前膜。当脉冲幅度达到一定强度,即超过其阈值电位后,突触前膜将向突触间隙释放神经传递的化学物质(乙酰胆碱),使位于突触后膜的离子通道(Ion Channel)开放,产生离子流,从而在突触后膜产生正的或负的电位,称为突触后电位。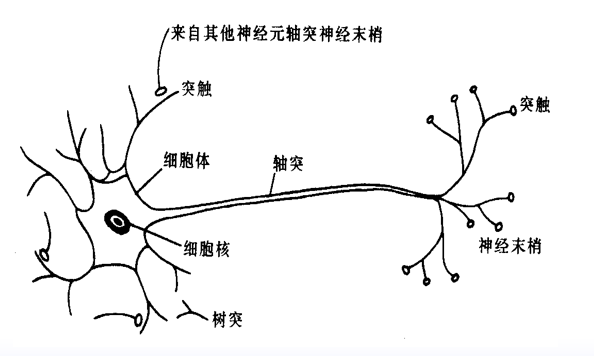
突触有两种:兴奋性突触和抑制性突触。前者产生正突触后电位,后者产生负突触后电位。一个神经元的各树突和细胞体往往通过突触和大量的其他神经元相连接。这些突触后电位的变化,将对该神经元产生综合作用,即当这些突触后电位的总和超过某一阎值时,该神经元便被激活,并产生脉冲,而且产生的脉冲数与该电位总和值的大小有关。脉冲沿轴突向其他神经元传送,从而实现了神经元之间信息的传递。
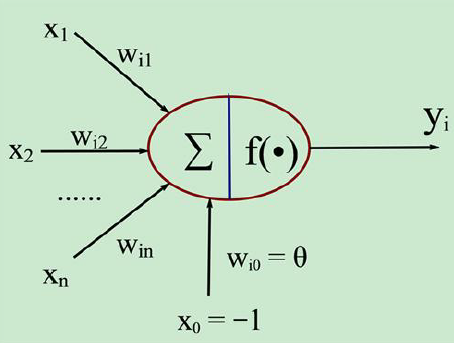
人工神经元模型的三要素:
①连接权ω ②求和单元∑ ③激活函数f(·)
其中,
$X=[ \times 0, \times 1, \times 2, \ldots \ldots ., \times n]$ $\mathbf{W}=\left[\begin{array}{c}{w_{10}} \\ {w_{i 1}} \\ {w_{i 2}} \\ {\vdots} \\ {w_{i n}}\end{array}\right]$
常用表达式一:
$\begin{array}{c}{\text { net }_{i}=\sum_{j=1}^{n} w_{i j} x_{j}-\theta} \\ {y_{i}=\mathrm{f}\left(\text { net }_{i}\right)}\end{array}$
常用表达式二:
$\begin{array}{c}{\text { net }_{i}=\mathrm{XW}} \\ {y_{i}=\mathrm{f}\left(\mathrm{net}_{i}\right)=\mathrm{f}(\mathrm{XW})}\end{array}$
常用的激活函数:
①线性函数
$$\mathrm{f}(\mathrm{x})=k * x+c$$
②斜坡函数
$$f(x)=\left\{\begin{array}{cc}{T} & {, \quad x>c} \\ {k * x,} & {|x| \leq c} \\ {-T,} & {x<-c}\end{array}\right.$$
③阈值函数
$$f(x)=\left\{\begin{array}{l}{1, x \geq c} \\ {0, x<c}\end{array}\right.$$
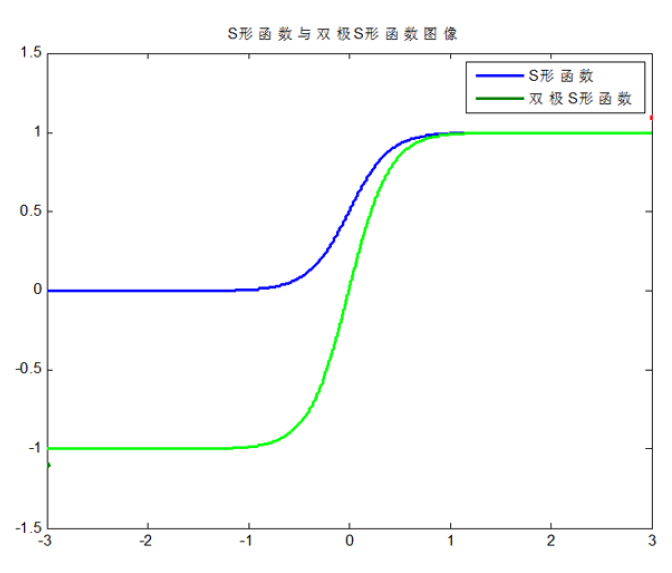
④S型函数(Sigmoid)
$$\begin{array}{c}{f(x)=\frac{1}{1+e^{-\alpha x}}(0<f(x)<1)} \\ {f^{\prime}(x)=\frac{\alpha e^{-\alpha x}}{\left(1+e^{-\alpha x}\right)^{2}}=\alpha f(x)[1-f(x)]}\end{array}$$
⑤双极S型函数
$$\begin{array}{l}{f(x)=\frac{2}{1+e^{-\alpha x}}-1(-1<f(x)<1)} \\ {f^{\prime}(x)=\frac{2 \alpha e^{-\alpha x}}{\left(1+e^{-\alpha x}\right)^{2}}=\frac{\alpha\left[1-f(x)^{2}\right]}{2}}\end{array}$$
神经网络
连接方式
按照连接方式,可划分为前向神经网络与反馈(递归)神经网络。
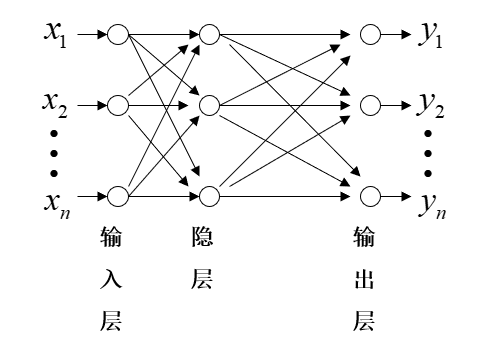
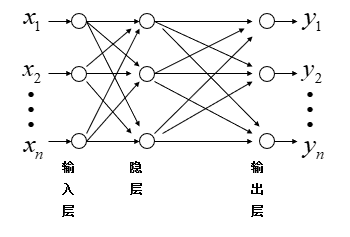
前向神经网络:
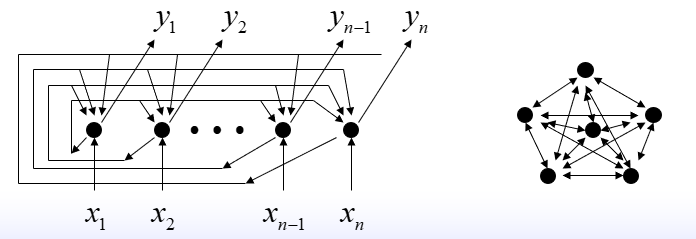
反馈神经网络:
学习方式
按照连接方式,可分为有导师学习神经网络与无导师学习神经网络。
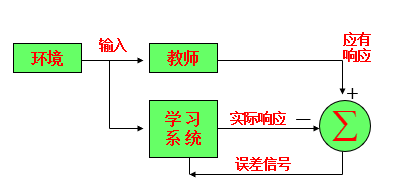
有导师学习神经网络:
外界存在一个教师,对给定的一组输入,提供应有的输出(标准答案),学习系统可根据实际输出与标准答案之间的差值来调整系统参数。
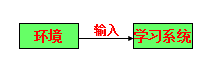
无导师学习神经网络:
学习系统按照环境提供数据的某些统计规律来调节自身参数。
♦强化学习:
环境对系统输出结果只给出评价信息(奖或惩),系统通过强化受奖动作来改善自身性能。
学习规则
考察神经元 k 在 n 时刻的输入和输出。
输入: $x_{k}(n)$
实际输出: $y_{k}(n)$
理应输出: $d_{k}(n)$
误差信号: $e_{k}(n)=d_{k}(n)-y_{k}(n)$
由误差信号构造能量函数: $J(\omega)=E\left[\frac{1}{2} \sum_{k} e_{k}^{2}(n)\right]$。其中,$E( .)$为求期望算子。
求解最优化问题: $\min _{\omega} J(\omega)=E\left[\frac{1}{2} \sum_{k} e_{k}^{2}(n)\right]$
得出系统参数: ω
通常情况下用时刻 n 的瞬时值 $J_{n}(\omega)=\frac{1}{2} \sum_{k} e_{k}^{2}(n)$ 代替$J$。
即求解最优化问题: $\min _{\omega} J_{n}(\omega)=\frac{1}{2} \sum_{k} e_{k}^{2}(n)$
由数值迭代算法(如最速下降法、模拟退火算法等),可得 $\Delta \omega_{k j}=\eta e_{k}(n) x_{j}(n)$ 。其中 $\eta$ 为学习步长。
♦Hebb学习规则
神经学家Hebb提出的学习规则:当某一连接两端的神经元同步激活(或同为抑制)时,该连接的强度应增强,反之应减弱,数学描述如下:
$\Delta \omega_{k j}=F\left(h_{k}(n), h_{j}(n)\right)$
其中,$h_{k}(n), h_{j}(n)$ 分别为 $\omega_{i j}$ 两端神经元的状态。
最常用的一种情况是: $\Delta \omega_{k j}=\eta h_{k}(n) h_{j}(n)$
BP神经网络(向后传播算法)
Backpropagation is a common method of teaching artificial neural networks how to perform a given task.
It is a supervised learning method, and is a generalization of the delta rule. It requires a teacher that knows, or can calculate, the desired output for any input in the training set.
Backpropagation requires that the activation function used by the artificial neurons (or "nodes") be differentiable.
反向传播是教授人工神经网络如何执行给定任务的一种常用方法。
它是一种监督学习方法,是delta规则的推广。它要求教师知道或能够计算出训练集中任何输入所需的输出。
反向传播要求人工神经元(或“节点”)使用的激活函数是可微的。
对于多层网络,由于有隐层后学习比较困难,限制了多层网络的发展,BP算法的出现解决了这一困难。
BP算法的原理
对于多层前馈型网络,网络中有两种信号在流通。
①工作信号,施加的输入信号向前传播直到在输出层产生实际的输出信号,是输入信号和权值的函数。
②误差信号,网络实际输出与应有输出间的差值,它由输出层开始逐层向后传播。
BP网络的过程描述:
假设训练样本集为:
$$\left\{\left(x_{p}, t_{p}\right) ; x_{p}=\left(x_{p 1}, \ldots, x_{p N}\right)^{T}, t_{p}=\left(t_{p 1}, \ldots, t_{p M}\right)^{T}, p=1,2, \cdots, \Pi\right\}$$
其中 Π 表示样本集中样本个数,$\mathbb{x}_{p}$为输入向量,$\mathbb{t}_{p}$为输出向量。
BP网络主要有两个阶段:
①信号前传阶段

②误差后传阶段

推导用于多层前馈型网络学习的BP算法
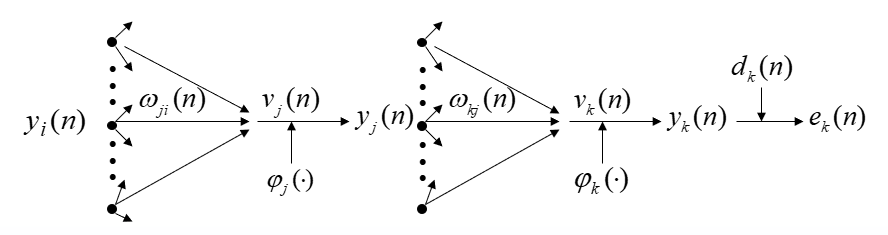
设在第 n 次迭代中某一层的第 j 个单元的输出为 $y_{j}(n)$。
当 j 单元所在层为输出层时,
该单元的误差信号为 $e_{j}(n)=d_{j}(n)-y_{j}(n)$,定义单元 j 的平方误差为 $\frac{1}{2} e_{j}^{2}(n)$,则输出层总的平方误差的瞬时值为: $\xi(n)=\frac{1}{2} \sum_{j} e_{j}^{2}(n)$
下面就逐个样本学习的情况来推导BP算法。
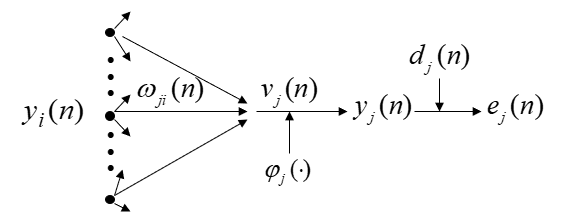
如图,令单元 j 的净输入为 $v_{j}(n)=\sum_{i} \omega_{j i}(n) y_{i}(n)$,则 $y_{j}(n)=\varphi_{j}\left(v_{j}(n)\right)$。
求 $\xi(n)$ 对 $\omega_{j i}$ 的梯度
$\begin{aligned} \frac{\partial \xi(n)}{\partial \omega_{j i}} &=\frac{\partial \xi(n)}{\partial e_{j}(n)} \cdot \frac{\partial e_{j}(n)}{\partial y_{j}(n)} \cdot \frac{\partial y_{j}(n)}{\partial v_{j}(n)} \cdot \frac{\partial v_{j}(n)}{\partial \omega_{j i}(n)}=e_{j}(n) \cdot(-1) \cdot \varphi_{j}^{\prime}\left(v_{j}(n)\right) \cdot y_{i}(n) \\ &=-e_{j}(n) \varphi_{j}^{\prime}\left(v_{j}(n)\right) y_{i}(n) \end{aligned}$
权值 $\omega_{j i}$ 的修正量为 $\Delta \omega_{j i}=-\eta \frac{\partial \xi(n)}{\partial \omega_{j i}(n)}=\eta \delta_{j}(n) y_{i}(n)$
其中 ${\delta _j}(n) = - \frac{{\partial \xi (n)}}{{\partial {e_j}(n)}} \cdot \frac{{\partial {e_j}(n)}}{{\partial {y_j}(n)}} \cdot \frac{{\partial {y_j}(n)}}{{\partial {v_j}(n)}} = {e_j}(n){\varphi _j}^\prime ({v_j}(n))$ 称为局部梯度
当 j 单元所在层为隐层时,
权值${\omega _{ji}}$的修正量为 $${\omega _{ji}} = - \eta \frac{{\partial \xi \left( n \right)}}{{\partial {\omega _{ji}}\left( n \right)}} = \eta {\delta _j}\left( n \right){y_i}\left( n \right)$$
其中,
${\delta _j}(n) = {\varphi _j}^\prime ({v_j}(n))\sum\limits_k {{\delta _k}(n){\omega _{kj}}(n)} $
${\delta _k}(n) = {e_k}(n){\varphi _k}^\prime ({v_k}(n))$
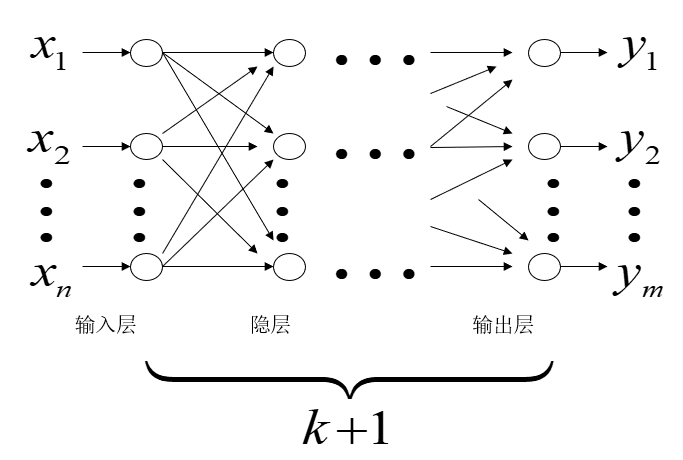
构造多层前向神经网络
BP神经网络的优缺点

MATLAB实现
训练集/测试集产生
1. 导入数据
2. 随机产生训练集和测试集
temp = randperm(size(NIR,1));
% 训练集——50个样本
P_train = NIR(temp(1:50),:)';
T_train = octane(temp(1:50),:)';
% 测试集——10个样本
P_test = NIR(temp(51:end),:)';
T_test = octane(temp(51:end),:)';
N = size(P_test,2);
BP神经网络创建、训练及仿真测试
1. 创建网络
net = newff(P_train,T_train,9);
2. 设置训练参数
net.trainParam.epochs = 1000;
net.trainParam.goal = 1e-3;
net.trainParam.lr = 0.01;
3. 训练网络
net = train(net,P_train,T_train);
4. 仿真测试
性能评价
1. 相对误差error
error = abs(T_sim - T_test)./T_test;
2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2));
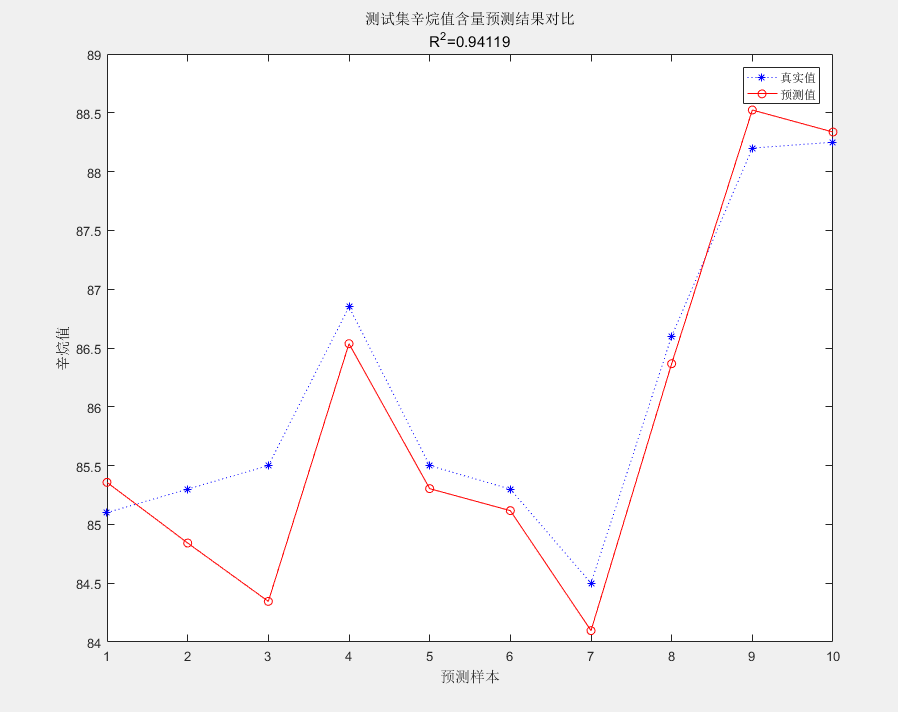
3. 结果对比
result = [T_test' T_sim' error']
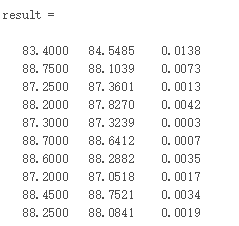
画图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)