匈牙利算法解决二分图最大匹配

预备知识

　　匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是二分图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

二分图

　　二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A，B)，并且图中的每条边（i，j）所关联的两个顶点 i 和 j 分别属于这两个不同的顶点集(i in A，j in B)，则称图G为一个二分图。

匹配

　　在图论中，一个图是一个匹配（或称独立边集）是指这个图之中，任意两条边都没有公共的顶点。这时每个顶点都至多连出一条边，而每一条边都将一对顶点相匹配。

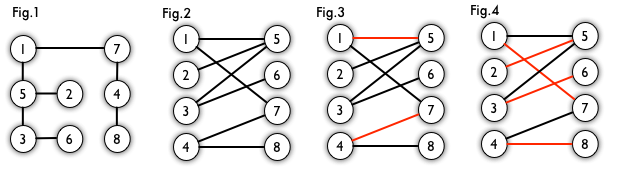
　　例如，图3、图4中红色的边就是图2的匹配。

　　图3中1、4、5、7为匹配点，其他顶点为非匹配点，1-5、4-7为匹配边，其他边为非匹配边。

最大匹配

　　一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

　　任意图中，极大匹配的边数不少于最大匹配的边数的一半。

完美匹配

　　如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。显然，完美匹配一定是最大匹配，但并非每个图都存在完美匹配。

最大匹配数：最大匹配的匹配边的数目。

最小点覆盖数：选取最少的点，使任意一条边至少有一个端点被选择。

最大独立数：选取最多的点，使任意所选两点均不相连。

最小路径覆盖数：对于一个DAG（有向无环图），选取最少条路径，使得每个顶点属于且仅属于一条路径，路径长可以为0（即单个点）

定理1：Konig定理——最大匹配数 = 最小点覆盖数

定理2：最大匹配数 = 最大独立数

定理3：最小路径覆盖数 = 顶点数 - 最大匹配数

 

匈牙利算法

例子

 　　为了便于理解，选取了dalao博客里找妹子的例子：

　　　　https://blog.csdn.net/dark_scope/article/details/8880547

　　 通过数代人的努力，你终于赶上了剩男剩女的大潮，假设你是一位光荣的新世纪媒人，在你的手上有N个剩男，M个剩女，每个人都可能对多名异性有好感（惊讶，-_-||暂时不考虑特殊的性取向）

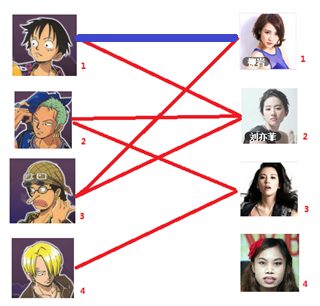
　　如果一对男女互有好感，那么你就可以把这一对撮合在一起，现在让我们无视掉所有的单相思（好忧伤的感觉，快哭了），你拥有的大概就是下面这样一张关系图，每一条连线都表示互有好感。

　　

　　本着救人一命，胜造七级浮屠的原则，你想要尽可能地撮合更多的情侣，匈牙利算法的工作模式会教你这样做：

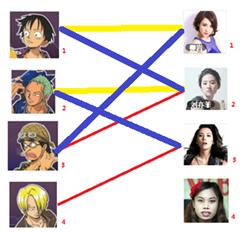
　　一： 先试着给1号男生找妹子，发现第一个和他相连的1号女生还名花无主，got it，连上一条蓝线

　　

　　二：接着给2号男生找妹子，发现第一个和他相连的2号女生名花无主，got it

　　

　　三：接下来是3号男生，很遗憾1号和2号女生已经有主了，怎么办呢？

　　我们试着给之前1号女生匹配的男生（也就是1号男生）另外分配一个妹子。

　　与1号男生相连的第二个女生是2号女生，但是2号女生也有主了，怎么办呢？

　　我们再试着给2号女生的原配(嘤嘤嘤)，重新找个妹子(注意这个步骤和上面是一样的，这是一个递归的过程)

　　此时发现2号男生还能找到3号女生，那么之前的问题迎刃而解了，回溯回去。

　　

　　四：接下来是4号男生，很遗憾，按照第三步的节奏我们没法给4号男生腾出来一个妹子，我们实在是无能为力了……交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。

　　这时，想引入交替路径和增广路径的概念：

　　交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边...形成的路径。

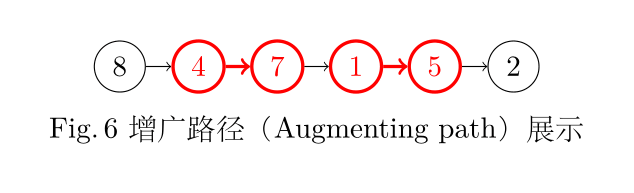
　　增广路：由一个未匹配的顶点开始，经过若干个匹配顶点(走交替路)，最后到达对面集合的一个未匹配顶点的路径，则这条交替路称为增广路（agumenting path）

 　　举例来说，有A、B集合，增广路由A中一个点通向B中一个点，再由B中这个点通向A中一个点……交替进行。

　　

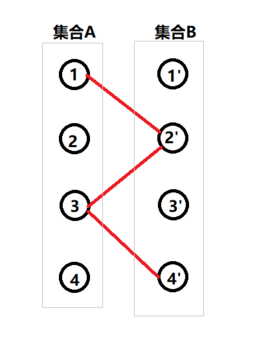
　　增广路径将两个不同集合的两个未匹配顶点通过一系列匹配顶点相连。

　　求最大匹配的一种显而易见的算法是：先找出全部匹配，然后保留匹配数最多的。但是这个算法的时间复杂度为边数的指数级函数。因此，需要寻求一种更加高效的算法。

　　我们可以通过用增广路径求最大匹配，即匈牙利法。

匈牙利法的思想

　　增广路径的首尾是非匹配点。因此，增广路径的第一条和最后一条边，必然是非匹配边；同时它的第二条边和倒数第二条边，必然是匹配边；以及第三条边（如果有）和倒数第三条边（如果有），一定是非匹配边。这样一来，增广路径中非匹配边数 = 匹配边数 + 1。

　　如果我们置换增广路径中的匹配边和非匹配边，由于增广路径的首尾是非匹配点，其余则是匹配点，这样的置换不会影响原匹配中其他的匹配边和匹配点，因而不会破坏匹配，可以得到比原有匹配更大的匹配（具体来说，匹配的边数增加了 1）。

　　

　　由于二分图的最大匹配必然存在（比如，上限是包含所有顶点的完全匹配），所以，再任意匹配的基础上，如果我们有办法不断地搜寻出增广路径，直到最终我们找不到新的增广路径为止，我们就有可能得到二分图的一个最大匹配。这，就是匈牙利法的思想。

　　但是，基于这种贪心的思想，你又如何能证明它是可以找到最大匹配的解？

　　dalao给出以下证明：

　　我们从反证法考虑，即假设存当前匹配不是二分图的最大匹配，但已找不到一条新的增广路径的情况。因为当前匹配不是二分图的最大匹配，那么在两个集合中，分别至少存在一个非匹配点。那么情况分为两种：

　　1. 这两个点之间存在一条边——那么我们找到了一条新的增广路径，产生矛盾；

　　2. 这两个点之间不存在直接的边，即这两个点分别都只与匹配点相连——那么：

　　　　2.1 如果这两个点可以用已有的匹配点相连，那么我们找到了一条新的增广路径，产生矛盾；

　　　　2.2 如果这两个点无法用已有的匹配点相连，那么这两个点也就无法增加匹配中边的数量，也就是我们已经找到了二分图的最大匹配，产生矛盾。

　　在所有可能的情况，上述假设都会产生矛盾。因此假设不成立，亦即贪心算法必然能求得最大匹配的解。

参考地址：https://blog.csdn.net/ctsas/article/details/62421389

 

HDOJ2063

　　我们以HDOJ2063为例。 http://acm.hdu.edu.cn/showproblem.php?pid=2063

过山车

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 33350    Accepted Submission(s): 14266

　　Problem Description

　　RPG girls今天和大家一起去游乐场玩，终于可以坐上梦寐以求的过山车了。可是，过山车的每一排只有两个座位，而且还有条不成文的规矩，就是每个女生必须找个男生做partner和她同坐。但是，每个女孩都有各自的想法，举个例子把，Rabbit只愿意和XHD或PQK做partner，Grass只愿意和linle或LL做partner，PrincessSnow愿意和水域浪子或伪酷儿做partner。考虑到经费问题，boss刘决定只让找到partner的人去坐过山车，其他的人，嘿嘿，就站在下面看着吧。聪明的Acmer，你可以帮忙算算最多有多少对组合可以坐上过山车吗？

 

　　Input

　　输入数据的第一行是三个整数K , M , N，分别表示可能的组合数目，女生的人数，男生的人数。0<K<=1000，1<=N 和M<=500.

　　接下来的K行，每行有两个数，分别表示女生Ai愿意和男生Bj做partner。最后一个0结束输入。

 

　　Output

　　对于每组数据，输出一个整数，表示可以坐上过山车的最多组合数。

 

　　Sample Input

6 3 3

1 1

1 2

1 3

2 1

2 3

3 1

0

　　Sample Output

　　3

 

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f;
using namespace std;
int L[505][505];
int boy[505];
int used[505];
int k,m,n;  //可能的组合数k，女生数m，男生数n 
bool find(int i){
    for(int j=1;j<=n;j++){
        if(L[i][j] && !used[j]){  //跟他有关系而且没有搜索过 
            used[j]=1;
            if(!boy[j] || find(boy[j])){
                boy[j]=i;
                return true;
            }
        }
    }
    return false;
}
int main(){
    while(cin>>k>>m>>n){
        memset(L,0,sizeof(L));
        memset(boy,0,sizeof(boy));
        for(int i=1;i<=k;i++){
            int n1,n2;
            cin>>n1>>n2;
            L[n1][n2]=1;
        }
        int sum=0;
        for(int i=1;i<=m;i++){
            memset(used,0,sizeof(used));
            if(find(i)) sum++;
        }
        cout<<sum<<endl;
    }
    return 0;
}