多目标规划
多目标规划问题特点：
1. 多个优化目标
2. 约束条件有回旋
给出几个实际的例子：
例如要购置一台手提电脑，你想要 1. 内存尽可能大 2. 运行速度尽可能快 3. 重量尽可能轻 4. 体积尽可能小 5. 清晰度要高 6. 性价比要尽可能高 … 这些东西就是目标。
而像：1. 希望价格在5千以内 2. 希望外观比较漂亮 3. 比较坚固 4. 性能要稳定可靠 .....就是一些模糊的约束条件。
又例如，去浙大参加研究生复试，应该怎么走？这就是一个交通工具的选择问题。
每个人都有自己的走法，而 1. 一个小时左右能够到 2. 单程费用不要超过20元 3. 最好车上有坐位 4. 步行路程不要超过1000米 .....之类的约束条件就是很多的目标。
目标形式：
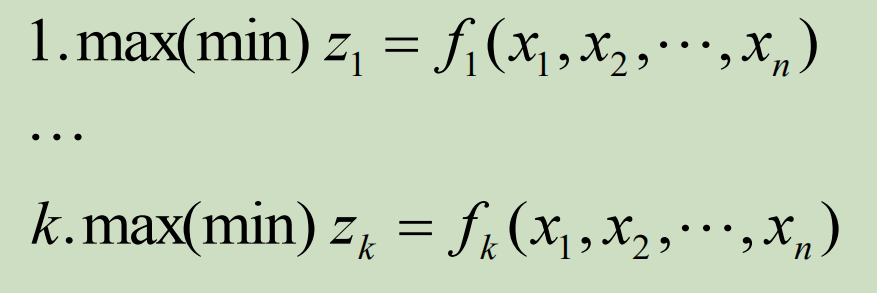
约束形式：
注意：是尽可能满足而不是非要满足！
为了协调多种目标，一般存在两种情况：
1. 同级的多个目标处理
①所有目标函数统一成max形式（或统一成min形式）
②总目标为一个加权求和形
决策者根据实际情况为每个子目标指定权重𝒘𝟏，𝒘𝟐，… ，𝒘𝒌,其中𝒘𝒊/𝒘𝒋为第𝒊个目标关于第𝒋个目标的相对重要性。
那么根据目标形式，得出对应的总目标为：
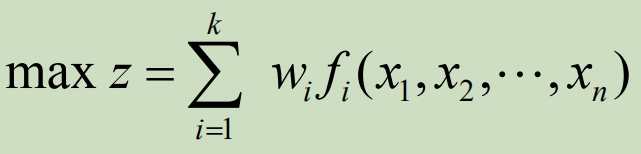
于是我们就可以把多目标规划问题转化为一般的单目标模型：
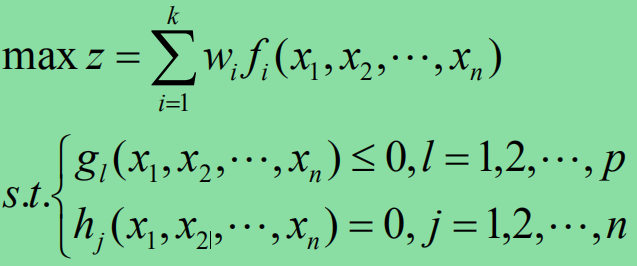
例题：某厂计划在下一个生产周期内生产A，B两种产品，每种产品的单位利润分别为10和18（单位：万元），资源消耗和限制数量如下表，求总利润最大的生产方案。
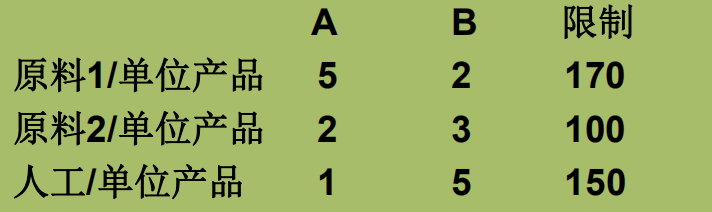
解：设生产A,B,C分别为𝒙𝟏, 𝒙𝟐, 𝒙𝟑个单位，数学模型为：
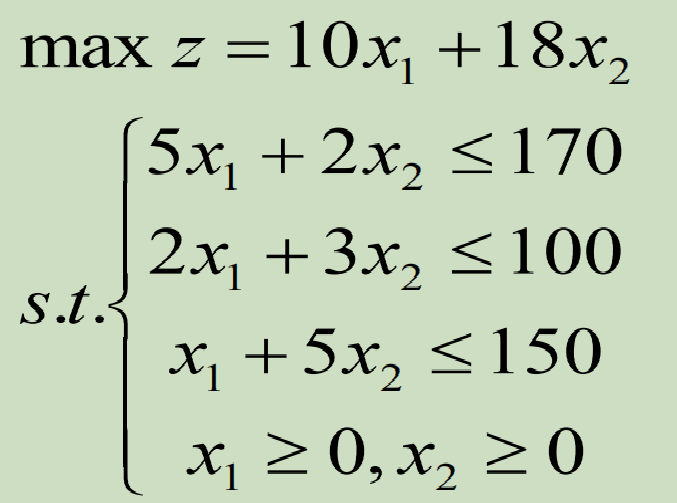
这是一个单目标问题，解得x1=50/7，x2=200/7，最优目标函数值z=4100/7万元。
但是如果考虑到第一种资源面临涨价预期，希望尽可能清空库存利于快速补充，故考虑本期利润最大化的同时必须为下一个周期做好准备，从而增加新目标函数：
，进而就被转化为了一个多目标问题。
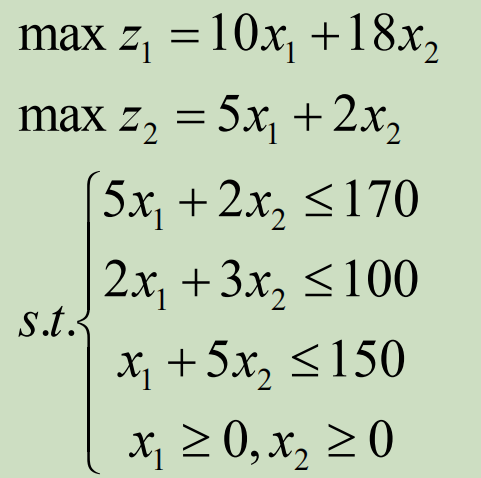
如果目标一比目标二更重要，根据需求设定目标一相比目标二的重要性是2：1，则2个目标可以统一为：
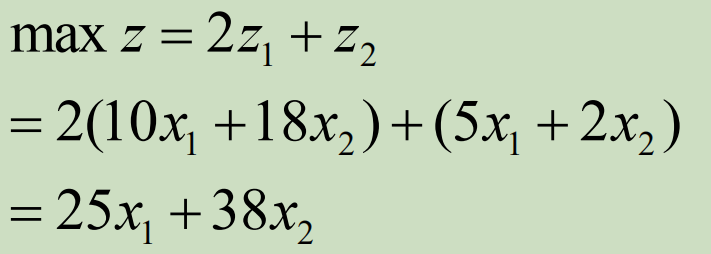
这样，多目标问题就被化为常规的单目标线性规问题了。
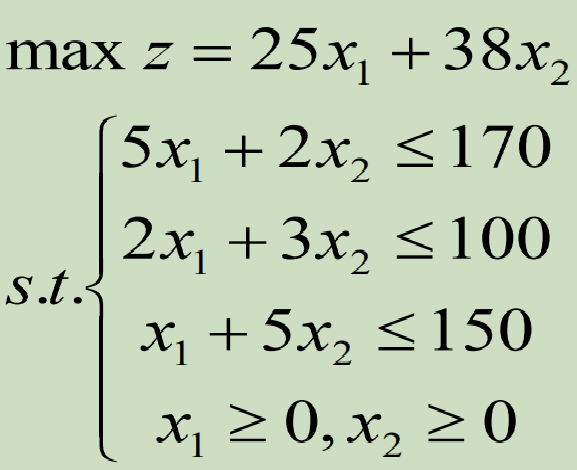
解得x1=550/23，x2=580/23，最优解z≈1556.087。
注意：目标函数的值要无量纲化！
如果𝒛𝟏的变化范围为[minz1,maxz1]，𝒛𝟐的变化范围为[minz2,maxz2]，则原目标可以做如下无量纲化处理：
其他无量纲化处理方法：直线型、折线型、曲线型无量纲方法。
2. 不同级的目标问题
首先要保证目标的主要(𝑷𝟏级)目标，再考虑𝑷𝟐级目标。𝑷𝒊级目标的重要性高于𝑷𝒊+𝟏级的目标的重要性。
绝对约束（也称为系统约束）：必须遵循的约束条件，如产品的产量必须为非负等等。
目标约束：允许带偏差的约束。
常规数学规划模型中的约束是绝对约束。
设 𝒇𝒊（𝒊 = 𝟏, 𝟐, ⋯ ,𝒍 ）为第𝒊个目标函数，它的正偏差变量：，
，表示决策值超过目标值的部分。
负偏差变量：
，表示决策值未达到目标值的部分。这里
表示𝒇𝒊的目标值。
因决策值不可能既超过目标值同时又未达到目标值，即恒有𝒅𝒊+ × 𝒅𝒊− = 𝟎。
例如，希望𝟑𝒙 + 𝟒𝒚大约等于100。
可写成目标约束形式：
如果希望𝟑𝒙 + 𝟒𝒚不超过100，则需要控制正偏差变量，如果希望𝟑𝒙 + 𝟒𝒚至少达到100则需要控制负偏差变量，如果希望𝟑𝒙 + 𝟒𝒚正好等于100，则需要同时控制正负两个偏差变量。
这种用总偏差量最小化形式表示的目标函数称为达成函数（正负偏差的控制通过目标函数来实现）
目标规划形式：
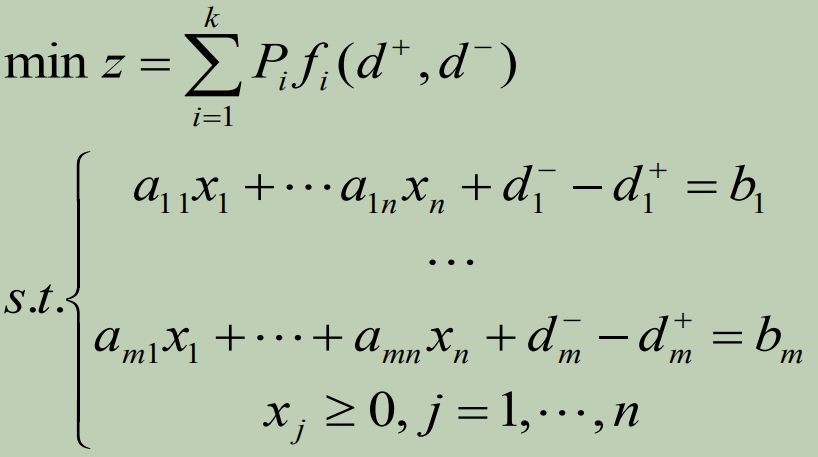
例题：某厂生产A,B, C三种产品,每种产品的单位利润分别为12,18和15（单位万元）,资源消耗和市场需求量如下表：
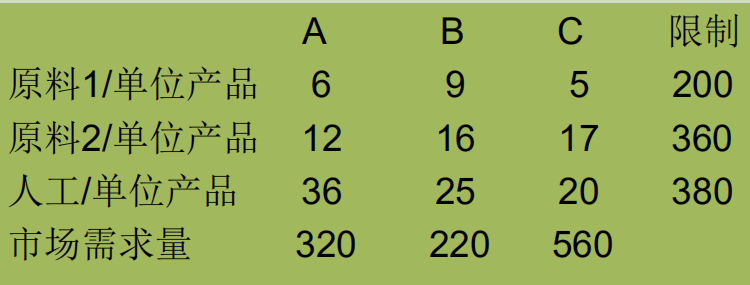
P1级目标： 达到利润指标利润6000万；
P2级目标： 尽量用完第一种资源的库存，不够可以适当外购议价资源；
P3级目标： 尽量不加班，如果需要加班则加班时间不要超过100小时。
达成函数（目标函数）：
设生产A,B,C分别为𝒙𝟏, 𝒙𝟐, 𝒙𝟑个单位，约束条件：
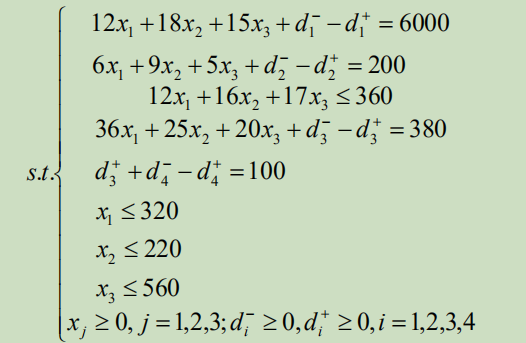
先求解P1级目标问题：
则目标函数为
，并根据最初的约束条件求解。
记求得的最优解为𝒛𝟏 = 𝒄𝟏。
然后将𝒛𝟏 = 𝒄𝟏为约束条件（绝对约束）添加到原目标规划的约束中，求解𝑷𝟐级目标问题：
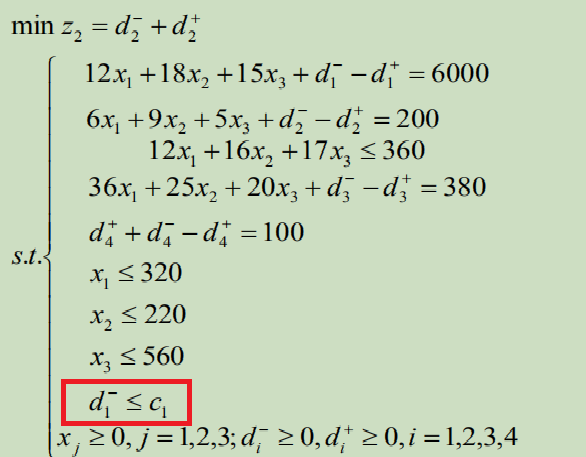
对于解P3级规划问题也是同理。
最后一个单目标规划的规划的求解结果即为目标规划的满意解。
注意：在目标规划中不提最优解的概念，只提满意解的概念（因为不可能所有的目标都达到最优），即寻求能够照顾到各个目标，并使决策者感到满意的解，由决策者来确定选取哪一个解，但满意解的数目太多而难以将其一一求出。
