选址问题
选址问题
设施选址问题(Facility Location Problem)自20世纪60年代初期以来,在运筹学中一直占据着中心位置。它来自于工厂、仓库、超市、学校、医院、图书馆、火车站、代理服务器、传感器等位置的确定问题。
设施选址问题是NP-难解问题,除非P=NP,设施选址问题不存在多项式时间算法。
P问题:
一个问题可以在多项式(O(n^k))的时间复杂度内解决。
NP问题:
一个问题的解可以在多项式的时间内被验证。
NP-hard问题:
任意NP问题都可以在多项式时间内归约为该问题,但该问题本身不一定是NP问题。归约的意思是为了解决问题A,先将问题A归约为另一个问题B,解决问题B同时也间接解决了问题A。
NPC问题:
既是NP问题,也是NP-hard问题。
设施选址问题的近似算法主要分三类:
1. LP rounding
线性规划舍入法:首先给出原问题的线性整数规划模型,然后求解相应的线性规划松弛问题得到分数最优解,根据可行要求对分数最优解进行改造,构造原问题的整数可行解,属于非组合算法。
2. Primal-Dual
原始对偶法:设计组合算法给出对偶问题的可行解,根据该对偶可行解构造原始问题的整数可行解。
3. Local Search
局部搜索法:给定初始可行解,定义适当的邻域,通过引入恰当的调整策略,在邻域中得到改进的可行解,依次迭代,直到调整策略不能改进为止。
1. 选址的意义
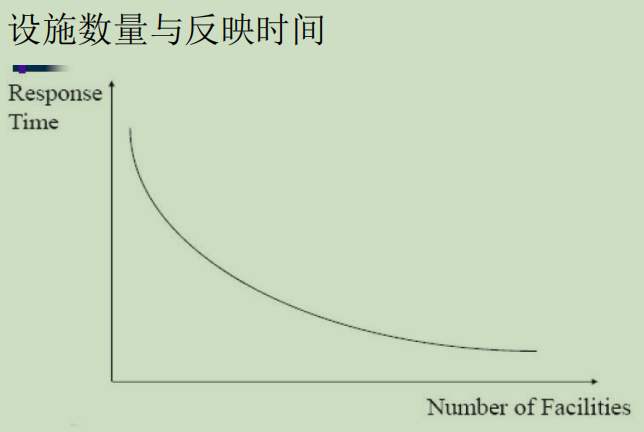
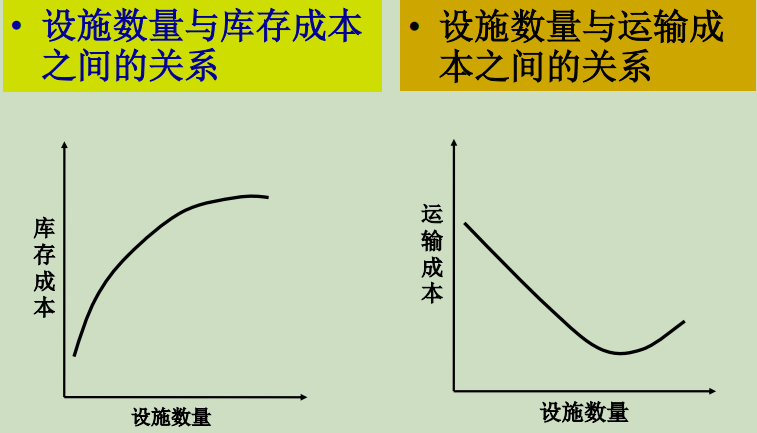
2. 选址问题的程序和步骤
- 选址约束条件分析
- 搜索整理资料
- 地址筛选
- 定量分析
- 结果评价
- 复查和确定选址

选址约束条件分析
(1)需求条件
顾客现在分布,未来分布预测,货物作业量的增长率及物流区域分析。
(2)运输条件
北京市的四道口蔬菜、果品配送中心就建在铁路货运站旁边,并且近靠公路。
(3)配送服务的条件
向顾客报告到会时间、发送频率、根据供货时间计算的从顾客到物流重心的距离和服务范围等。
(4)用地条件
(5)法规
收集整理资料
为正确构造优化模型必须:
(1)掌握业务量
①工厂到物流中心之间的运输量
②向顾客配送的货物数量
③物流中心保管的货物数量
(2)掌握费用
①工厂至配送中心之间的运输量
②物流中心到顾客之间的配送费
③与设施、土地有关的费用及人工费、业务费等
① ②两项费用,随着业务量和运送距离的变化而变动,所以必须对每一吨公里的费用进行分析(成本分析); ③项包括可变费用和固定费用,可以根据可变费用和固定费用之和进行成本分析。
选址问题很重要,但是很困难。(1)选址因素相互矛盾。例如:利于配送的地方能较多地接受业务,但常常地价贵、租金高。(2)不同因素的相对重要性很难确定和度量。(3)判断的标准会随着时间的变化而变化,现在认为好的选址,过几年就不一定是好的选址。
家乐福的选址 -对物流中心选址的启发
家乐福1995年进入中国市场后,短时间内在相距甚远的京、上海和深圳三地开了大卖场,这是因为可以对立地发展出自己的供应网络。
根据家乐福自己的统计,从中国本地购买的商品占了商场里所有商品的95%以上,仅2000年采购金额就达15亿美元。除了已有的上海、广东、浙江、福建及胶东半岛等各地的采购网络,家乐福还在北京、天津、大连、青岛、武汉、宁波、厦门、广州及深圳开设区域采购网络。
家乐福(Carrefour)的法文意思是“十字路口”,而家乐福的选址也不折不扣地体现这一标准--几乎所有的都开在十字路口。店址的选择,其背后精密和复杂的计算,将令行业外人士大吃一惊。
第一,测算商圈内的人口消费能力。中国早期没有现成的资料可以利用,所以店家不得不借助市场调研公司的力量来收集这方面的信息。
有一种做法是以某个原点出发,测算5分钟步行会到什么地方,然后是10分钟步行会到什么地方,最后是15分钟会到什么地方。根据中国的本地特色,还需要测算以自行车出发的小片、中片和大片半径,最后是以车行速度来测算小片、中片和大片各覆盖了什么区域。如果有自然分隔线,如一条铁路线,或是另一个街区有一个竞争对手,商圈的覆盖就需要依据这种边界进行调整。然后,需要对这些区域进行进一步的细化,计算这片区域内各个居住小区的数量和密度、年龄分布、文化水平、职业分布、人均可支配收入等许多指标。家乐福的做法更细致一些,它根据这些小区的远近程度和居民可支配收入,又划定了重要销售区和普通销售区域。
第二,研究这片区域内的城市交通和周边商圈的竞争情况。如果一个未来的店址周围有许多的公交车,或是道路宽阔,交通方便,那么销售辐射的半径就大为放大。上海的大卖场都非常聪明,例如家乐福古北点周围的公交线不多,家乐福干脆自己租用公交车定点在一些固定的小区间穿行,方便这些离得比较远的小区居民上门一次性购齐一周的生活用品。当然,未来潜在销售区域会受到很多竞争对手的挤压,所以家乐福也将未来所有的竞争对手计算进去。传统的商圈分析中,需要计算所有竞争对手的销售情况,产品线组成和单位面积销售额等,然后将这些顾及估计的数字从总的区域潜力中减去,未来的销售潜力就产生了。另外,家乐福还对它的顾客进行了详细分析:顾客中有60%在34岁以下,70%是女性,然后有28%的人走路,45%乘坐公共汽车而来。所以,大卖场可以依据这些目标顾客的信息来微调自己的商品线。
3. 选址问题的早期研究
早期的选址工作总是以运输成本为基础的。尽管大多数研究是在农业和早期工业社会条件下进行的,他们所提出的许多概念一直沿用至今。
-
地租出价曲线(Bid-Rent Curves)
从宏观方面可以将选址方法分成两类:
(1)运输成本最小化方法
(2)利润水平最大化方法
运输成本最小化方法是由德国农业学家杜能(Johann von Thünen)在1875年就农产品的仓库选址问题提出的。
Johann von Thünen的选址模型有两个假定条件:
✓ 假定1:农产品的销售价格和生产成本在各个不同的市场上都是相同的。
✓ 假定2:由于农民的利润为农产品的销售价格减去其生产成本和运输成本,因而最优的选址策略应当是使运输成本最小。
杜能( Johann von Thünen )认为,任何经济开发活动能够支付给土地的最高地租或利润是产品在市场内的价格与产品运输到市场的成本之差。如今,当我们观察围绕城市中心环形分布的零售、居住、生产制造和农业区时,会发现这一观点仍然适用。那些能够支付最高地租的经济活动将分布在距离城市中心最近的地区以及主要运输枢纽的周边地带。

-
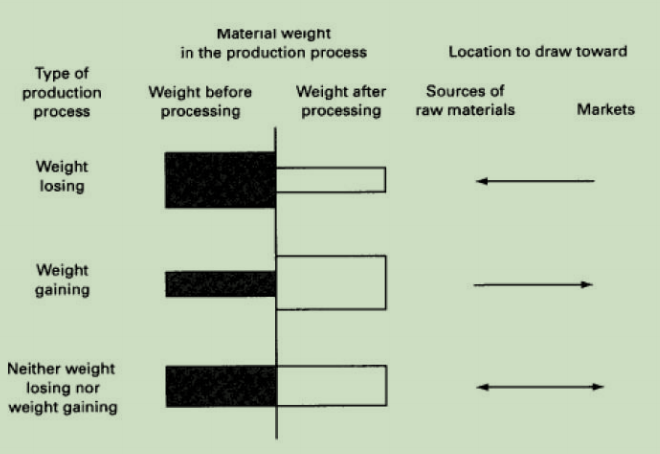
韦伯(Weber)的工业分类
韦伯(Weber)在1909年提出:对于使重量减少的生产过程(产成品重量小于原材料的重量),最好工厂建在距原材料处近些。对重量增加的生产过程,最好将工厂建在距市场近的地方以减少运输费用。对于没有重量损失的原材料选址可建立在任何合适的地方。
(1)钢铁厂炼钢——最好工厂建在距原材料处近些
(2)饮料厂装罐——工厂建在距市场近的地方。
(3)装配线生产——成品重量是装配过程中使用的所有零部件重量之和。
Weber's Classification of Industries
-
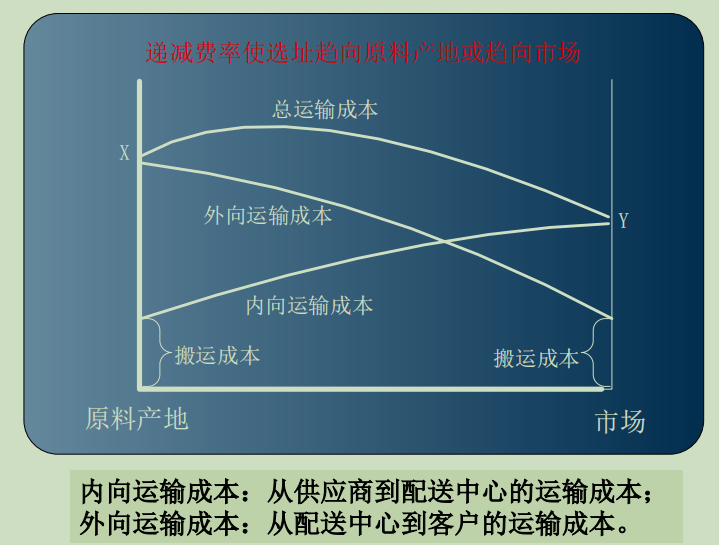
胡佛(E.M. Hoover)的递减运输费率
胡佛观察到:运输费率随着距离的增加,增幅下降。如果运输成本是选址的主要决定因素,要使内向运输与外向运输的总成本最小,位于原料产地和市场之间的设施必然可以在这两点之中找到运输成本最小的点。
4. Minisum/Minimax目标函数
- 中心点—经济平衡性
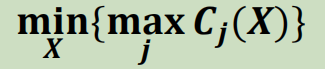
- 中心点(中值)—经济效益性
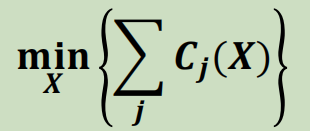
- 反中心(Anti-Center)
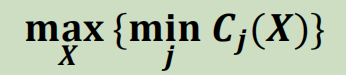
假设在一条直线上,在为宗旨0、5、6、7上有四个点,每个点服务的成本与这些点和新设施间的距离成正比。

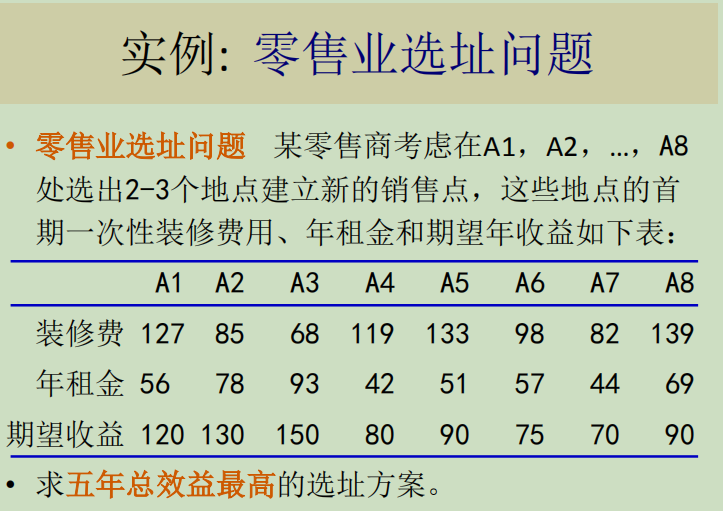
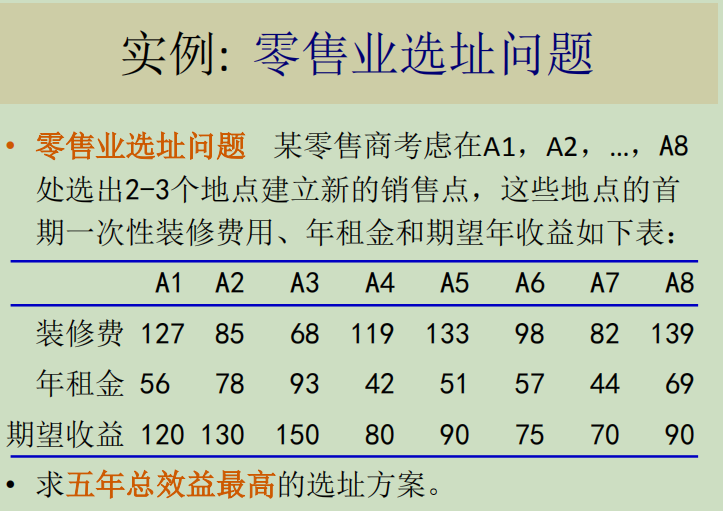
上述模型是一个整数线性规划问题,可以用LINGO软件求解.
- 但实际生活中,收益往往是一个随机变量,它带有明显的不确定因素。如果只是满足于求解上面这种形式的数学模型,只不过求解了一个数学应用题。
- 数学模型应该考虑更多的实际因素:如果根据抽样调查数据,我们发现年收益可以设为分布已知的随机变量
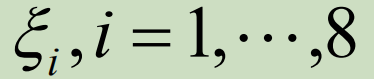 。
。
则数学模型为:
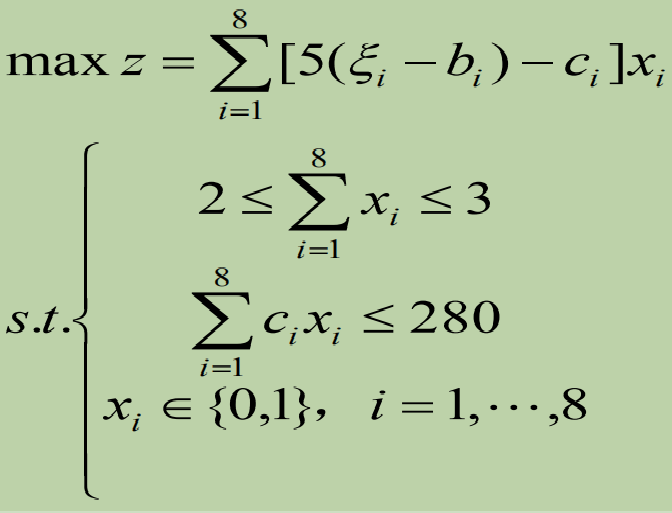
注意到𝒙𝒊是决策变量,可以由投资者自行决定,以求得更高的回报,但𝝃𝒊却不受决策者控制,它们是性质完全不同的随机变量。
上面的数学模型称为随机规划模型。随机规划的求解可以从不同角度出发,得到不同的答案。
收益保障模型



- 很少有参赛队主动分析最坏情况。
- 想到控制风险的不少,但做出实质性风险控制决策的很少。
- 注意数学建模竞赛要争取做得比多数人好,才能胜出。要考虑实际问题中一些应该做的数据分析,比如效益波动范围,可靠性(把握)分析(灵敏度分析)等等。
- 不能只是有问有答,不问不答。
- 从不同角度出发得到的数学模型和问题的答案往往是不同的。
- 事实上,有人选择高回报的投资,有人选择稳健型的。高回报往往伴随高风险,回避风险也往往得不到高收益。“撑死胆大的,饿死胆小的。”
- 选定一种方案后,要能够对模型进行较为全面的分析。比如我们选择了期望值模型,求解出结果后,应该对目标函数的实际变化区间做一个估计,对有可能出现的最坏情况进行分析。
5. 0-1整数规划方法选址

如图,新建一个物流中心,有𝒔个候选地点,分别为𝑫𝟏, 𝑫𝟐, ⋯ , 𝑫𝒔 ;原材料、燃料、零配件的供应地有𝒎 个,分别用 𝑨𝟏,𝑨𝟐, ⋯ , 𝑨𝒎 表示,其供应量分别为𝑷𝟏,𝑷𝟐, ⋯ ,𝑷𝒎表示;产品销售地有𝒏个,分别为𝑩𝟏, 𝑩𝟐, ⋯ , 𝑩𝒏 表示,其销量分别用𝑸𝟏, 𝑸𝟐, ⋯ , 𝑸𝒏表示。
从𝒔个候选地点中选取一个最佳地址建物流中心,使物流费用达到最低。记𝑪𝒊𝒋表示从𝑨𝒊到𝑫𝒋的每单位量的运输成本;𝒅𝒊𝒋表示从𝑫𝒋到𝑩𝒌的每单位量的运输成本;𝑷𝒊𝒋表示从𝑨𝒊到𝑫𝒋的运量,𝑸𝒋𝒌表示𝑫𝒋到𝑩𝒌的运量。引进变量𝑿 = 𝑿𝟏,𝑿𝟐, ⋯ ,𝑿𝒔,其中 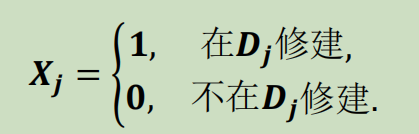
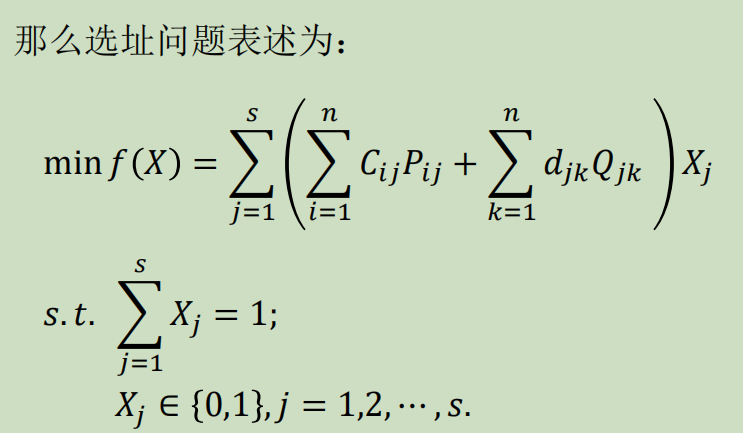
- 引入0-1变量的实际问题
某公司拟在北京的东、西、南三区建立物流配送中心,拟议中有7个位置𝑨𝒊(𝒊 = 𝟏, 𝟐, ⋯ , 𝟕)可供选择。作如下规定:
◼在东区,由𝑨𝟏, 𝑨𝟐,𝑨𝟑 中至多选2个;
◼在西区,由𝑨𝟒, 𝑨𝟓 中至少选1个;
◼在南区,由𝑨𝟔, 𝑨𝟕 中至少选1个。
如选用𝑨𝒊点,设备投资估计为𝒃𝒊元,每年可获利润估计为𝒄𝒊 元,但投资总额不能超过𝑩元。问应选择哪几个点可使年利润最大?

6. 单设施选址
一般的单设施选址模型
给出现有设施位置、新设施和现有设施之间的运输量,确定使总运输费用最的最优选址方案。(运输费用是以运输距离乘以运输量来确定的)
直角选址模型(折线距离)

欧几里德选址模型(精确重心法)

优点:此类方法不限于在特定的备选地点进行选择,灵活性较大。
缺点:①由于自由度较大,由迭代计算求得的最佳地点实际上往往很难得到。因为,所选地址可能位于河流、湖泊中间或街道中间,还有的地点可能在自然条件不容许选用的地方等。
②另外,从所选设施地点(如物流中心)向需求点发送,被认为都是直线往复的运输,这也是不符合实际的。实际上,多数情况是一辆车巡回于数个零售店之间,而且通常要考虑实际的道路距离,这就使这种方法的求解相当复杂。这也是这种方法的另一缺点。
加权因素分析
这种方法既可考虑影响设施选址的定量因素也可考虑定性因素,但在分析之前需要确定一系列候选地点。
步骤流程:
①确定选择地点时需考虑的因素及标准、各评 价标准的权重或相对重要性。
②给每个地点的所有因素从1到10进行打分。
③

影响地点选择的主要因素
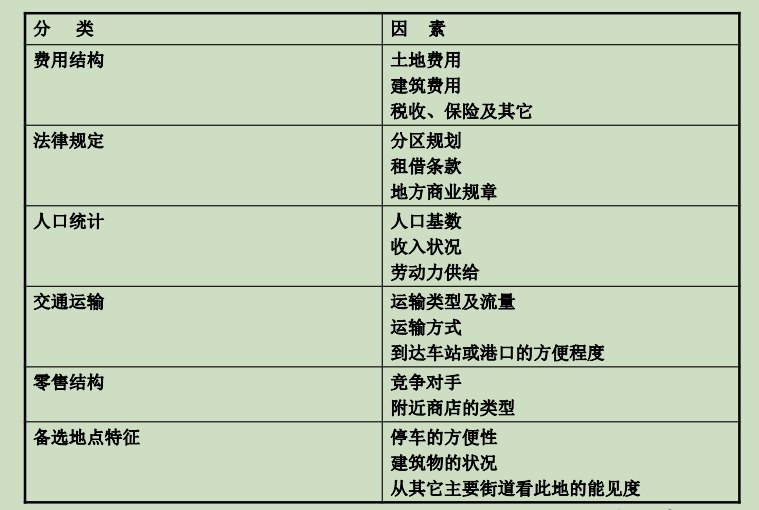
单设施选址模型的推广
精确重心法的连续选址特性和其简单性使其不论是作为一个选址模型,还是作为更复杂方法的子模型都很受欢迎,也鼓舞着研究者拓展模型的功效。
精确重心模型有许多推广模型,其中主要有:考虑客户服务和收入,解决多设施选址问题,引入非线性运输成本等。
对单设施选址问题的评述
没有任何模型具有某一选址问题所希求的所有特点,也不可能由模型的解能够直接导出最终决策,或者说管理人员只需把选址问题委托给分析人员就高枕无忧了。因此,我们只能希望这些模型可以提供指导性解决方案。有效利用这些模型不仅需要我们充分认识其优势,还需要了解其缺陷。
这些单设施选址模型的优点是他们有助于寻找选址问题的最优解,而且因为这些模型能够充分真实地体现实际问题。
模型的缺点:选址模型的结果有可能失实。但主要看问题的敏感程度。
7. 多设施选址
对大多企业而言,其面临的问题往往是必须同时决定两个或多个设施的选址,虽然问题更加复杂,却更接近实际情况。多设施选址问题很普遍,因为除了非常小的公司以外,几乎所有公司的物流系统中都有一个以上的仓库。由于不能将这些仓库看成是经济上相互独立的,而且可能的选址布局方案相当多,因而问题十分复杂。
精确法
含义:精确法是指这样一些方法,这些方法能够保证得到选址问题的数学最优解,或者至少是精确度已知条件下的解。
优势:精确法在许多方面堪称解决选址问题的理想方法。微积分和数学规划模型即属于该类方法。
劣势:该方法将导致计算机运行时间很长,要求的内存空间巨大,且在适用于实际问题时会有一些问题定义不太准确。
多重心法
精确重心法是一种以微积分为基础的模型,用来找出起讫点之间使运输成本最小的中介设施的位置。
如果要确定的点不止一个,就有必要将起讫点预先分配给位置待定的设施。这就形成了个数等于待选址设施数量的许多起讫点群落。
随后找出每个起讫点群落的精确重心点。针对设施进行起讫点分配的方法很多,尤其是在考虑多个设施及问题涉及众多起讫点时。方法之一是把相互间距离最近的点组合起来成群落,找出各群落的重心位置,然后将各点重新分配到这些位置已知的设施,找出修正后的各群落新的重心位置,继续上述过程直到不再有任何变化。这样完成了特定数量设施选址的计算。该方法也可以针对不同数量的设施重复计算。
如果能够评估所有分配起讫点群落的方式,那么该方法是最优的。尽管如此,就实际问题的规模而言,在计算上却是不现实的。即便预先将大量顾客分配给很少的几个设施,也是一件极其庞杂的工作。因此还需要使用其他方式。
模拟法
针对实际选址问题得到的最优解不好或不可行,可以采用模拟的方法进行评判。
在模拟方法中,问题的复杂性及各种变量之间的相关关系用一些公式进行建模,模型的输入用概率分布进行描述,然后运行模拟模型来模仿实际系统的运行状态及其随时间变化的过程,并通过对模拟运行过程的观察和统计得到被模拟系统的输出参数和基本特性,以此估计和推断实际系统的真实参数和性能。
模拟模型与算术选址模型不同,它要求分析员或管理人员必须明确网络中需要的特定设施。根据被挑选出来等待评估的个别设施及其分配方案判断这是最优的,还是接近最优的选址方式。
8. 动态设施选址
在有些情况下,选址决策是动态的。
原因:由于从某一阶段到下一阶段对现有设施的需求不同、新设施能力不同或新设施的运行费用不同而造成的。在动态情况下,必须对新设施重新选址来满足变化了的费用结构及其它需求。
出现的问题:将会导致花费过大,这些费用包括在旧址上关闭设施的费用,搬移设备和从旧址到新址搬运零件的费用及在新址初始的采购和安装费用。在有些情况下,由于契约及条款等其它原因不能重新选址。
解决办法:最好的方法就是把未来时段的需求和能力数据综合考虑,将未来的费用转为现值,再用单阶段模型求解当前阶段的最佳位置。解决问题时会出现的两种情况:
(1)当可以重新选址及其费用可以忽略时,那么对每一个阶段单独求解问题就可以了。
(2)当重新选址费用过高时,这个问题求解时应考虑每个阶段的选址费用和一个阶段到另一个阶段重新选址费。
9. 零售/服务设施选址
包括内容:零售和服务中心常常是实物分销网络中的最后储存点,这里包括百货商店、超级市场、分支银行、紧急救护中心、教堂、废品回收中心、消防队和警察局。
特点:对这些点的选址分析通常会对收入、可达性等因素高度敏感,而不像工厂和仓库选址那样更重视成本因素。
是否接近竞争对手、人口构成、顾客交通模式、是否靠近互补性商店、是否方便停车、是否接近好的运输线路、社区对服务的接受程度等因素仅仅是影响零售/服务选址众多因素中的一小部分。因此,前面介绍的方法无法直接应用到这些问题。



