整数规划模型
问题中许多量具有不可分割的性质(最优调度的车辆数、设置的销售网点数......),或者问题的解必须满足一些特殊的约束条件(满足逻辑条件、顺序......),需引入逻辑变量(0-1变量)以表示“是”与“非”。这类问题的模型均为整数规划模型。
纯整数规划模型:仅由整数变量组成的模型
混合整数规划模型:普通的连续变量和整数变量同时出现的模型
如果把整数规划问题中变量的整数约束松弛为任意实数的约束,则对应的线性规划问题成为原问题的松弛问题。
求解整数规划问题比求解线性规划问题困难,至今尚无统一的有效算法。
分支定界法(Branch and Bound,简称B&B)
操作步骤有以下三步:
如图可行域为OABCDE,设最优解在C处,此时Xr不是整数,我们就考虑从可行域中划分出不相交的两部分(Sub1和Sub2),除去的部分要求包含最优解C而且不包含任何整数解的区域。
这样用原来的目标函数,构造两个子问题Sub1和Sub2。
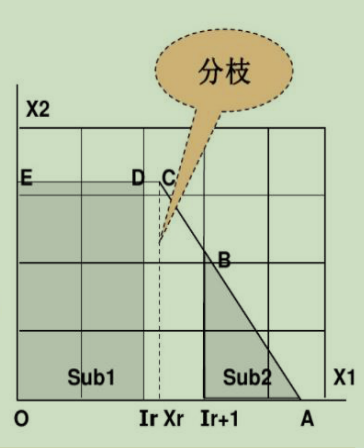
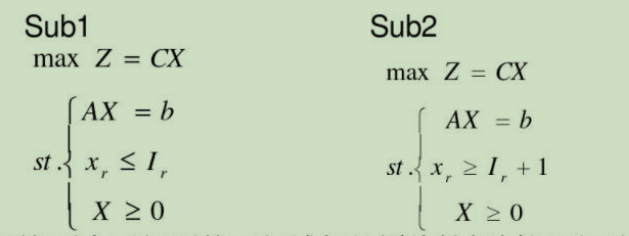
1. 分支
由于这两个子问题的可行域都是原线性规划问题的子集,这两个子问题的最优解的目标函数值都不会比原线性规划问题的最优解的目标函数值大。
如果这两个问题的最优解仍不是整数解,则继续选择一个非整数的变量,继续讲这个子问题分解为两个更下一级的子问题。这个过程被称为“分支”。
2. 定界
3. 比较和剪枝
每一次分支得到的子问题最优解的目标函数值,都小于或等于分之前的最优解的目标函数值。非整数解的最大值作为新的上界。
如果某一个子问题的最优解是整数解,就作为整数规划最优目标函数值的下界,多个子问题存在整数解时,取最大值。最后的下界为整数规划的最优解。
如果某一个子问题的解还不是整数解,但这个非整数解的目标函数值已经小于这个下界,那么这个子问题就不必再进行分支。
确定整数解的目标函数值上下界不断更新,“剪除”目标函数值小于下界的分支的过程,称为定界。
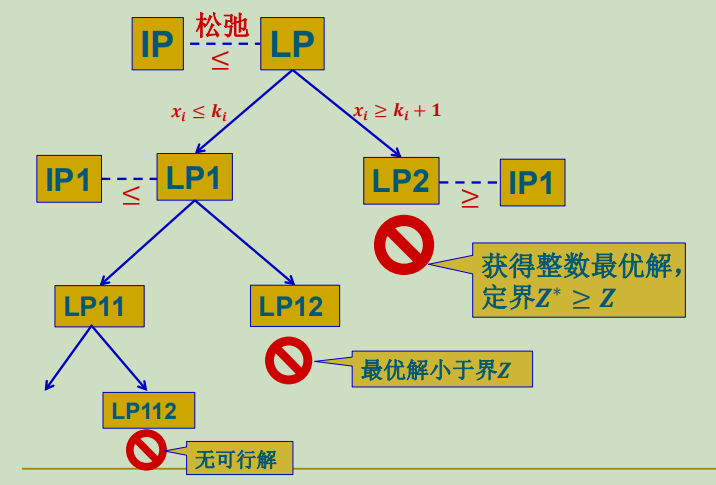
例如:
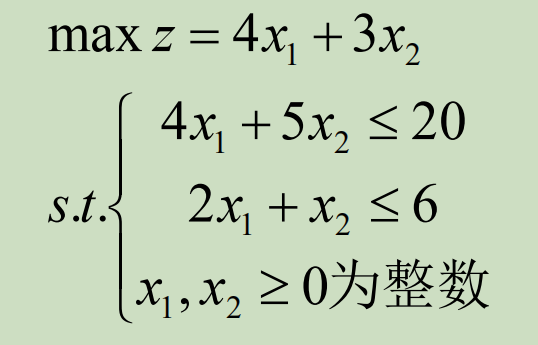
解得X=(5/3 , 8/3)^T , Z = 44/3
我们就可以把它分成X1≤1和X2≥2两个分支。
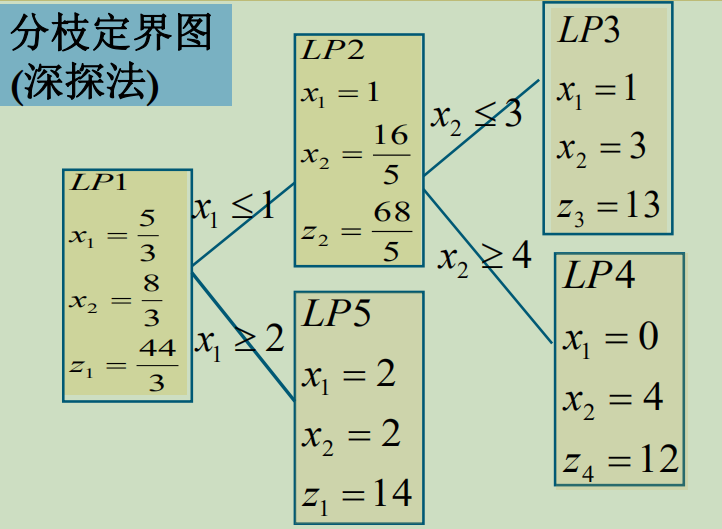
1. 深探法
对LP2进行深探,LP2不满足整数解条件,对LP2的分支LP3和LP4进行深探,发现是满足的。
在对LP1的另一个分支LP5深探。LP5满足整数解条件,比较目标函数值之后,LP5的解是最优解。
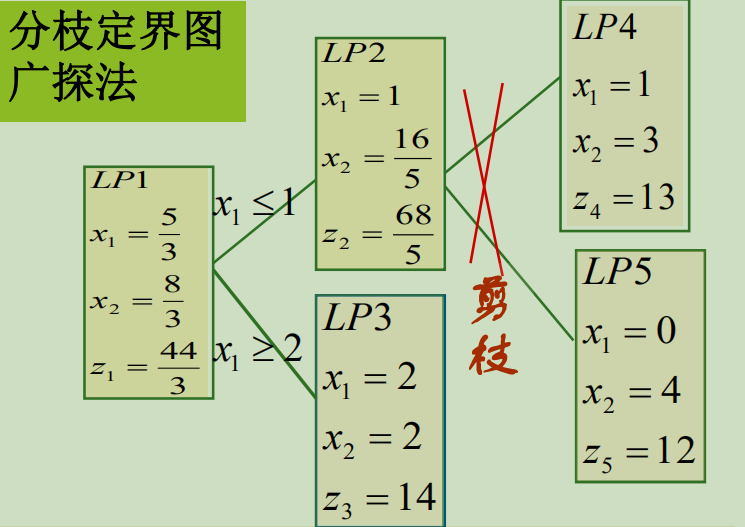
2. 广探法
由于LP1的分支LP2不符合整数解要求,而另一分支LP3符合,进行剪枝即可,没有必要对LP2分支。
3. 混探法
(先广探,再找一枝看似有希望的分支进行深探)
图的遍历算法中,有两个基本搜索算法:
-
深度优先搜索DFS(深探法)
-
广度优先搜索BFS(广探法)
DFS算法计算所需内存较小,搜索到最优解计算次数的期望值较大。
BFS搜索到最优解计算次数的期望值较小,但所需内存空间很大。
不管是深探法、广探法、还是混探法都不能避免最优解在搜遍所有节点后才确定的情况。但是一个好的分支定界搜索算法可以在平均意义下提高算法的搜索效率。
指派问题与匈牙利法

指派问题模型为一个0-1规划模型。
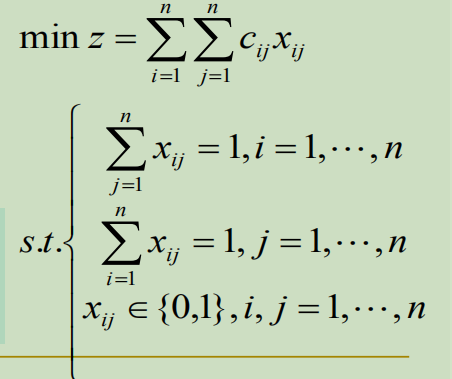
标准的指派问题是一类特殊的整数规划问题,又是特殊的0-1规划问题和特殊的运输问题。匈牙利解法的关键是利用了指派问题最优解的性质:若从指派问题系数矩阵的某行(或某列)各元素分别减去一个常数k,得到新的矩阵与原矩阵有相同的最优解。
对于指派问题,由于系数矩阵均为非负,故若能载系数矩阵中找到n个不同行和不同列的0元素(独立的0元素),则对应的指派方案总费用为0,从而一定是最优的。
例题:
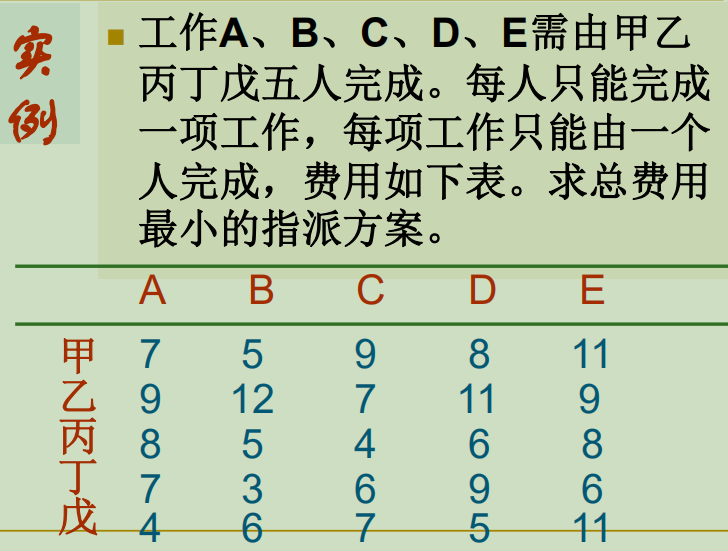
1. 减去最小数
费用矩阵每行减去该行的最小数,使最小数变0
费用矩阵每列减去该列的最小数,使最小数变0
即:先对行操作,
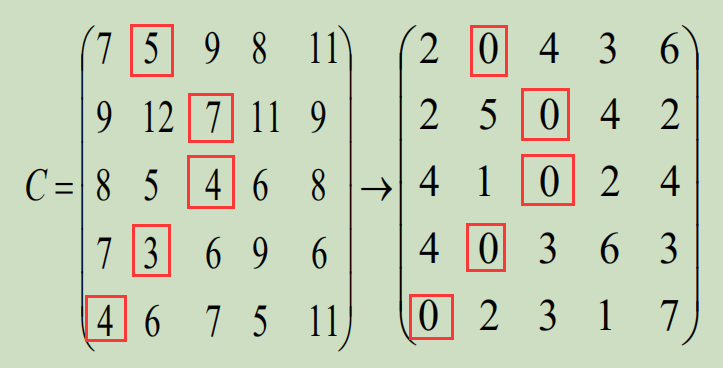
再对列操作,
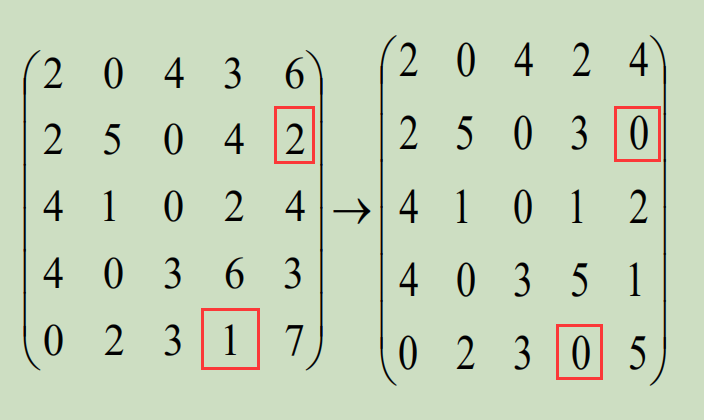
2. 试分配
先找0最少的行,给0画圈,划去与圈同行以及同列的0
再找0最少的列,给0画圈,划去与圈同行以及同列的0
不断进行以上这组操作,直到所有的0被圈掉或划掉。
就得到:
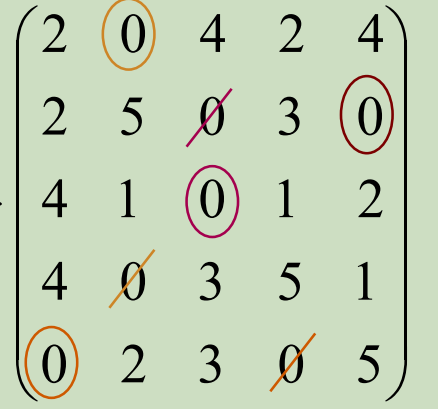
- 无O行打√
- 新打√行找0,对有0列打√
- 新打√列找O,对有O行打√
反复2和3,直到打不出√。最后,对无√行划横线,有√列划竖线,构成覆盖零的最少直线
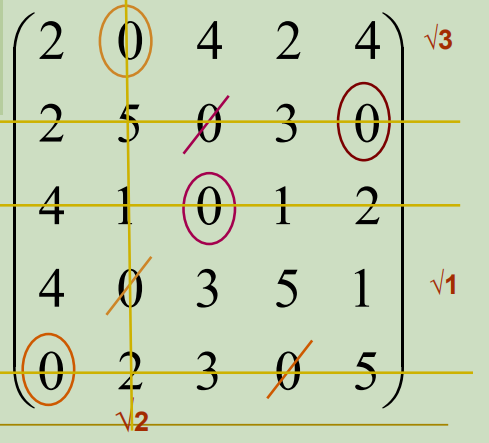
3. 匈牙利法:找覆盖0的最少直线(直线数与圈数相符)
令𝜽 为未覆盖数中最小者(此例中𝜽是1)
1. 未覆盖数 统一减去𝜽
2. 单线覆盖数保持不变
3. 双线覆盖数统一加上𝜽
(打√ 行减𝜽 ,打√ 列加𝜽 )
得到:
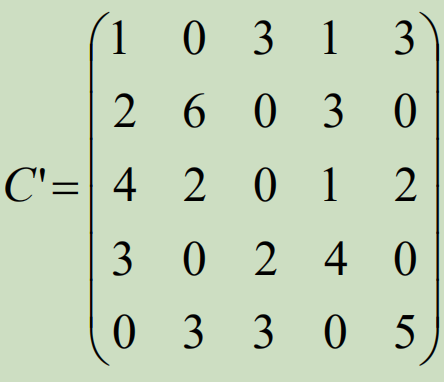
对这个新的费用矩阵用圈0划0,使用匈牙利法.
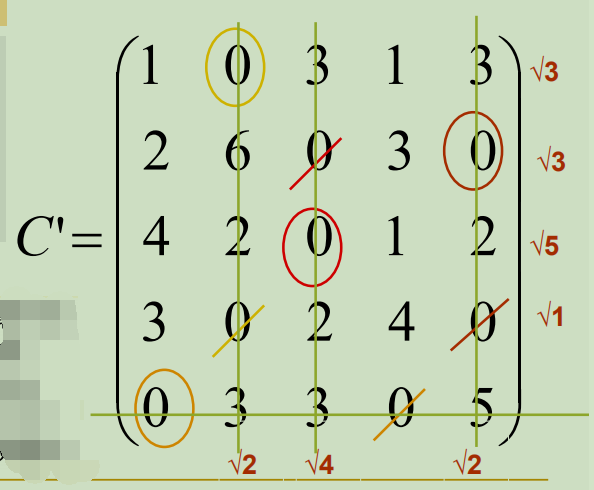
得到:
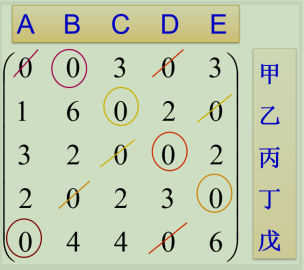
于是,可以安排:甲——B;乙——C;丙——D;丁——E;戊——A
总费用最小为:5+7+6+6=28。


