线性规划对偶问题
生产计划优化
企业的生产计划优化问题就是一类对偶问题。
例如:某厂生产A,B, C三种产品,每种产品的单位利润分别为12,18和15,资源消耗如下表,求总利润最大的生产方案。
| A | B | C | 限制 | |
| 原料1/单位产品 | 6 | 9 | 5 | 200 |
| 原料2/单位产品 | 12 | 16 | 17 | 360 |
| 人工/单位产品 | 25 | 20 | 12 | 780 |
设生产A,B,C分别为𝒙𝟏, 𝒙𝟐, 𝒙𝟑个单位,数学模型为(LP):
\[\begin{array}{l}
\max z = 12{x_1} + 18{x_2} + 5{x_3}\\
s.t.\left\{ {\begin{array}{*{20}{c}}
{6{x_1} + 9{x_2} + 5{x_3} \le 200}\\
{12{x_1} + 16{x_2} + 17{x_3} \le 360}\\
{25{x_1} + 20{x_2} + 12{x_3} \le 780}\\
{{x_1} \ge 0,{x_2} \ge 0,{x_3} \ge 0}
\end{array}} \right.
\end{array}\]
考虑到资源限制:
如果把接受外来加工任务看成将企业的三种资源(原料1、原料2和人工)出售给对方,每单位资源$i$售价(利润)为$y_i$,$i$ = 1、2、3,则6个单位资源1加12个单位资源2再加上25个小时人工相当于一个单位产品A,故这些资源的总售价应至少为产品A的售价,不然给别人加工不如自己生产产品A。
即 6$y_1$ + 12$y_2$ + 25$y_3$ ≥ 12。
同理有9$y_1$ + 16$y_2$ + 20$y_3$ ≥ 18。
5$y_1$ + 17$y_2$ + 12$y_3$ ≥ 15。
我们得到如下对偶线性规划(DLP):
\[\begin{array}{l}
\min z = 200{y_1} + 360{y_2} + 780{y_3}\\
s.t.\left\{ {\begin{array}{*{20}{c}}
{6{y_1} + 12{y_2} + 25{y_3} \ge 12}\\
{9{y_1} + 16{y_2} + 20{y_3} \ge 18}\\
{5{y_1} + 17{y_2} + 12{y_3} \ge 15}\\
{{y_1} \ge 0,{y_2} \ge 0,{y_3} \ge 0}
\end{array}} \right.
\end{array}\]
- 线性规划及其对偶互为对偶规划。
- 当一对对偶线性规划问题都有可行解时,对偶问题的最优目标值与原始问题的最优目标值相等。
线性规划对偶
对称型:
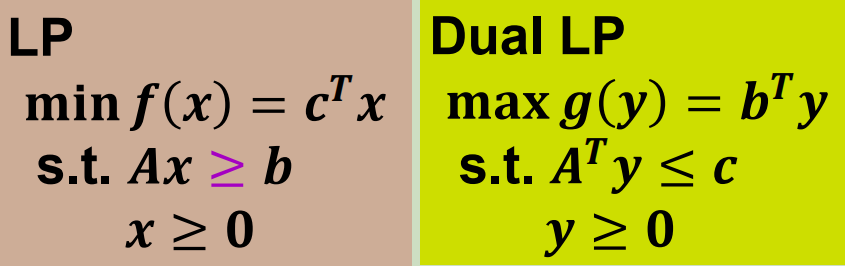
上面的那两组就属于对称型。
而对于标准型,也可以给出几个例子:
①

②

对偶问题解的实际意义:
- 了解本企业资源价格𝑦1, … , 𝑦𝑚(称为影子价格);依据市场价格𝑝𝑖与企业资源价格𝑦𝑖的差异,若 𝑦𝑖 − 𝑝𝑖 > 0 ,则从市场购进资源 𝑖 ,经过调整产量,可以获得更大的利润。
- 企业合作谈判中可以知己知彼,不吃亏的同时也不失去机会


