单纯形法
在求解LP问题时,有人给出了图解法,但对多维变量时,却无能为力。
于是,美国数学家G.B. Dantzig (丹捷格)发明了一种“单纯形法”的代数算法,尤其是方便于计算机运算。这是运筹学史上最辉煌的阶段。
翻译一下就是:
-
若某个基本可行解对应的检验向量<0,那么这个基本可行解就是最优的。
-
若某个基本可行解对应的检验向量=0,则有无穷多个最优解。
-
若某个基本可行解对应的检验向量>0,并且系数(约束条件)小于0,无解。
${C_N}$——非基变量系数
${C_B}$——基变量系数
B——基,即线性无关向量组R(A)=R(B)
N——非基向量组
单纯形法计算步骤:
-
将线性规划问题化成标准型 (引入松弛变量)
-
找出或构造一个m阶单位矩阵作为初始可行基,建立初始单纯形表。
-
计算各非基变量的检验数${\sigma _j} = {c_j} - {z_j}$ 若所有检验数≤0,则问题已得到最优解,停止计算。否则,转入下一步。(检验数)
-
在大于0的检验数中,若某个检验数对应的系数列向量≤ 0,则此问题是无界解,停止计算,否则转入下步。
-
根据$max$(检验数$j$ | 检验数$j$>0)=检验数k的原则,确定为换入变量(进基变量) 再按最小比值法则($\frac{{{b_i}}}{{{a_{ik}}}}$,&${a_{ik}}$>0)确定换出变量,建立新的单纯形表,此时的基变量中${x_k}$代替的换出变量的位置。
-
以${a_{ik}}$为主元素进行迭代,把${x_k}$所对应的列向量变为单位列向量,即${a_{ik}}$变为1 同列中其他元素变为0,继续计算各非基变量的检验数,进行第三步。
&Lingo里面的方法就属于单纯形法。

例题:

①先引入三个松弛变量,构造单位矩阵。

②得到单位矩阵,构造出初始可行基B

从中我们可以get信息:基向量组B和非基向量组N
还可以知道所有变量的系数所组成的向量C和基变量${X_B}$、非基变量${X_N}$:
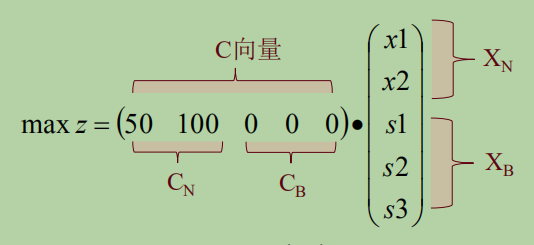
我们需要的检验数就是系数减去${Z_j}$(${\sigma _j} = {c_j} - {z_j}$,${Z_j} = {C_B}{N_j}$)
这是目标函数:$Z = {C_B}{B^{ - 1}}b + ({C_N} - {C_B}{B^{ - 1}}N){X_N}$ (b就是增广矩阵多出来的那些)
当基矩阵B化成单位矩阵时,令非基变量${X_N}$=0,得到 $Z = {C_B}{B^{ - 1}}b$
③进行步骤3--6

填入信息
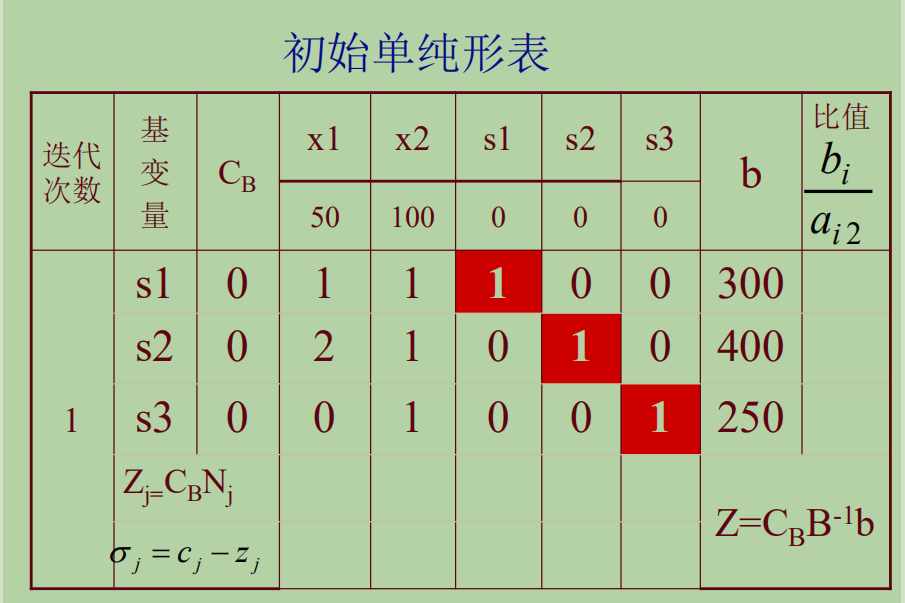
刚开始,基变量的系数全为0,所以Z=0,${Z_j}$=0,可以写出对应的检验数:
|
x1 |
x2 | s1 | s2 | s3 |
| 50 | 100 | 0 | 0 | 0 |
可以看出,${x_2}$对应的检验数最大,成为换入变量,而且根据最小值法则,知道${s_3}$是换出变量。于是将${s_3}$的位置换上${x_2}$,对应的系数也变成了100。

我们再进行初等行变换,使${x_2}$,${s_1}$,${s_2}$对应的基矩阵变成单位矩阵。在此基础上进行计算${Z_j}$,就可以利用其算出新一轮的检验数:
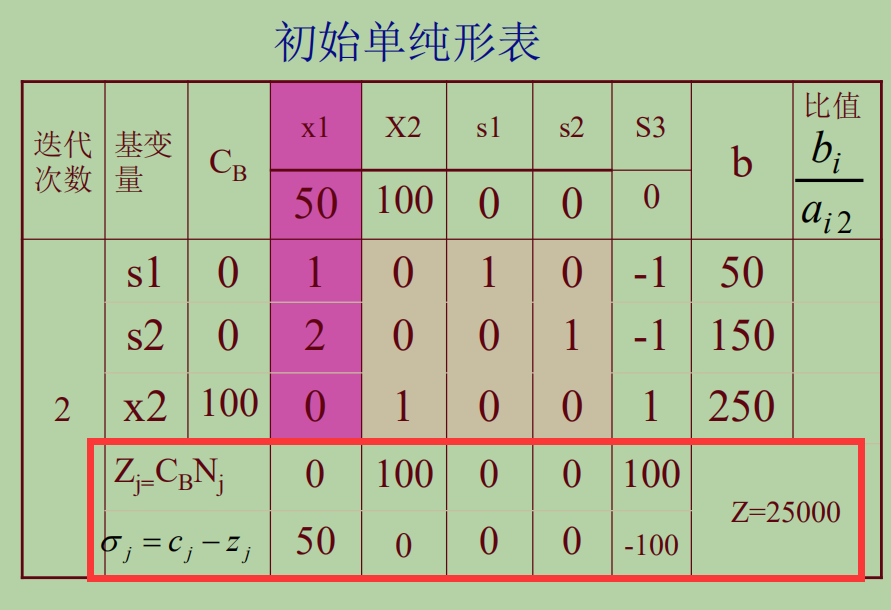
我们可以发现,仍然存在检验数大于0的情况,唉,只能进入新一轮的迭代,${x_1}$作为换入变量,而经过最小比值规则,可以判定出${s_1}$是换出变量

然后,我们再根据新的数据,写出新一轮的${Z_j}$和 检验数 ,发现此时的检验数全部≤0,我们成功地找到了最优解!

结束啦!
表格中,检验数全部≤0,根据判断规则,Z值为最优值(Z=27500),其解:
${X_1}$=50,${s_1}$=50,${X_2}$=250,${s_2}$=${s_3}$=0
为模型的最优解。



