数学规划及其应用
数学规划是优化问题建模的第一步,也是最为重要的一步,它界定了问题的类型和求解难度。
正确建立优化问题的数学规划模型,必须做到充分理解问题本身。
此外,应该
- 选择最佳的决策变量。
- 确定合适的目标函数(可能不止一个)。
- 根据问题的要求写出所有的约束条件。
建立数学规划后,还需判定其类型。
最后,利用软件或设计算法求解数学规划。
一般线性规划的特点是约束条件可以用一组线性不等式或线性等式表示,目标函数为决策变量的线性函数,根据问题的不同,要求目标函数实现最大化或最小化。
满足以上条件的数学模型成为线性规划问题的数学模型。
一般标准形式为:

c称为价值向量、A称为约束矩阵、x称为决策变量向量,b称为右端向量
那么,如何将线性规划问题转化为标准形式?

数学规划的分类
LP(线性规划)、ILP(整数线性规划)、0-1整数规划是三种典型的数学规划。
MILP(混合整数规划):目标或约束均为线性函数、决策变量既有整数又有非整数的数学规划。
NLP(非线性规划):目标函数或约束条件中含有非线性函数的数学规划。
其中,决策变量取整数的非线性规划称为非线性整数规划。
二次规划,属于非线性规划,但目标函数多为二次多项式函数,约束条件为线性多项式。
注:
整数规划的计算复杂度(计算机计算工作量)远远超过同规模的线性规划。
线性目标、非线性约束模型通常比非线性目标函数、线性约束模型更难计算
建模时应尽可能将目标、约束写成线性形式。
例如:
- 假设0-1决策变量𝑧𝑖𝑗 = 1时,要求决策变量 𝑥𝑖 ≥ 𝑦𝑗
- 写法一: 𝑥𝑖 ≥ 𝑦𝑗 𝑧𝑖𝑗 非线性
- 写法二: 𝑥𝑖 ≥ 𝑦𝑗 − 𝑀(1 − 𝑧𝑖𝑗),其中𝑀为充分大的整数。 线性
厨师任务分配问题

某饭店共有两名厨师,可制作20道菜,其中制作第𝒊道菜所需时间为𝒕𝒊 。某天来了5桌客人,到店时间和下单情况见附表。
要求:
每桌的A-E菜必须先上;
M菜须等半小时以后方可制作;
如果同时点了R和S、或者R和T菜,则最后赠送一份F菜。
问:
1、怎样分配厨师任务,使得两名厨师尽可能同时下班?
2、怎样分配厨师任务,使得5桌客人的平均等菜时间尽可能短?
注:由于客人对菜品口味要求不同,每道菜原则上不允许同时制作两份。
送货问题

送货问题—线性规划—运输问题模型
运输问题可以分为三种问题模型:
-
产销平衡模型
-
销大于产模型
-
产大于销模型
设批发点𝐴𝑖运往零售店𝐵𝑗的运量为𝒙𝒊𝒋。
产销平衡时,![]() 各个批发点的库存总和正好满足所有零售店的需求,送货问题的数学模型为:
各个批发点的库存总和正好满足所有零售店的需求,送货问题的数学模型为:
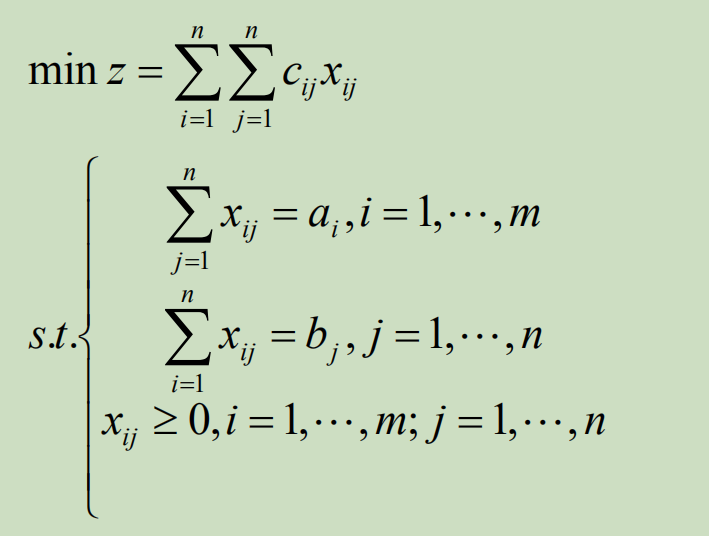
销大于产时,![]() ,各个销地的需求不一定能够得到满足,运输问题的数学模型为:
,各个销地的需求不一定能够得到满足,运输问题的数学模型为:
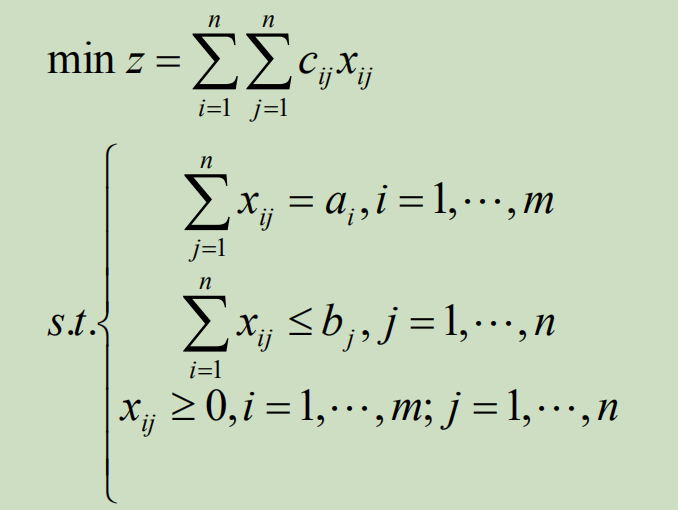
产大于销时,![]() ,各个销地的需求一定能够得到满足,但各个产地的物资不一定全部运走。运输问题的数学模型为:
,各个销地的需求一定能够得到满足,但各个产地的物资不一定全部运走。运输问题的数学模型为:

产销平衡运输问题一定存在最优解。
线性规划
约束为等号形式
bi≥0,i=1,2.......m
xj≥0,j=1,2........n
引入松弛变量——把不等号转换成等号。
基本解:非基变量全部等于0的解。
基本可行解:同时满足X≥0的基本解。
基本可行解与可行域的顶点是一一对应的 。(即线性规划的最优解一定是在顶点上)
二、 优化软件
优化软件是求解优化模型的最常用的工具和检验自编算法性能好坏的比较和参照标准。如MATLAB、Lingo
数学建模的两个重要过程:
-
将实际问题抽象成一个数学模型
-
模型求解
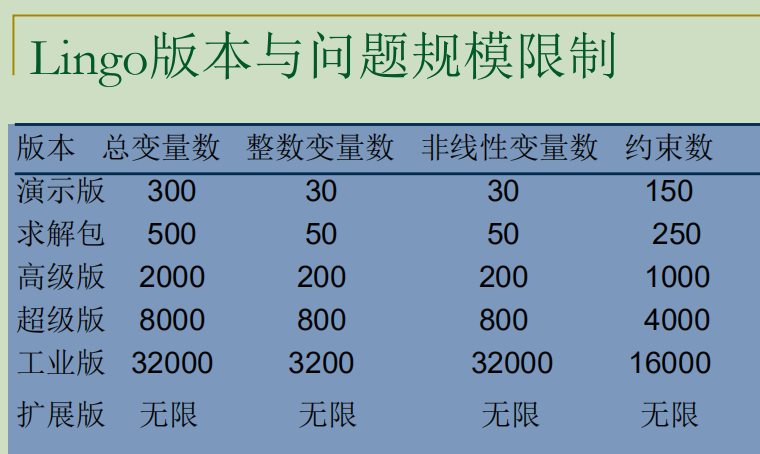
Lingo的约束越多,规模越大,装演示版基本就够了。
韩中庚运筹学投资问题
某公司拟制定今后5年的投资计划,初步考虑以下四个投资项目:
◼ 项目A:从第1年到第4年每年年初需要投资,于次年年末收回成本,并可获利15%;
◼ 项目B:第3年末需要投资,到第5年末可收回成本,预期获利25%,但为了保证足够的流动资金,规定该项目投资金额上限不超过总资金的40%;
◼ 项目C:第2年年初需要投资,到第5年年末可收回成本,预期获利40%,该项目投资金额不能超过总投资额的30%;
◼ 项目D:5年内每年年初可以购买公债,于当年末归还本金,获利6%。该公司现有投资金额100万元,试制定5年总收益最大的投资计划。
设 𝒙𝒊𝒋分别为第𝒊年年初投入到第𝒋 个项目(A、B、C、D)的投资额,则数学模型为:

&:当变量个数很多时,可以尽量使用简单的描述形式,比如用 ∑
Lingo/Lindo与Matlab程序的比较:
Lingo/Lindo程序更接近普通模型。(输出更适合做灵敏度分析,而且Lingo的格式更加灵活,适合处理优化模型)
Matlab程序标准型的要求限制更多一点。(Matlab输出数据不包含灵敏度分析)
社会实际问题数据库—中国统计年鉴
优化问题数学规划形式
连续型问题模型
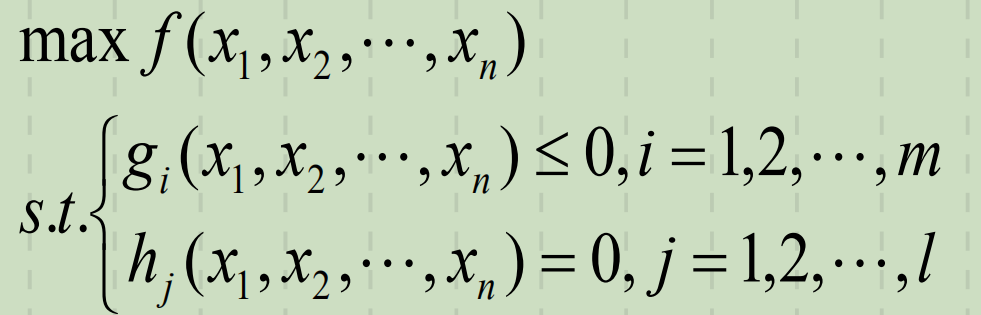
离散型问题模型

判断准确是计算合理的前提,要注意计算方法的准确性和先进性
优化模型的分类
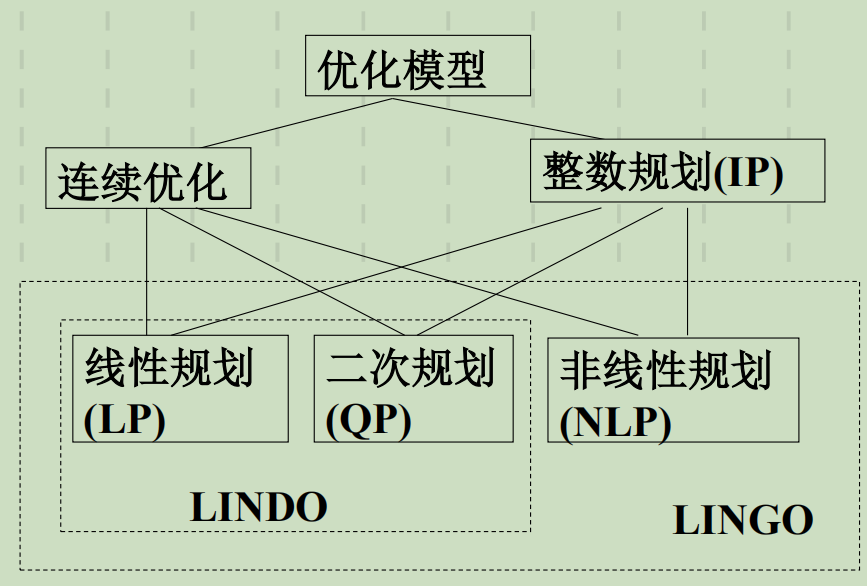
Lingo/Lindo软件的求解过程



