软件分析笔记:2.数据流分析
1数据流分析基础
1.1停机问题-抽象方法
针对基础篇中的停机问题,我们可以试用抽象方法去尝试解决问题。邪恶程序存在的关键在于程序中有if存在 。因此可以采取以下方式。
1.1.1忽略掉所有程序的if条件部分
void Evil(){
if(!Halt(Evil))return;
else while(1)
}
抽象成
void Evil(){
向左走return;
向右走while(1);
}
语义:“向左走/向右走”为非确定性选择,程序随机从“向左走” 和“向右走”后面的语句中选择一条执行。
1.1.2忽略所有条件判断中的条件,一律抽象为不确定选择
void Evil(){
再来一次
向左走goto再来一次;
向右走return;
}
1.1.3抽象过程分析
针对给定输入
- 原始程序只有一条执行路径,抽象程序上有多条执行路径
- 原始程序的执行路径一定包含在抽象程序的执行路径中
停机问题
- 原始程序停机:存在自然数n,程序的执行路径长度 小于n
- 抽象程序停机:存在自然数n,程序中所有执行路径 的长度都小于n
1.1.4停机问题的判定方法
绘制控制流图(结点为程序语句,边为语句间的转移 ), 如果控制流图上有环,则可能不终止,否则一定终止。
1.2符号分析
1.2.1分析内容
给定一个只包含浮点数变量和常量的程序,已知输入的符号,求输出的符号。
1.2.2符号分析的抽象
抽象符号
- 正 =
- 零=
- 负=
- 槑=
1.2.3符号分析的基本思路
给定程序的一条执行路径,我们能推出结果符号的抽象取值。
给定程序的两条执行路径,我们得到两个结果符号的抽象取值 𝑣1,𝑣2,我们可以用如下的操作来合并这两个值:


如果我们能知道程序所有可能的路径产生的结果 符号𝑣1,𝑣2,…,我们就知道了程序的最终结果⊓ (𝑣1,𝑣2,… )。
如何知道程序有哪些可能的路径?
- 近似方案1:忽略掉程序的条件判断,认为所有分支 都有可能到达 .
如何能遍历所有可能的路径?
- 近似方案2:不在路径末尾做合并,在控制流汇合的 所有位置提前做合并
1.3数据流分析单调框架
目标:通过配置框架的参数,可以导出各种类型 的算法,并保证算法的安全性、终止性、收敛性。
1.3.1名词解释
半格(semilattice)
半格是一个二元组(S,⊓),其中S是一个集合,⊓ 是一个交汇运算,并且任意𝑥,𝑦,𝑧 ∈ 𝑆都满足下 列条件:
- 幂等性idempotence: 𝑥 ⊓ 𝑥 = 𝑥
- 交换性commutativity: 𝑥 ⊓ 𝑦 = 𝑦 ⊓ 𝑥
- 结合性associativity: 𝑥 ⊓ 𝑦 ⊓ 𝑧 = 𝑥 ⊓ (𝑦 ⊓ 𝑧)
- 存在一个最大元⊤,使得𝑥 ⊓ ⊤ = 𝑥
偏序Partial Order
偏序是一个二元组(S, ⊑),其中S是一个集合, ⊑ 是一个定义在S上的二元关系,并且满足如下性质:
- 自反性:∀𝑎 ∈ 𝑆:𝑎 ⊑ 𝑎
- 传递性:∀𝑥,𝑦,𝑧 ∈ 𝑆:𝑥 ⊑ 𝑦 ∧ 𝑦 ⊑ 𝑧 ⇒ 𝑥 ⊑ 𝑧
- 非对称性:𝑥 ⊑ 𝑦 ∧ 𝑦 ⊑ 𝑥 ⇒ 𝑥 = 𝑦
每个半格都定义了一个偏序关系
- 𝑥 ⊑ 𝑦当且仅当𝑥 ⊓ 𝑦 = 𝑥
1.3.2半格示例
抽象符号域的五个元素和交汇操作组成了一个半格,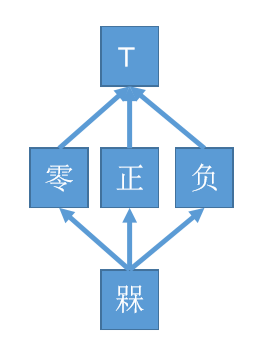
半格的笛卡尔乘积(𝑆 × 𝑇,⊓𝑥𝑦)还是半格
任意集合和交集操作组成了一个半格
- 偏序关系为子集关系
- 顶元素为全集
任意集合和并集操作组成了一个半格
- 偏序关系为超集关系
- 顶元素为空集
半格和偏序关系
每个半格都定义了同一集合SSS上的一个偏序关系
例如,正整数集合上的"求最小公倍数运算"是半格,而"整除关系"是对应的偏序。
又如,任意集合和"交集操作"组成了一个半格,顶元素是全集,而"子集关系"是对应的偏序。
又如,任意集合和"并集操作"组成了一个半格,顶元素是空集,而"超集关系"是对应的偏序。
半格的高度
定义: 半格的偏序图中任意两个结点 的最大距离+1。
1.3.3单调(递增)函数 Monotone (Increasing) Function
定义:给定一个偏序关系(𝑆,⊑),称一个定义在𝑆上的 函数𝑓为单调函数,当且仅当对任意𝑎,𝑏 ∈ 𝑆满足
- 𝑎 ⊑ 𝑏 ⇒ 𝑓 (𝑎) ⊑ 𝑓 (𝑏)
- 注意:单调不等于a ⊑ 𝑓 (𝑎)
单调函数示例
- 在符号分析的半格中,固定任一输入参数,抽象符号 的四个操作均为单调函数
- 在集合和交/并操作构成的半格中,给定任意两个集 合GEN, KILL,函数𝑓 (𝑆) =( 𝑆 − 𝐾𝐼𝐿𝐿) ∪ GEN为单调函 数
1.3.4数据流分析单调框架
- 一个控制流图(𝑉,𝐸)
- 一个有限高度的半格(𝑆,⊓)
- 一个entry的初值𝐼
- 一组结点转换函数,对任意𝑣 ∈ 𝑉 − 𝑒𝑛𝑡𝑟𝑦存在 一个结点转换函数𝑓v
算法伪代码:
2.数据流分析应用
2.1Reaching Definitions可达定值分析
2.1.1原理
如下图所示,我们在p点定义了一个变量v,在p到q的路径中,如果v被重新定义了,那么我们就说这个变量被“杀死了”,如果变量没有被杀死,那么v的值就可以顺利传导到q点。可达定值分析常常用来判断某个已经被声明的变量是否被使用过。

2.1.2分析过程
我们继续使用Abstract和safe-approximation两步骤来进行可达定值分析。
-
Abstraction:将所定义的每个变量状态用bit vectors来表示,如下图所示:
![]()
-
Safe-approximation:我们假设有一个声明D: v = x op y,这条语句新增了一个对于v的声明,并杀死了所有其他对于v的声明,语句的其他部分不受影响。转换函数如下:
![]()
一个简单的实例如下所示:
![]()
每个基本块诞生和杀死的声明如上图所示,这个很好理解。
2.1.3可达定值分析的伪代码

我们先将所有BB的输出设置成空,然后利用我们的转换函数对于每一个BB的输入输出进行迭代,在一次迭代过程中如果有BB的输出发生变化则进行下一次迭代,直到所有BB的输出都不变为止。
may analysis一般都初始化为空,must analysis一般都初始化为Top
2.1.4可达定值分析实例
如下图所示是一个可达分析的实例,可以自己试着按照上面的伪代码做一下分析,看最终的结果是什么。

最终结果是:


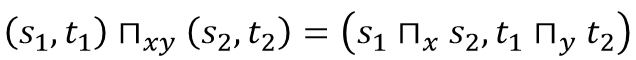




 浙公网安备 33010602011771号
浙公网安备 33010602011771号