计数杂题

搞一点计数题放在这，看到有意思的计数就更（虽然在组合数学那已经更了好多了）。

[CTSC2017] 吉夫特

给定一个长度为 \(n\) 的序列 \(a\)，保证 \(a_i\) 互不相同。求出有多少个长度大于等于二的序列满足

\[\prod _{i=2}^{k} \binom{a_{b_{i-1}}}{a_{b_i}} \bmod 2 = \binom{a_{b_1}}{a_{b_2}} \times \binom{a_{b_2}}{a_{b_3}} \times \cdots \binom{a_{b_{k-1}}}{a_{b_k}} \bmod 2 > 0 \]

方案数对 \(10^9+7\) 取模。

数据范围：\(n\le 211985, a_i\le 233333\)。

---

我们考虑这个序列的性质，即这些组合数中不能出现偶数。我们考虑如何利用这个性质。

我们把组合数的计算公式搬出来：\(\dbinom{n}{m}=\frac{n!}{m!(n-m)!}\)，为了让它为奇数，我们需要让上下阶乘的 \(2\) 的个数相等。

我们考虑把阶乘分解，设 \(f(x)\) 为 \(x!\) 所含的 \(2\) 的个数，则易得：

\[f(x)=\sum_{i=1}^{+\infty} \frac{x}{2^i} \]

我们再设 \(g(x)=x\)，\(h(x)\) 为 \(x\) 二进制中 \(1\) 的个数，则

\[\begin{aligned} g(x)&=g(\frac{x}{2})+\frac{x}{2}+(x\bmod 2)\\ &=\sum _{i=1}^{+\infty} \frac{x}{2^i}+h(x) \\ &=f(x)+h(x) \end{aligned} \]

则 \(f(x)=g(x)-h(x)=x-h(x)\)。再根据需要让上下阶乘 \(2\) 的个数相等，能得出来 \(h(n)=h(m)+h(n-m)\)，即 \(n\) 二进制下 \(1\) 的个数等于 \(m\) 二进制下 \(1\) 的个数加 \(n-m\) 二进制下 \(1\) 的个数。我们考虑如何满足这个条件。

考虑 \(n=(\cdots 00100\cdots)_2, m=(\cdots 00010\cdots)_2\)，那么 \(n-m=(\cdots 00010\cdots)_2\)。显然不可能 \(1\) 的个数相等，因此我们必须满足 \(m\) 是 \(n\) 的子集。

这样就好做了。我们先把所有数存一下位置，从后往前扫，枚举 \(a_i\) 的子集，看是否在 \(i\) 后面，转移即可。

时间复杂度：\(O(\mathrm{能过} )\)。

[HNOI2012] 集合选数

给定一个集合 \(\{1, 2, 3\cdots n \}\)，问有多少满足下述限制的子集：如果 \(x\) 在该集合中，那么 \(2x, 3x\) 不能在该集合中。

数据范围：\(n\le 10^5\)。

---

很有意思的一道题。

我们考虑从一个数为左上角开始构造出一个矩阵，这个矩阵每个数都是它左边数的 \(2\) 倍，是它上面的数的 \(3\) 倍。比如以 \(1\) 为例，构建出的矩阵即为：

\[\begin{bmatrix} 1& 2& 4& 8& \cdots&\\ 3& 6& 12& 24& \cdots&\\ 9& 18& 36& \cdots &\cdots&\\ 27& \cdots& \cdots& \cdots& \cdots&\\ \cdots &\cdots &\cdots &\cdots &\cdots \end{bmatrix} \]

这样，我们就把问题转化为了：在这个矩阵中选择数字，满足选择的数字不相邻。同时我们发现，每个矩阵的方案互不干扰。我们就可以每个矩阵求一遍。

不难看出，这个矩阵的大小最多为 \(\log_2 n\times \log_3 n\)。我们可以直接状压 dp，是一个比较经典的状压 dp 问题。可以直接用插头 dp 解决。

时间复杂度：\(O(\mathrm{能过})\)。

Piling Up

一开始有 \(n\) 个颜色为黑白的球，但不知道黑白色分别有多少。\(m\) 次操作，每次先拿出一个球，再放入黑白球各一个，再拿出一个球，最后拿出的球按顺序排列会形成一个颜色序列，求颜色序列有多少种。

数据范围：\(1 \le n \le 3000,1 \le m \le 3000\)

---

很容易设计出状态 \(f[i, j]\) 为 \(i\) 次操作后有 \(j\) 个黑球时的方案数，也很容易写出状态转移：

\[f[i, j]=f[i-1, j-1]+f[i-1, j+1]+f[i-1,j]+f[i-1,j] \]

即四种拿出球的顺序：黑黑、白白、黑白、白黑。答案即为 \(\sum f[m][i]\)。

但是我们发现这样会计算重复。见下图：

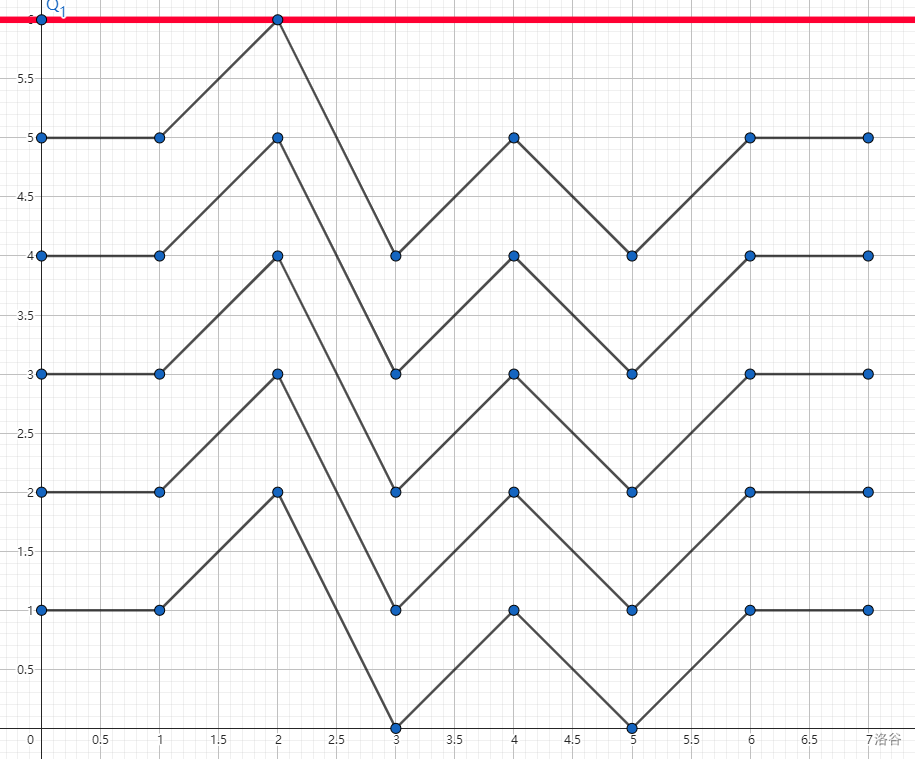
在这张图中，横坐标为操作数，纵坐标为盒子中黑球的数量，折线即为黑球的变化量，其中折线不能低于 x 轴，也不能高于我们规定的盒子中球的数量（也就是上图中的红线）。我们发现这样会被计算多次，我们就考虑去掉重复，只保留一条折线。我们就可以将红线向下平移一单位，保留下来的方案即为多计算的。见下图：

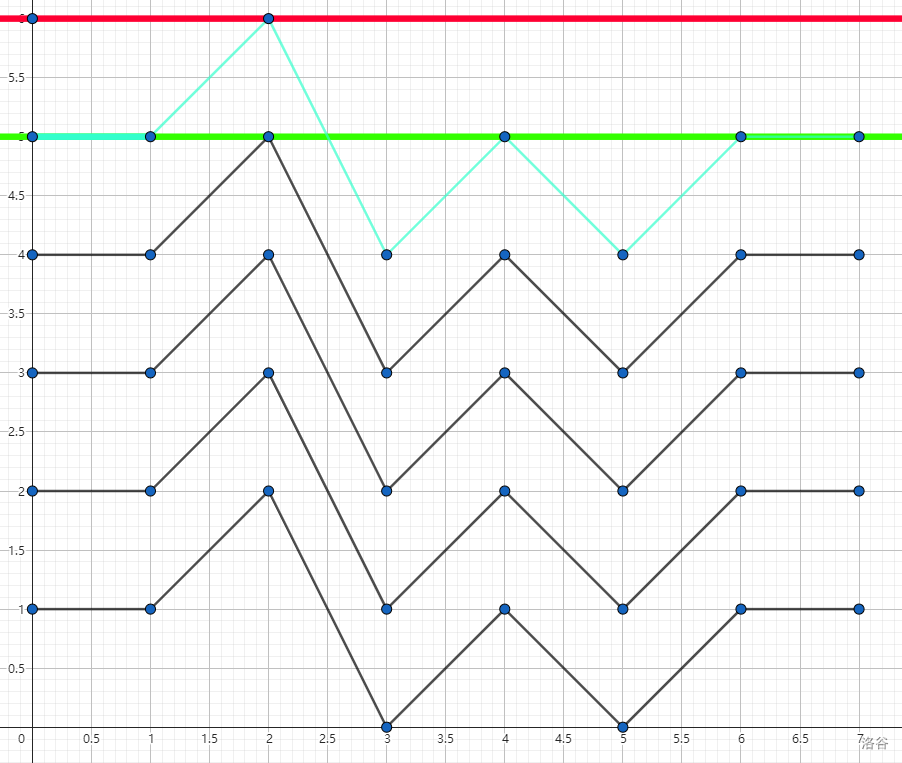
这样就可以避免重复计算。时间复杂度 \(O(n^2)\)。

方格染色

有一个 \(n\times m\) 的网格，每个格子可以被染成红色或蓝色。要求每个 \(2\times 2\) 的区域内每种颜色的个数必须是奇数。现在已经有 \(k\) 个格子被染色，求有多少合法的染色方案数。

数据范围：\(n, m, k\le 10^5\)。

---

有意思的找规律题。我们首先可以发现，如果这个网格的第一行和第一列确定后，整个网格就能被确定。因此我们就把问题转化为了对第一行和第一列的计数。我们发现一个 \(2\times 2\) 的区域中的数字异或起来必定为 \(1\)，稍微分析一下即可得到一个被染色的格子只会影响到第一行、第一列、原点构成的矩形的顶点。再找找规律就能找到这三个的异或关系。

这时我们就可以枚举原点的状态，然后把问题转化为 2-SAT，用边带权并查集即可。

城市规划

求 \(n\) 个点有标号连通图的个数。

数据范围：\(n\le 130000\)。

---

本题可能不是那么精妙，但是是下一道题的前置。

我们设 \(c_i\) 为 \(i\) 个点有标号连通图个数，\(\varphi(i)\) 为 \(i\) 个点的图的个数，易知 \(\varphi(x)=2^{\frac{x(x-1)}{2} }\)，只需要看点与点之间的边是否在图中即可。

我们考虑容斥，求出不连通图的个数。我们可以枚举一号点所在连通块的大小，就能得到转移方程

\[c(n)=\varphi(n)-\sum \limits _{i=1}^{n-1}\dbinom{n-1}{i-1}c_i\varphi(n-i) \]

这个转移方程右半部分的含义是：\(1\) 号点所在连通块的方案数为 \(c_i\)，同时我们需要选出 \(i-1\) 个点和它在一个连通块中。剩下的点就不用管了，形成任意的图都可以。

考虑加速计算这个式子：

\[\begin{aligned} c_n&=\varphi(n)-\sum \limits _{i = 1}^{n-1}\frac{(n-1)!}{(i-1)!(n-i)!}c_i\varphi(n-i)\\ \frac{c_n}{(n-1)!} &=\frac{\varphi(n)}{(n-1)!}- \sum \limits _{i = 1}^{n-1}\frac{c_i}{(i-1)!}\frac{\varphi(n-i)}{(n-i)!} \end{aligned} \]

设 \(\phi (x)=\frac{c(x)}{(x-1)!}\)，\(\pi (x)=\frac{g(x)}{x!}\)。那么上面的式子就变为了

\[\phi(n)=\frac{g(n)}{n!}-\sum \limits_{i=1}^{n-1}\phi (i)\pi(n-i) \]

直接分治 FFT 即可。时间复杂度 \(O(n\log^2 n)\)。

How Many of Them

求有 \(n\) 个点，割边数量不超过 \(m\) 的无向连通图的数量。

数据范围：\(n, m\le 50\)。

---

比较 nb 的不用多项式的图论计数。

我们设 \(F[i, j]\) 为 \(i\) 个点，\(j\) 条割边的无向连通图的数量。我们考虑去掉 \(1\) 号点所在的双连通分量，那么整张图就会分为一堆连通块。我们再设 \(G[i, j, k]\) 为 \(i\) 个点，\(j\) 条割边，\(k\) 个连通块的无向图的数量。那么我们枚举 \(1\) 号点所在连通分量的大小，就能对于 \(0<j<i\) 得到转移方程：

\[F[i, j]=\sum \limits _{p=1}^{i-1}(F[p, 0]\times\dbinom{i-1}{p-1}\times \sum \limits _{q=1}^j (G[i-p,j-q,q]\times p^q)) \]

\(p\) 枚举的是 \(1\) 号点所在连通分量的大小，\(q\) 枚举的是 \(1\) 号点所在的连通分量去掉后会剩下多少连通块，而割边也会随之减少 \(q\)，可以看下图理解：

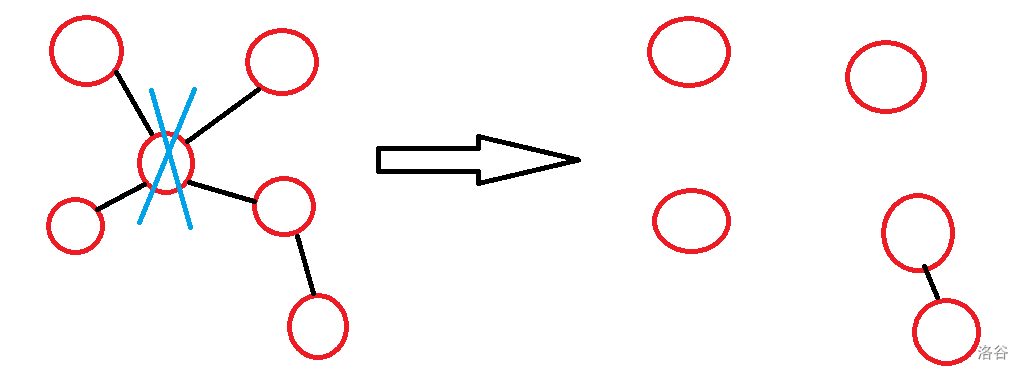
然后 \(p^q\) 的含义即为我们每个连通分量一定会选择 \(1\) 号点所在的连通块中一个点连边，那么方案数即为 \(p^q\)。

再考虑求出 \(F[i, 0]\)。根据容斥，我们只需要用连通图的数量减去含割边的图的数量即可，而连通图的数量则看上一道题。因此：

\[F[i, 0]=c_i-\sum \limits _{j=1}^{i-1}F[i,j] \]

最后我们再考虑求出 \(G\) 数组。我们依旧枚举 \(1\) 号点所在连通块大小 \(p\)，同时我们再枚举一号点连通块割边的数量 \(q\)，我们就能得到转移方程：

\[G[i,j,k]=\sum\limits_{p=1}^i\sum\limits _{q=0}^j(f[p,q]\times p\times \dbinom{i-1}{p-1}\times G[i-p,j-q,k-1]) \]

我们注意到其中多乘了一个 \(p\)，这其实代表着我们求出的是“有根双连通分量”，因为我们要在这个双连通分量中选一个点来和一开始去掉的边双连边。因此我们多乘了一个 \(p\)，而在别的情景中需要视情况而定。

时间复杂度：\(O(n^5)\)。

串珠子

有 \(n\) 颗珠子，所有的珠子互不相同，用整数 \(1\) 到 \(n\) 编号。对于第 \(i\) 个珠子和第 \(j\) 个珠子，可以选择不用绳子连接，或者在 \(c_{i,j}\) 根不同颜色的绳子中选择一根将它们连接。如果把珠子看作点，把绳子看作边，将所有珠子连成一个整体即为所有点构成一个连通图。特别地，珠子不能和自己连接。有多少种不同的方案将所有珠子连成一个整体。

数据范围：\(n\le 16\)。

---

我们回顾一下无向连通图的转移方程：

\[c(n)=\varphi(n)-\sum \limits _{i=1}^{n-1}\dbinom{n-1}{i-1}c_i\varphi(n-i) \]

我们本题可以类似的这样做。我们设 \(f_s\) 为 \(s\) 集合组成的无向连通图个数，\(g_s\) 为 \(s\) 集合组成的无向图个数。我们考虑 \(s\) 中第一个 \(1\) 所代表的点所在的联通块的集合，有如下转移：

\[f_s=g_s-\sum \limits f_tg_{\complement _s t} \]

而对于 \(g_s\)，我们只需枚举每条边看看是哪种状况即可。

时间复杂度 \(O(3^n)\)。

Uniformly Branched Trees

求有多少种 \(n\) 个点的不同构的树满足：除了度数为 \(1\) 的结点外，其余结点的度数均为 \(d\)。

数据范围：\(1 \le n \le 1000, 2 \le d \le 10\)。

---

我怎么选了这么多图论计数

本题和上面的图论计数不同的是，本题没有标号。因此我们需要有一个明确的规则来防止计算重复。

我们首先先选定一个根，使得这棵树比较特殊。我们很容易就可以发现可以选择重心作为根，因为树的重心最多只有 \(2\) 个，方便统计。而且这样它的子树大小都不超过 \(\frac{n}{2}\)。然后我们考虑如何计算方案。

我们设 \(f[i, j, k]\) 为 \(i\) 个节点，根有 \(j\) 个儿子，且子树大小都不超过 \(k\) 的方案数。当所有的子树大小都小于 \(k\) 时，方案数为 \(f[i-1, j, k-1]\)，直接加上。然后我们枚举有多少子树大小等于 \(t\)，这样除去这些子树的方案数即为 \(f[i-k\times t, j-t, k-1]\)，而这些大小为 \(k\) 的子树的总方案数可以看作是有 \(t\) 个相同的小球，放到 \(f[k, d-1, k-1]\) 个盒子里，盒子可空的方案数，直接插板法即可。因此转移方程为：

\[f[i, j, k]=f[i,j,k-1]+\sum \limits _{t\ge 1}(f[i-t\times k, j-t, k-1]\times \dbinom{f[k,d-1,k-1]+t-1}{t}) \]

根据重心的定义，答案即为 \(f[n, d, \frac{n}{2}]\)。但是我们有时候会重复计算，因为重心可能会有两个，在这时如果两个重心两边的树如果不同，那么就会被算重复。我们需要减去这些重复的方案，即 \(\dbinom{f[\frac{n}{2}, d-1, \frac{n}{2}-1]}{2}\)。这样就能统计完。

时间复杂度 \(O(n^2d^2)\)。

未完待续，持续更新