树相关题目整理
找了一些之前集训的题,还有一部分是 lyt 推荐的题目。因为发现自己树相关的题目太菜了,只能整理整理了。
货车运输
有 \(n\) 个城市和 \(m\) 条道路,每条道路有一个最大限重,运送的货物重量超过限重后就无法经过。现在有 \(q\) 辆货车要运输货物,每辆车只能走一次,第 \(i\) 辆车要从第 \(a_i\) 个城市运送到第 \(b_i\) 个城市。对每辆车求出最多能运送多少货物。
数据范围:\(n \le 10^4, m \le 5\times 10^4, q \le 3 \times 10^4\)。
根据贪心的思想,货车一定只会走最大生成树上的边。因此我们求出最大生成树,然后在这上面倍增或者树剖求最大值即可。
时间复杂度 \(O(n\log n)\)。
赛道修建
有 \(n\) 个路口,\(n-1\) 条道路,每条道路都有长度 \(w_i\),现在要修建 \(m\) 条赛道。每条赛道包含一条树上的路径,且每条道路只能被一条赛道经过。一条赛道的长度为包含所有道路的长度和。求出长度最小的赛道长度的最大值。
数据范围:\(n \le 5\times 10^4\)。
这种最小值最大的问法大部分都是二分。现在的关键就是 check 函数怎么写。
我们考虑在树上的一个节点,它的儿子有 4 种情况可以选择:和另一个儿子形成赛道、和父亲及以上路径形成赛道、不形成赛道、和当前到父亲这条边形成赛道。我们可以在每个节点记录一个向上传递的值,为这四种情况做准备。
第四种情况无疑是最优的,要直接选上。剩下的儿子我们两两配对,根据贪心的思想,要选择一个稍微小一些的儿子和它形成赛道,我们就可以用一个 set 查询后继。如果没有后继,就把它变为向上传递的值给父亲。最后判断是否选够 \(m\) 条赛道。这样就可以完成统计。
时间复杂度 \(O(n\log^2n)\)。
Exactly K Steps
给定 \(n\) 个节点的树,边权为 \(1\)。有 \(q\) 组询问,每组询问询问在树上是否存在与 \(u\) 距离为 \(k\) 的点,如果有,输出这个点。
数据范围:\(n,q \le 2\times 10^5\)。
根据反证法,我们可以证明树上某个点能够到达的最远点一定是树的直径的两个端点之一。因此我们可以以这两个端点分别建树,每次询问直接查询该点到根节点的距离。如果大于 \(k\) 则一定不存在,否则直接查找 \(k\) 级祖先即可。
时间复杂度 \(O(n + q\log n)\)。
树网的核
定义偏心距:\(\mathrm{ECC} (F)\) 为树中所有点到 \(F\) 这条路径的最远距离的最大值。对于一颗给定的边有边权的树,求出对于所有在直径上且长度不大于 \(s\) 的路径中的最小偏心距。
数据范围:\(n \le 300, s \le 1000\)。
我们可以先通过两次 bfs 求出树的直径。然后枚举这条直径上的路径。根据贪心的思想,我们一定是要让这个路径越长越好,因此我们已知该路径的一个端点,就能知道另一个端点的位置。然后再求出偏心距即可。时间复杂度 \(O(n^2)\)。
另外本题有 \(O(n)\) 的做法,但是我不会。
Fib-tree
给定一棵树,其满足是一颗 \(\mathrm{Fib-tree}\) 必须满足以下两个条件之一:大小为 \(1\);将其沿一条边分开后形成的两棵树仍然都为 \(\mathrm{Fib-tree}\)。现在有一颗大小为 \(n\) 的树,判断它是否为 \(\mathrm{Fib-tree}\)。
数据范围:\(n \le 2\times 10^5\)。
我们可以对树找出它的重心。设该树大小为 \(fib_i\),因为树的重心的性质(子树大小不超过 \(\frac{n}{2}\)),该重心的子树中至多会包含 \(2\) 个大小为 \(fib_{i-2}\) 的子树,我们就可以砍掉任意一颗子树(剩下的一颗 \(fib_{i-2}\) 的子树必然也是要被分开的),对分出来的树分别递归即可。
因为斐波那契数的增长速度,我们可以证明切的次数至多为 \(\log n\) 次,因此总复杂度为 \(O(n\log n)\)。
Tree Painting
给定一颗大小为 \(n\) 的树,初始树中全为白点,现在进行 \(n\) 次操作,每次可以选择一个和黑点相邻的点将其染黑,同时获得与该点在染色之前所在的白色连通块大小相同的权值。第一次操作可以任意选点。求能获得的最大权值。
数据范围:\(n \le 2\times 10^5\)。
我们可以把第一次选择的点设为该树的根,接下来我们所做的所有操作就能转化为:选择一个子树,获得该子树大小的权值。这样就可以求出某个点作为根时的权值了。
接下来就是一个简单的换根 dp,稍微推推式子就可以得出 \(ans[v] = ans[u] + n - 2 \times siz[v]\)。时间复杂度 \(O(n)\)。
Centroids
给定一棵树,现在有一次改造树的机会,可以将一条边断掉,再连上一条边。问有多少点可以通过这个操作成为该树的重心。
数据范围:\(n \le 4\times 10^5\)。
考虑改造树的操作的实质,就是把一棵子树扔到另一个点上去。再考虑重心的性质:子树大小都不超过 \(\frac{n}{2}\)。
我们对于每个点来考虑,当它有大小有超过 \(\frac{n}{2}\) 的子树时,我们可以找下这颗子树中最大能拆走的,且大小不超过 \(\frac{n}{2}\) 的子树。我们就可以用这个来 dp。
设 \(dp[i]\) 为子树中最大能拆走的且大小不超过 \(\frac{n}{2}\) 的子树大小。再设 \(f[i]\) 为子树外最大能拆走的且大小不超过 \(\frac{n}{2}\) 的子树大小。
\(dp[i]\) 比较好求,我们主要考虑 \(f[i]\)。我们可以从上往下求出每个点的 \(f\)。但是这时我们发现可能某个节点的父亲的 \(dp\) 就是从这个节点转移过来的,我们可以记录一个 \(dp\) 的最大值 \(dp[u][0]\),一个 \(dp\) 的次大值 \(dp[u][1]\)。当该节点是转移点时用 \(dp[fa][1]\) 来更新 \(f[u]\),否则用 \(dp[fa][0]\) 更新。
时间复杂度 \(O(n)\)。
HXY造公园
有 \(n\) 个休息点和 \(m\) 条双向道路,保证没有环。现在有两种操作:询问 \(x\) 点所在的连通块中的最长简单路径;将 \(x\) 和 \(y\) 所在的连通块连接起来,假如已经连通则忽视,否则在两个连通块间加一条边,使得形成的新连通块中最长简单路径最短。
数据范围:\(n, q \le 3\times 10^5\)。
比较裸的树的直径的题。首先一个显然的结论是在两棵树之间连边,使得树的直径最小的连边方法是连接两棵树直径的中点,形成新树的直径即为 \(\left \lceil \frac{n_1}{2} \right \rceil +\left \lceil \frac{n_2}{2} \right \rceil +1\)。有了这个性质,我们在一开始对每棵树都求一遍树的直径,然后连边就按照这个公式算即可。用并查集维护连通性。
时间复杂度 \(O(n)\)。
巡逻
有 \(n\) 个村庄和 \(n-1\) 条道路连接这些村庄。警察局在 \(1\) 号村庄,警察每天会去巡逻,经过每条边至少一次,最后回到警察局。现在要新修建 \(k\) 条道路,并且这些新道路每天要恰好经过一次。经过一条边的时间为 \(1\)。问修建了这两条路后巡逻的最短长度。
数据范围:\(n\le 10^5, k\le 2\)。
我们先考虑 \(k=1\) 的情况,新修建一条道路后,这条道路所覆盖的树上的路径都会少走一次,因此我们就可以贪心的选择在树的直径的端点间修建第一条道路。设直径长度为 \(L_1\),则答案即为 \(2(n-1)-L_1+1\)。
而当 \(k=2\) 时,我们可以进行分类讨论:
- 第二条道路不在第一条道路形成的环中
- 第二条道路在第一条道路形成的环中
第一种情况的话可以直接类比 \(k=1\) 的情况,贪心即可。而第二种情况则需要分析一下。因为新修建的道路必须走一次,我们必须再走一遍第二条道路所覆盖的边,也就是第一次的少走一次中有一段还要走两次。为了抵消这些,我们可以把直径上的边权都设为 \(-1\)。用树形 dp 求出直径 \(L_2\),答案即为 \(2(n-1)-(L_1-1)-(L_2-1)\)。
时间复杂度 \(O(n)\)。
严格次小生成树
给定一张图,求出这张图的严格次小生成树。
数据范围:\(n \le 10^5, m\le 3\times 10^5\)。
首先有一个结论:严格次小生成树和最小生成树的边集中不同的元素仅有 \(1\) 个。这个结论用反证法即可证明。
利用这个结论,我们可以先求出最小生成树,考虑在最小生成树上加入一条边再去掉一条边。我们记录一个路径上最大值和次大值,加入边时要把最大值或次大值替换掉,从而替换成这条边。这部分可以用树上倍增实现。这样枚举每条边,对每条边求一遍,就可以求出严格次小生成树。
时间复杂度 \(O(m\log n)\)。
保卫王国
有 \(n\) 个城市,\(n-1\) 条道路,现在要驻扎军队,要求每条边的两个端点中至少要有一个城市驻扎军队。在第 \(i\) 个城市驻扎军队要花费 \(p_i\) 元。
现在有 \(q\) 次询问,每次询问规定两个城市是否驻扎军队,然后回答当前驻扎军队花费的最小值。询问和询问之间相互独立。
数据范围:\(n, q\le 10^5\)。
本题有动态 dp 的做法,但是不在讨论范围内。
我们先考虑如果没有强制选择的要求,这题就是一个比较简单的树形 dp,设 \(f[i][0/1]\) 为 \(i\) 子树中这个点选择/不选择驻扎军队的最小花费,转移为:
我们可以发现,如果强制规定的两个点 \(u\) 和 \(v\) 的状态,那么受影响的转移只有 \(u\) 到 \(lca\),\(v\) 到 \(lca\),以及 \(lca\) 到根的路径上的点。我们就可以用树上倍增来维护这个东西。
我们设 \(fh[i][j][0/1][0/1]\) 为 \(i\) 的第 \(2^j\) 祖先(以下称为 \(anc\))的子树中除去 \(i\) 的子树,且 \(i\) 的状态为 \(0/1\),\(anc\) 的状态为 \(0/1\) 时的最小花费。这个可以很简单的用倍增求出。之后我们在将 \(u\to lca\) 和 \(v\to lca\) 这两条路径倍增转移时,我们枚举祖先的状态然后进行转移。
同时,因为将 \(u\) 和 \(v\) 转移到 \(lca\) 之后还要继续向上转移,同时还要加上其他树的贡献,我们再设 \(g[i][0/1]\) 为整棵树除去 \(i\) 的子树,且 \(i\) 的状态为 \(0/1\) 的最小花费。这个数组可以直接 dp 求出。
最后倍增到 \(lca\) 的儿子之后,我们再枚举 \(lca\) 选或不选,同时加上除去 \(lca\) 其他子树的贡献,即为答案。
时间复杂度 \(O(n\log n+q\log n)\)。
倍增部分代码:
inline int solve(int x, int a, int y, int b)
{
if(dep[x] < dep[y]) swap(x, y), swap(a, b);
int tx[2] = {INF, INF}, ty[2] = {INF, INF};
int nx[2], ny[2];
tx[a] = f[x][a], ty[b] = f[y][b];
for(int i = 18; i >= 0; i -- )
{
if(dep[fa[x][i]] >= dep[y])
{
nx[0] = nx[1] = INF;
for(int u = 0; u < 2; u ++ )
for(int v = 0; v < 2; v ++ )
nx[u] = min(nx[u], tx[v] + fh[x][i][v][u]);
tx[0] = nx[0], tx[1] = nx[1];
x = fa[x][i];
}
}
if(x == y) return tx[b] + g[x][b];
for(int i = 18; i >= 0; i -- )
{
if(fa[x][i] != fa[y][i])
{
nx[0] = nx[1] = ny[0] = ny[1] = INF;
for(int u = 0; u < 2; u ++ )
for(int v = 0; v < 2; v ++ )
{
nx[u] = min(nx[u], tx[v] + fh[x][i][v][u]);
ny[u] = min(ny[u], ty[v] + fh[y][i][v][u]);
}
tx[0] = nx[0], tx[1] = nx[1];
ty[0] = ny[0], ty[1] = ny[1];
x = fa[x][i];
y = fa[y][i];
}
}
int lca = fa[x][0];
int ans0 = f[lca][0] - f[x][1] - f[y][1] + tx[1] + ty[1] + g[lca][0];
int ans1 = f[lca][1] - min(f[x][1], f[x][0]) - min(f[y][0], f[y][1]) + min(tx[0], tx[1])
+ min(ty[0], ty[1]) + g[lca][1];
return min(ans0, ans1);
}
灾难
有 \(n\) 种生物,如果生物 \(x\) 可以吃生物 \(y\),则从 \(x\) 向生物 \(y\) 连一条有向边。这样就会形成一个叫食物网的图。这张图无环。有的点没有入点,这些生物是生产者,依靠光合作用生存。如果一种生物的所有食物都灭绝了,那它也会跟着灭绝。
我们定义一种生物的灾难值为如果它突然灭绝,那么会一起灭绝的生物种数。给定一个食物网,求出每种生物的灾难值。
数据范围:\(n\le 65534\)。
我们可以先建立一个超级源点(太阳),向所有的生产者连边,表示所有生产者依靠它活着,因此这个超级源点的灾难值即为 \(n\)。
我们先考虑一个特殊情况:如果给定的食物网是一棵树,那么一个节点的灾难值一定就是它的子树大小。这启示我们可以把给定的 DAG 转化为树来计算。
有一个显而易见的结论是,如果某种生物的食物有超过 \(2\) 种时,我们将其连到它所有的食物的 \(lca\) 上是等价的。因为如果一种它的食物灭绝了不会对它造成影响,但是当这些食物的 \(lca\) 或更靠上的物种灭绝时,它所有的食物都会灭绝,它也就因此灭绝了。所以我们可以维护一颗灭绝树,当新加进来点时,我们可以把它的食物求一个 \(lca\),然后把它挂到 \(lca\) 上。因为这棵树是在不断加入点的,所以我们要采用倍增的方法求 \(lca\)。
时间复杂度 \(O(n\log n)\)。
宝石
给定 \(n\) 个城市,城市之间有 \(n-1\) 条道路相连接。有 \(m\) 种宝石,第 \(i\) 座城市会出售第 \(w_i\) 种宝石。K 神有一个宝石收集器,它能按顺序收集 \(c\) 颗宝石,按顺序为 \(P_1,P_2\cdots P_c\)(\(P_i\) 互不相等)。K 神到达一个城市后,如果该城市出售的宝石和当前收集器需要放进去的宝石种类相同,则会购买一颗并将其放入收集器中。否则他只会经过这个城市。
现在有 \(q\) 次询问,每次询问从 \(s\) 点沿最短路径到 \(t\) 点收集器所能收集到的宝石数量。
数据范围:\(n,q\le 2\times 10^5\)。
我们可以把宝石按顺序重新编号一下。第 \(P_i\) 种宝石被重新标号为 \(i\),剩下的宝石随意编号。这样我们的问题就转化为了求一个最大的 \(cnt\) 满足 \(cnt \le c\) 且从 \(s\) 到 \(t\),\(1\sim cnt\) 依次出现。
我们先把一段路径拆成两端:\(s\to lca\) 和 \(lca \to t\)。第一段可以用树上倍增的方法做。我们设 \(f_1[u][i]\) 为 \(u\) 到根的路径中距离它最近的,且出售宝石种类为 \(w_u+2^i\) 的城市在哪。可以用主席树查询 \(u\) 到根节点的路径上第一个 \(1\) 的出现位置,这样就解决了向上走的链。
而向下走的链显然是有单调性的,如果 \(cnt\) 可以满足,那么 \(cnt-1\) 也必定可以满足。我们就可以采取二分的方法,二分最后到达的时候的 \(cnt\)。我们设 \(f_2[u][i]\) 为 \(u\) 到根的路径中距离它最近的,且出售宝石种类为 \(w_u-2^i\) 的城市在哪。这样我们也就可以向上跳,跳到要衔接的地方看看能不能衔接上即可。
时间复杂度 \(O(n\log n + q\log^2n)\)。
The Cow Gathering P
有 \(n\) 个人,\(n-1\) 对人互为朋友。离场时,每个人都希望当至少还有两个人未离开时,剩下的每个人都至少有一个朋友在场。并且有 \(m\) 条限制关系,使得 \(a_i\) 这个人必须比 \(b_i\) 先走。求出每个人是否能成为最后一个离场的人。
数据范围:\(n, m \le 10^5\)。
一个显然的性质是:对于一个限制关系 \(a_i\) 比 \(b_i\) 先走,当 \(b_i\) 为根时,\(a_i\) 的一整颗子树都不能成为最后走的。这启发我们将人从可以最后走的集合中一个一个删去。
我们确定一个根后,单独考虑一对限制关系 \((a_i,b_i)\)。当 \(b_i\) 在 \(a_i\) 的子树外时,\(b_i\) 为根时 \(a_i\) 的子树不变,我们直接把它的子树全部置为 \(0\) 即可。而当 \(b_i\) 在 \(a_i\) 的子树内时(这个可以用 dfn 序 \(O(1)\) 判断),我们需要把除了 \(a_i\) 所在的子树之外的所有点全部置为 \(0\)。找 \(a_i\) 所在子树对应着 \(b_i\) 的哪个儿子可以直接查询 \(dep[a]-dep[b]-1\) 级祖先来获得。
对于子树置零操作,我们可以直接在 dfn 序上差分,类似于树剖的实现方式。
但是我们还少了一种情况:无解。我们可以直接在树上判断树中的有向边是否出现了环,如果出现了环,则为无解的情况。
因此总时间复杂度 \(O(n\log n)\)。
Christmas Game
Alice 和 Bob 在一棵 \(n\) 个点的树上玩游戏,第 \(i\) 个节点上有 \(a_i\) 个石子,每轮可以选择一个深度至少为 \(k\) 的节点并移动任意多石子到其 \(k\) 级祖先处,当一个节点不存在 \(k\) 级祖先时无法移动。Alice 先手,对每个结点询问如果将其作为根谁会赢。
数据范围:\(n\le 10^5 , k\le 20 , a_i\le 10^9\)。
有意思的博弈论题。树上每个点可以被移动 \(\left \lfloor \frac{dep_u}{k} \right \rfloor\) 次,我们就把这一堆石子拆开来看,一堆石子拆成相同的 \(\left \lfloor \frac{dep_u}{k} \right \rfloor\) 堆石子。然后就可以直接 Nim 游戏,因为偶数堆相同的全部异或没了,我们就只需要考虑 \(\left \lfloor \frac{dep_u}{k} \right \rfloor\) 为奇数的节点上的石子,当这些石子异或为 \(0\) 时,先手必败。
我们就可以考虑树形 dp。设 \(f[i][j][0/1]\) 为 \(i\) 子树中深度 \(\bmod k = j\) 且 \(\left \lfloor \frac{dep_u}{k} \right \rfloor \bmod 2 = 0/1\) 的所有点权值的异或和。这个可以通过简单的树形 dp 解决。然后再考虑换根。因为异或具有可减性,换根时只需要把当前子树中的贡献减去,然后再重复类似树形 dp 的方法就可以把每个点为根的信息都搞出来了。最后把 \(f[u][i][1]\) 全部异或起来来判断是否先手必胜即可。
时间复杂度 \(O(nk)\)。
Phoenix and Earthquake
给定 \(n\) 个点,\(m\) 条无向边的图,每个点有点权 \(a_i\)。如果一条边 \((u, v)\) 满足 \(a_u+a_v\ge x\),则可以把这两个点缩成一个点,新点的点权为 \(a_u+a_v-x\)。问整张图是否最终能被缩成一个点。
数据范围:\(n,m\le 3\times 10^5\)。
考虑无解的情况。无解的情况仅有两个:图不连通或者 \(\sum a_i < (n-1)x\)。因为我们一定可以按照下面的构造方法构造出一组合法解。
我们首先求出该图的任意一颗生成树,然后在这颗生成树上进行操作(因为所有的操作执行完后这些边一定是一颗生成树)。
我们考虑用数学归纳法,显然当 \(n=2\) 时是成立的。当 \(n > 2\) 时,我们考虑叶子节点 \(u\)。当 \(w[u] \ge k\) 时,我们可以直接把它和父亲节点缩成一个点,这时让 \(w[fa]\gets w[u]+w[fa]-x\)。而当 \(w[u] < k\) 时,我们把它留到最后缩起来,而剩下的大小为 \(n-1\) 的树的权值必定大于 \((n-2)x\)(因为 \(w[u] < k\))。根据数学归纳法,结论成立。
有了这个证明方法,构造方法也就出来了。我们维护一个队列和一个栈。当 \(w[u] \ge k\) 时把它扔到队列里,否则扔到栈里面。最后按照队列、栈的顺序输出即可。
时间复杂度 \(O(n)\)。
Magic Matrix
给定一个大小为 \(n\times n\) 的矩阵 \(a\),它是魔法矩阵当且仅当满足以下条件:
-
\(\forall i\in[1,n],a_{i,i}=0\)
-
\(\forall i,j\in[1,n],a_{i,j}=a_{j,i}\)
-
\(\forall i,j,k\in[1,n],a_{i,j}\le\max(a_{i,k},a_{j,k})\)
判断矩阵 \(a\) 是否为魔法矩阵。
数据范围:\(n \le 2500\)。
前两个条件可以直接 \(O(n^2)\) 做,但是第三个条件枚举显然是不行的(除非你用什么 bitset 来优化暴力),因此我们就需要发现一些性质。
先看前两条限制,我们会发现它很像一种东西:邻接矩阵。我们就可以把它转化成一个图论问题。我们再来考虑下第三个限制:
我们根据这个式子,就能得出如何判定:对于每一个 \(a_{i,j}\),\(\forall i,j,k\in[1,n],a_{i,j}\le\max(a_{i,k},a_{j,k})\) 条件满足就等价于将图中所有小于 \(a_{i,j}\) 的边加入后,\(i\) 和 \(j\) 不连通。因此我们就可以跑最小生成树,在跑的过程中判断一下即可。
时间复杂度 \(O(n^2\log n)\)。
The Shortest Statement
\(n\) 个点,\(m\) 条边的无向连通图。有 \(q\) 次询问,第 \(i\) 次询问回答从 \(u\) 到 \(v\) 的最短路的长度。
数据范围:\(n,m,q\le 10^5, m-n \le 20\)。
观察到题目中 \(m-n\le 20\) 的性质,我们可以考虑利用一下。
我们可以求出最小生成树,把没有用到的边先记录一下。对于每次询问,我们可以把它分成两类路径的最小值:树上路径、经过没有用到的边的路径。我们把没有用到的边所连接的点称为关键点,则第二类路径一定会经过关键点来中转(至于中转到树边还是非树边则是程序自己的事情)。
我们可以在 \(O(\log n)\) 的时间内求出树上的路径大小,剩下的经过关键点的路径我们需要每个关键点跑一次最短路,然后枚举关键点,计算 \(dist_{u, i} + dist_{i, v}\)。最后取 \(\min\) 即可。
时间复杂度 \((m-n)n\log n\)。
春节十二响
“春节十二响”由 \(n\) 个子程序构成,第 \(i\) 个子程序所需的内存空间是 \(M_i\)。这 \(n\) 个子程序之间的调用关系构成了一棵以第 \(1\) 个子程序为根的树,其中第 \(i\) 个子程序在调用树上的父亲是第 \(f_i\) 个子程序。
由于内存紧张,电力控制芯片上提供了一种内存分段机制。你可以将内存分为若干个段 \(S_1\), \(S_2\), ..., \(S_k\),并将每个程序预先分配到一个固定的段。如果两个子程序没有直接或间接的调用关系,则他们可以被分配到同一个段中,反之则不能。换言之,当且仅当 \(a\) 和 \(b\) 在调用树上不是祖先—后代关系,\(a\) 和 \(b\) 可以被分配到同一个段中。
一个段的大小应当是所有分配到这个段的子程序所需内存大小的最大值,所有段大小的和不能超过系统的内存大小。
现在艾莉芬想要知道,电力控制芯片至少要有多少内存,才能保证春节十二响的正确运行。即:最少需要多大的内存,才能通过先将内存分成若干个段,再把每个子程序分配到一个段中,使得每个段中分配的所有子程序之间不存在祖先—后代关系。
数据范围:\(n \le 2\times 10^5\)。
根据贪心的思想,我们必然是要让大的程序和大的程序分配到一个段中,我们考虑如何在树上实现这一点。
我们对于每个点维护一个堆,堆内存储的是该节点的子树中所有的段。传递到 \(u\) 时,我们把所有子树的最大值拿出来拼成一个新的段,最后剩余的再插回去即可。这样暴力合并的复杂度是 \(O(n^2\log n)\) 的,不能承受。
我们可以考虑一个东西:树上启发式合并。每次将小的集合合并到大的集合,用这个来合并这些堆就可以把复杂度降到 \(O(n\log^2n)\)。
Blood Cousins Return
给定一片森林,每次询问一个节点的 K-Son 共有个多少不同的名字。一个节点的 K-Son 即为在该节点子树内的,深度是该节点深度加 \(K\) 的节点。
数据范围:\(n, m\le 10^5\)。
每次询问都处理一遍复杂度太高,考虑离线下来做。
我们假设当前正在处理 \(u\) 的子树,我们先考虑递归处理它所有的轻儿子,同时防止混淆,处理完后把数据清空。然后直接递归重儿子,不清空数据,再把轻儿子的数据加上。这样就可以轻易地统计出有关 \(u\) 点子树内的答案。这样也叫做树上启发式合并,时间复杂度 \(O(n\log^2n)\)。
Yuezheng Ling and Dynamic Tree
给定一颗有 \(n\) 个节点,以 \(1\) 为根的树,\(i\) 号点的父亲为 \(a_i\)。其中对于 \(2\sim n\) 号点,\(a_i<i\)。现在有两个操作:
- 令 \(a_i=\max(1,a_i-x)\)(\(l\le i \le r\))。
- 查询在现在 \(a\) 数组所构成的树中,\(u\) 与 \(v\) 的 \(lca\)。
数据范围:\(n,q,x\le 10^5\)。
树形结构无法维护这种区间换父亲的操作,我们考虑万能算法:分块。
我们对于每个点,维护一个 \(b_i\),表示这个点一直向上跳父亲,第一次跳出块的点的编号。当 \(pos[a_i] \not= pos[i]\) 时,\(b_i=a_i\),否则 \(b[i]=b[a_i]\)。
先考虑修改操作。散块直接暴力修改重构即可,对于整块,我们发现当执行操作的次数大于 \(\sqrt n\) 时,所有点第一次就能跳出块,这时就不需要暴力重构维护块内点的 \(b_i\)。因此我们只需要记录一个 \(f_x\) 和 \(cnt_x\),分别表示第 \(x\) 块修改的懒标记和被操作了多少次。因为每个块最多暴力重构 \(\sqrt{n}\) 次,所以修改的复杂度为 \(O(n\sqrt n)\)。
再考虑查询 \(lca\) 操作,我们可以发现这个分块十分像树链剖分的重链。我们就可以类比倍增以及树链剖分的 \(lca\) 求法。进行一个分类讨论:
-
当 \(pos[x]\not=pos[y]\) 时,让 \(pos\) 大的点跳 \(b\)。
-
否则让 \(x\) 和 \(y\) 同时跳 \(b\),直到跳到两个点下一次要跳的 \(b\) 相同。
-
最后让编号大的点不断跳 \(a\),直到 \(x=y\)。
此时 \(x\) 即为 \(lca\)。复杂度 \(O(q\sqrt n)\)。
Crash 的文明世界
给定一棵树,对于每个点 \(u\),求出 \(\sum\limits _{i=1}^n dist_{u,i}^k\)。
数据范围:\(n \le 5\times 10^4, k \le 150\)。
一个偏数学的题,开始推式子。
因此我们只需要求出 \(f_{u,j}=\sum\limits _{i = 1}^n\dbinom{dist_{u,i}}{j}\) 即可。根据组合数 \(\dbinom{n}{m}=\dbinom{n-1}{m}+\dbinom{n-1}{m-1}\) 的性质,我们可以得到这个转移方程:
这样就能求出一个根的答案。剩下的答案换根 dp 即可。
时间复杂度 \(O(nk)\)。
Two Trees
给定两棵大小均为 \(n\) 的树,点都从 \(1\sim n\) 编号。我们要给每个点一个权值,使得两棵树上都满足每个点的子树中权值和为 \(1\) 或 \(-1\)。如果无解输出 IMPOSSIBLE。
数据范围:\(n\le 10^5\)。
显然的判无解的方式是:在两棵树中相同节点的子节点个数奇偶性不一致。当子节点有奇数个时,该节点要填 \(0\),否则填 \(1\) 或 \(-1\)。因此这样是无解的。
考虑如何构造出一组合法的方案。我们先用一个超级源点把根连起来,再将所有度数为奇数的点向在另一棵树上的相同点连边,这样所有点的度数就都为偶数了。我们从源点跑欧拉回路,一开始度数为偶数的点的权值必然是 \(0\),而一开始度数为奇数的点的权值就需要看欧拉路定向后的方向了。我们令从 \(1\) 号树连向 \(2\) 号树的边对应点的权值为 \(1\),否则为 \(-1\)。这样就完成了构造。
考虑这种构造方法的正确性:
对于每一个点来说,我们把经过它的欧拉路分为两类:一直在它子树内,没有经过父亲的;从它出发,绕一圈后从父亲回来。对于第一种,在它子树中可能会出现很多,但是因为会从一棵树走到另一棵树,再走回来一次,这两次的正负一直接抵消掉。而对于第二种路径,它的父亲到它自己只有一条路径,而父亲也没有在它的子树内,因此在它子树内一定有且仅有一个 \(1\) 或 \(-1\) 没有被抵消掉。这样就能够证明所有的子树内权值都为 \(\pm 1\)。
Tree Edges XOR
给定一棵大小为 \(n\) 的树,保证 \(n\) 为奇数。每条边有一个权值 \(w_{1, i}\) 和目标权值 \(w_{2, i}\)。现在可以任意次地把与一个边相连的其他边的权值异或上这条边的权值,求是否能让每条边的权值都变为目标权值。
数据范围:\(n \le 10^5\)。
我们可以把边权转化为点权,但是这题和普通的边权转点权不太一样,本题中的点权为它到我们选定的根的距离(这里我选定 \(1\) 号点为根)。由于一条边的边权可以由相邻的两个点的距离异或得到,因此距离的集合和边权的集合是一一对应的。
我们考虑我们进行一次操作会造成什么影响。
见下图:
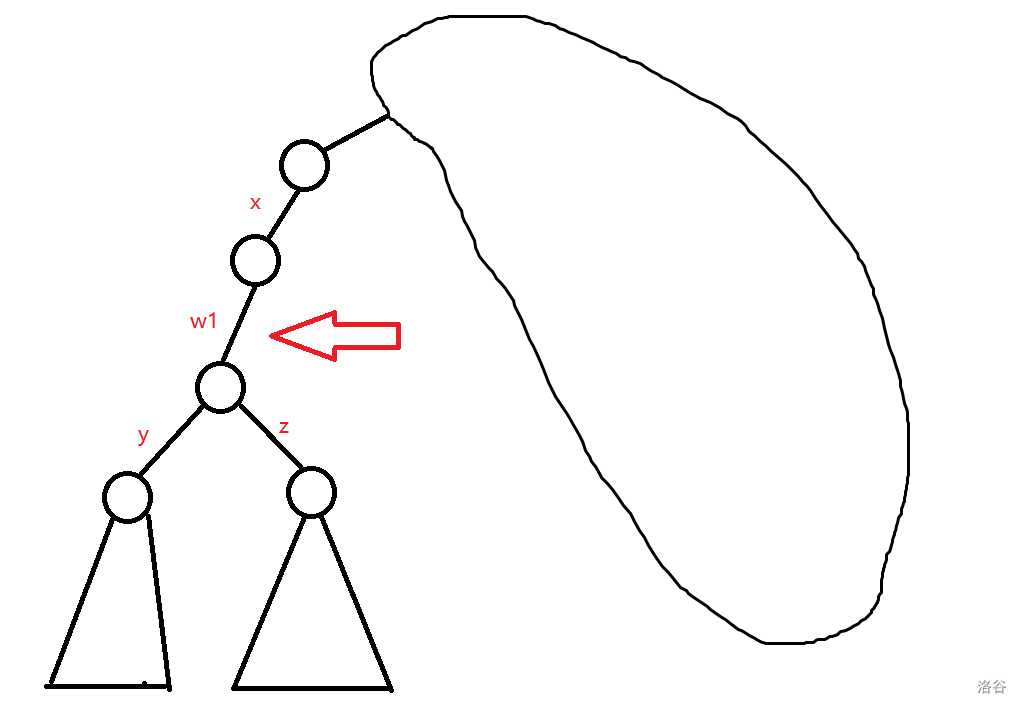
我们对这条边进行操作,操作过后我们可以发现,这个操作的边上面的点连的边的边权变为 \(x \oplus w_1\)(这里我用 \(\oplus\) 表示异或),下面的边的边权分别为 \(y\oplus w_1, z\oplus w_1\)。我们会发现,除了这两个点的距离之外,别的点的距离都不会改变。因为在这个操作的边的子树外肯定不会变,在子树内因为到根的路径会多两个 \(w_1\) 来异或,因此也不会变。
于是我们就考虑一下操作涉及到的这两个点的距离怎么改变。我们可以发现,上面的那个点的距离操作前为 \(a\),操作后为 \(a\oplus w_1\)。下面这个点的距离操作前为 \(a\oplus w_1\),操作后由于路径上有两个 \(w_1\),则距离为 \(a\)。因此,一次操作只会交换相邻两个点的点权,也就是距离。
但是我们可以发现一些不对劲的地方,比如说,如果我们把一个点和根节点操作,理论上会交换它们的距离,但是根节点的距离应该始终为 \(0\),这就出现了问题。我们为了修正这个问题,我们可以引入一个虚拟节点来向根节点连边。而一号点进行操作时也会改变这条边的边权。这样也就符合了我们上面的结论:每次操作交换两个点的距离。
现在就是如何判定的问题了。我们发现,唯一棘手的地方就是在这个虚拟节点和根节点之间的边的边权上,我们暂且把它称为虚拟边,只要把这一点解决了即可。我们可以发现,由于每次只会交换两个点的点权,点权的集合是不改变的,因此我们可以从第一棵树中得到第二棵树中有虚拟边的情况下所有点的距离的异或和,而我们又能得到第二棵树中没有虚拟边的情况下所有点的距离。同时,由于题目中的一个条件:\(n\) 为奇数,因此我们就能得到第二棵树中虚拟边的权值,只需要异或一下即可。
这样我们就能求出第二棵树中所有点在有虚拟边的情况下所有点的距离。判断第一棵树和第二棵树中这个集合是否相等即可。
Complete the MST
给定一个 \(n\) 个节点的完全图,有 \(m\) 条边给定边权,剩下的边没有给定,可以任意定非负整数的边权。同时还要满足所有边的权值异或起来等于 \(0\)。求所有可能的赋值方案中最小生成树的权值的最小值。
数据范围:\(n, m\le 2\times 10^5\)。
首先一个显而易见的结论是:新定的边权只有 \(1\) 条的边权非零。这点用 \(\sum x_i \ge \oplus x_i\) 就可以证明。因此我们只需要看哪一条边的权值附为所有给定边权的异或值,我们记作 \(x\)。
下面就开始大力分类讨论:
- 未给定的边能构成一个环
这种情况下,我们只需要在这个环上选择一条边边权为 \(x\),用剩下的边去构成最小生成树。这时我们把所有未给定的边构成的连通块跑出来缩成一个点,跑最小生成树即为答案。
- 未给定的边不能成环
我们把给定权值的边分为三类:一定在最终 MST 中的、一定不在的、其他。第一类即为我们上面那种情况所说的,第二类也肯定不在原图的 MST 中,而第三类就是我们要考虑的。
由于在没有确定边权的边构成的图中,值为 \(x\) 的边是不确定的,就像是离域 \(\pi\) 键一样,因此我们找到最小的第三类边,与 \(x\) 比较是否会进入最小生成树即可。

