十二重计数法

题目地址

十二重计数法作为组合数学登峰造极之作之一，我觉得有必要写一下所有情况的做法以及数学推导来整理一下。

球之间互不相同，盒子之间互不相同

本情况中，每个小球都有 \(m\) 个盒子的选择，因此根据乘法原理，总的方案数即为 \(m^n\)。用快速幂计算，复杂度 \(O(\log n)\)。

球之间互不相同，盒子之间互不相同，每个盒子至多装一个球

当 \(n > m\) 时，盒子放不完小球，方案数为 \(0\)。

当 \(n \le m\) 时，仍然是考虑每个小球：

第一个小球有 \(m\) 种选法，第二个小球有 \(m-1\) 种选法，第三个小球有 \(m - 2\) 种选法， \(\cdots\)，第 \(n\) 个小球有 \(m - n + 1\) 种选法。根据乘法原理，总方案数为 \(\frac{m!}{n!}\)，或者可以写成 \(m^{\underline{n} }\)。时间复杂度为 \(O(n)\)。

球之间互不相同，盒子之间互不相同，每个盒子至少装一个球

设 \(f(n, m)\) 为将 \(n\) 个小球放入 \(m\) 个盒子，且没有空盒子的方案数。

设 \(g(n, m)\) 为将 \(n\) 个小球放入 \(m\) 个盒子，且可以空盒子的方案数。

我们要求的是 \(f(n, m)\) 的值，但是我们可以先用 \(f\) 表示 \(g\)。

枚举空盒子的数量，然后我们就可以得到下面的方程：

\[g(n, m)=\sum \limits_{i=0}^{m} \dbinom{m}{i} f(n,i) \]

这里我们发现有二项式系数，我们可以考虑二项式反演。

先给出二项式反演的公式：

\[g(n)=\sum \limits_{i=0}^{n} \dbinom{n}{i}f(i) \Leftrightarrow f(n)=\sum \limits_{i=0}^n \dbinom{n}{i}(-1)^{n-i}g(i) \]

---

证明过程：

已知：\(f(n)=\sum \limits_{i=0}^{n} \dbinom{n}{i}g(i)\)

证明：

\[\begin{aligned}\sum \limits_{i=0}^n\dbinom{n}{i}(-1)^{n-i}f(i)&=\sum \limits_{i=0}^n\dbinom{n}{i}(-1)^{n-i} \sum \limits_{j=0}^i \dbinom{i}{j}g(j)\\&= \sum \limits_{i=0}^n \sum \limits_{j=0}^i\dbinom{n}{i}\dbinom{i}{j}(-1)^{n-i}g(j)\\&= \sum \limits_{i=0}^n\sum \limits_{j=0}^i \dbinom{n}{j}\dbinom{n-j}{i-j}(-1)^{n-i}g(j)\\&=\sum \limits_{j=0}^n \dbinom{n}{j}g(j)\sum \limits_{i=j}^n \dbinom{n-j}{i-j}(-1)^{n-i}\\&=\sum \limits_{j=0}^n \dbinom{n}{j}g(j)\sum \limits_{i=0}^{n-j} \dbinom{n-j}{i}(-1)^{n-i-j}\\&=\sum \limits_{j=0}^n \dbinom{n}{j}g(j)\times 0^{n-j}\\&= g(n)\end{aligned} \]

其中用到的等式：

\[\dbinom{n}{m}\dbinom{m}{k} =\dbinom{n}{k}\dbinom{n-k}{m-k} \]

证明：从定义出发，这个等式可以理解为：从 \(n\) 个物品中选 \(m\) 个，再从 \(m\) 个中选 \(k\) 个的方案数，就相当于先从 \(n\) 个数中选出 \(k\) 个，再从剩下的数中选 \(n-k\) 个数的方案。

\[\sum \limits_{i=0}^{n}(-1)^i\dbinom{n}{i}=[n=0] \]

证明：从二项式定理出发，构造 \((1-1)^n\)。

\[\begin{aligned} (1-1)^n&=\sum \limits_{i=0}^{n}\dbinom{n}{i}1^{n-i}\times (-1)^i \\ &=\sum \limits _{i=0}^{n}(-1)^i\dbinom{n}{i} \end{aligned} \]

---

回到这题，我们已经有了 \(f\) 和 \(g\) 之间的关系，这时我们发现 \(g\) 其实就是我们第一问的结果 \(m^n\)。因此 \(f(n,m)=\sum \limits _{i=0}^m \dbinom{m}{i} (-1)^{m-i}i^n\)

线筛出所有的 \(i^n\)，时间复杂度 \(O(n)\)。

球之间互不相同，盒子全部相同

这里引入第二类斯特林数。

定义：\(\begin{Bmatrix}n\\ k\end{Bmatrix}\)，表示将 n 个两两不同的元素，划分为 k 个互不区分的非空子集的方案数。

因此我们枚举有多少个盒子有小球，答案即为 \(ans = \sum \limits _{i=0}^m \begin{Bmatrix}n\\ i\end{Bmatrix}\)。

我们发现上一问中 \(f\) 和斯特林数的区别就是上一问的 \(f\) 中盒子是不同的，因此我们可以考虑将盒子的排列除去。

因此我们可以得到：

\[\begin{aligned}\begin{Bmatrix}n\\ m\end{Bmatrix}&=\frac{1}{m!}f(n,m)\\&=\frac{1}{m!}\sum \limits_{i=0}^m \dbinom{m}{i}(-1)^{m-i}i^n\\&=\frac{1}{m!}\sum \limits_{i=0}^m \frac{m!}{i!(m-i)!} (-1)^{m-i}i^n\\&=\sum \limits_{i=0}^m \frac{(-1)^{m-i}i^n}{i!(m-i)!}\\\end{aligned} \]

我们可以把 \(i\) 项和 \(m-i\) 项分开：

\[\begin{aligned} \begin{Bmatrix}n\\ m\end{Bmatrix}&=\sum \limits_{i=0}^m \frac{(-1)^{m-i}i^n}{i!(m-i)!}\\ &=\sum \limits_{i=0}^m \frac{(-1)^{m-i}}{(m-i)!}\frac{i^n}{i!} \end{aligned} \]

我们设多项式 \(A(x)=\sum \limits _{i=0}^m \frac{i^n}{i!}\)，多项式 \(B(x)=\sum \limits _{i=0}^m\frac{(-1)^{i}}{i!}\)，于是我们不难发现 \(\begin{Bmatrix}n\\ i\end{Bmatrix}=c_i=\sum \limits _{j=0}^ia_ib_{i-j}\)。NTT 卷一下就能得出斯特林数 \(1\sim n\) 项。时间复杂度 \(O(n\log n)\)。

球之间互不相同，盒子全部相同，每个盒子至多装一个球

当球数大于盒子数时，有 \(0\) 种方案。

当球数小于盒子数时，因为盒子都相同，则有 \(1\) 种方案。

球之间互不相同，盒子全部相同，每个盒子至少装一个球

斯特林数定义，求出 \(\begin{Bmatrix}n\\ m\end{Bmatrix}\) 即可。

球全部相同，盒子之间互不相同

运用插板法，把小球排成一列，向小球的 \(n-1\) 个空隙中插入 \(m-1\) 个板，板与板之间即为该盒子中的小球数。

但是这种方法只能适用于每个盒子中都有小球的情况，当可以为空时，我们可以加入 \(m\) 个虚拟小球，这样在插板的时候，我们将板与板之间的小球中一个变为虚拟小球，也就是这个盒子中真实的小球数为小球数减去一。这样我们就可以得出答案 \(\dbinom{m-1}{n+m-1}\)。

球全部相同，盒子之间互不相同，每个盒子至多装一个球

考虑哪个盒子放了球，答案即为 \(\dbinom{m}{n}\)。

球全部相同，盒子之间互不相同，每个盒子至少装一个球

和第 \(7\) 种情况的一开始思考相同，插板，但是没有虚拟小球，答案为 \(\dbinom{m-1}{n-1}\)

球全部相同，盒子全部相同

它 来 了

既然盒子全部相同，那么我们可以把盒子按小球数排个序，这样得到的序列不同时才算不同的方案。

我们可以把这个模型放到二维坐标系上：

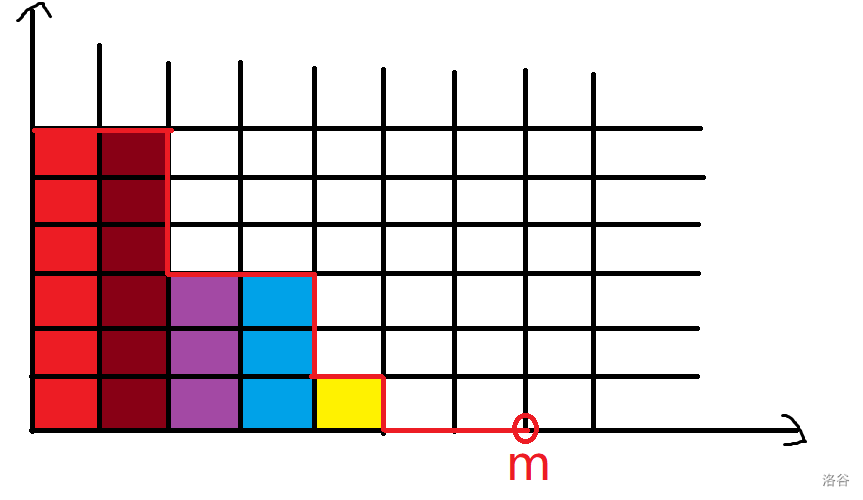
这样我们就可以把问题转化为：从 \((m, 0)\) 开始走，每次只能向上走或向左走，最后走到 \(y\) 轴且与坐标轴所成图形的面积为 \(n\) 的方案数。

设 \(f(n, m)\) 为从 \((m, 0)\) 走到 \(y\) 轴，围成面积为 \(n\) 的方案数，也等同于 \(n\) 个相同小球放入 \(m\) 个相同盒子的方案数。

我们在每个点有两种选择：向左走和向上走。当向左走时，问题转化为计算 \(f(n, m-1)\)，向上走时，填充了 \(m\) 个格子，问题转化为求 \(f(n-m, m)\)。因此我们可以得到递推公式：

\[f(n, m) = f(n, m-1) + f(n - m, m) \]

考虑加速计算这个式子，考虑生成函数。

设 \(F_m(x) =\sum \limits_{i=0}f(i,m)x^i\)，就可以得到：

\[\begin{aligned} F_m(x)&=\sum \limits_{i=0}f(i,m)x^i \\ &=\sum \limits_{i=0}(f(i, m-1) + f(i-m,m))x^i\\ &= F_{m-1}(x)+x^mF_m(x) \end{aligned} \]

解方程即可得到递推公式：\(F_m(x)=\frac{1}{1-x^m}F_{m-1}(x)\)。

因为 \(f(n, 0)=[n=0]\)，所以 \(F_0(x)=1\)。于是就可以得出：

\[F_m(x)=\prod_{i=1}^{m} \frac{1}{1-x^i} \]

两边同时取对数：

\[\begin{aligned} \ln F_m(x)&=\sum_{i=1}^{m}\ln \frac{1}{1-x^i}\\ &=-\sum_{i=1}^{m}\ln(1-x^i) \end{aligned} \]

有一个结论：

\[\ln (1-x^t)=-\sum_{i=1}\frac{x^{ti}}{i} \]

---

证明（感谢 grp 的帮助）：

对式子先求导再积分

\[\ln (1-x^t)=\int \frac{-tx^{t-1}}{1-x^t} \]

（等比数列求和）

\[\sum \limits _{i=0}x^{ti-1}=\frac{1}{1-x^t}\frac{1}{x} \]

提出一个 \(x^t\)。

\[\sum \limits _{i=1}x^{ti-1}=\frac{1}{1-x^t}x^{t-1} \]

再带回一开始的式子：

\[\begin{aligned} \ln (1-x^t) &= \int \frac{-tx^{t-1}}{1-x^t} dx\\ &=\int (-t\sum_{i=1}x^{ti-1})dx\\ &= -\sum_{i=1}\frac{x^{ti}}{i} \end{aligned} \]

---

于是我们就可以化简为

\[\ln F_m(x)=\sum_{i=1}^m\sum_{j=1}\frac{x^{ij}}{j} \]

因为我们只要求前 \(n-1\) 项，所以我们可以枚举 \(i\)，在枚举 \(j\) 一直到 \(ij>n\) 为止，同时向每一项累加系数。这样就可以解决第十问了！

球全部相同，盒子全部相同，每个盒子至多装一个球

来搞笑的，只有 \(0\) 或 \(1\) 两种情况。

球全部相同，盒子全部相同，每个盒子至少装一个球

和第十问类似，只是要求在 \((m, 0)\) 时第一步必须向上走，因此答案即为 \(f(n-m,m)\)。

完整代码（卡了好久的常）：

#define LOCAL
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef pair<int, int> PII;
#define int long long

const int N = 2e6 + 10, P = 998244353, G = 3, Gi = 332748118;
int n, m;
ll fact[N], invfact[N];
int primes[N], cnt;
bool st[N];
ll mi[N];
ll invv[N];
int rev[N], A[N], B[N], S[N];
int lim = 1, len;

inline int qmi(int a, int k, int p)
{
    int res = 1;
    while(k)
    {
        if(k & 1) res = (ll)res * a % p;
        a = (ll)a * a % p;
        k >>= 1;
    }
    return res;
}

inline void init()
{
    mi[1] = 1;
    for(int i = 2; i <= N - 5; i ++ )
    {
        if(!st[i])
        {
            primes[++ cnt] = i;
            mi[i] = qmi(i, n, P);
        }
        for(int j = 1; primes[j] <= (N - 5) / i; j ++ )
        {
            st[primes[j] * i] = true;
            mi[primes[j] * i] = (ll)mi[primes[j]] * mi[i] % P;
            if(i % primes[j] == 0) break;
        }
    }
    invv[1] = 1;
    for(int i = 2; i < N - 5; i ++ ) 
        invv[i] = (ll)(P - P / i) * invv[P % i] % P;
}

inline void NTT(int a[], int opt)
{
    for(int i = 0; i < lim; i ++ )
        if(i < rev[i])
            swap(a[i], a[rev[i]]);
    int up = log2(lim);
    for(int dep = 1; dep <= up; dep ++ )
    {
        int m = 1 << dep;
        int gn;
        if(opt == 1) gn = qmi(G, (P - 1) / m, P);
        else gn = qmi(Gi, (P - 1) / m, P);
        for(int k = 0; k < lim; k += m)
        {
            int g = 1;
            for(int j = 0; j < m / 2; j ++ )
            {
                int t = (ll)a[j + k + m / 2] * g % P;
                int u = a[j + k];
                a[j + k] = ((ll)t + u) % P;
                a[j + k + m / 2] = ((ll)u - t + P) % P;
                g = (ll)g * gn % P; 
            }
        }
    }
    if(opt == -1)
    {
        ll inv = qmi(lim, P - 2, P);
        for(int i = 0; i < lim; i ++ ) a[i] = (ll)a[i] * inv % P;
    }
}

inline void NTT(int a[], int lim, int opt)
{
    for(int i = 0; i < lim; i ++ )
        if(i < rev[i])
            swap(a[i], a[rev[i]]);
    int up = log2(lim);
    for(int dep = 1; dep <= up; dep ++ )
    {
        int m = 1 << dep;
        int gn;
        if(opt == 1) gn = qmi(G, (P - 1) / m, P);
        else gn = qmi(Gi, (P - 1) / m, P);
        for(int k = 0; k < lim; k += m)
        {
            int g = 1;
            for(int j = 0; j < m / 2; j ++ )
            {
                int t = (ll)a[j + k + m / 2] * g % P;
                int u = a[j + k];
                a[j + k] = ((ll)t + u) % P;
                a[j + k + m / 2] = ((ll)u - t + P) % P;
                g = (ll)g * gn % P; 
            }
        }
    }
    if(opt == -1)
    {
        ll inv = qmi(lim, P - 2, P);
        for(int i = 0; i < lim; i ++ ) a[i] = (ll)a[i] * inv % P;
    }
}


inline ll C(int n, int m)
{
    if(m > n) return 0;
    return (ll)fact[n] * invfact[m] % P * invfact[n - m] % P;
}

inline void strlin()
{
    for(int i = 0; i <= n; i ++ ) 
    {
        A[i] = (ll)mi[i] * invfact[i] % P;
        B[i] = (qmi(-1, i, P) * (ll)invfact[i] + P) % P;
    }

    while(lim <= (n + 1) * 2) lim <<= 1, len ++;
    for(int i = 0; i < lim; i ++ )
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));
    
    NTT(A, 1), NTT(B, 1);
    for(int i = 0; i < lim; i ++ ) S[i] = (ll)A[i] * B[i] % P;
    NTT(S, -1); 
}

inline void calc(int lim, int len)
{
    for(int i = 0; i < lim; i ++ )
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));
}

int X[N], Y[N];
inline void mul(int a[], int b[], int to[], int n, int m)
{
    int lim = 1, len = 0;
    while(lim <= (n + m)) lim <<= 1, len ++;
    calc(lim, len);
    for(int i = (lim >> 1); i <= lim; i ++ ) X[i] = Y[i] = 0;
    for(int i = 0; i < (lim >> 1); i ++ )
        X[i] = a[i] % P, Y[i] = b[i] % P;
    NTT(X, lim, 1), NTT(Y, lim, 1);
    for(int i = 0; i < lim; i ++ ) 
        to[i] = (ll)X[i] * Y[i] % P;
    NTT(to, lim, -1);
}

inline void mul(int a[], int b[], int to[], int lim)
{
    for(int i = (lim >> 1); i <= lim; i ++ ) X[i] = Y[i] = 0;
    for(int i = 0; i < (lim >> 1); i ++ )
        X[i] = a[i] % P, Y[i] = b[i] % P;
    NTT(X, lim, 1), NTT(Y, lim, 1);
    for(int i = 0; i < lim; i ++ ) 
        to[i] = (ll)X[i] * Y[i] % P;
    NTT(to, lim, -1);
}

ll b[2][N];
void inv(ll a[], ll to[], ll n)
{
    int cur = 0;
    b[cur][0] = qmi(a[0], P - 2, P);
    int base = 1, lim = 2, len = 1;
    calc(lim, len);
    while(base <= (n + n))
    {
        cur ^= 1;
        memset(b[cur], 0, sizeof b[cur]);
        for(int i = 0; i < base; i ++ ) b[cur][i] = b[cur ^ 1][i] * 2 % P;
        mul(b[cur ^ 1], b[cur ^ 1], b[cur ^ 1], lim);
        mul(b[cur ^ 1], a, b[cur ^ 1], lim);
        for(int i = 0; i < base; i ++ )
            b[cur][i] = (b[cur][i] - b[cur ^ 1][i] + P) % P;
        base <<= 1, lim <<= 1, len ++;
        calc(lim, len);
    }
    for(int i = 0; i < lim; i ++ ) to[i] = b[cur][i];
}

inline void derivative(int a[], int to[], int n)
{
    for(int i = 0; i < n - 1; i ++ )
        to[i] = (ll)(i + 1) * a[i + 1] % P;
    to[n - 1] = 0;
}

inline void integ(int a[], int to[], int n)
{
    for(int i = 1; i <= n; i ++ )
        to[i] = (ll)qmi(i, P - 2, P) * (ll)a[i - 1] % P;
    to[0] = 0;
}

int d[N], in[N], LN[N], inte[N];
inline void ln(int a[], int to[], int n)
{
    inv(a, in, n);
    derivative(a, d, n);
    mul(d, in, inte, n, n);
    integ(inte, to, n);
}

int c[N], E[N];
inline void exp(int a[], int b[], ll n)
{
    if(n == 1)
    {
        b[0] = 1;
        return;
    }
    exp(a, b, (n + 1) >> 1);
    ln(b, LN, n);
    int lim = 1;
    while(lim <= n + n) lim <<= 1;
    for(int i = 0; i < n; i ++ ) c[i] = ((ll)a[i] - LN[i] + P) % P;
    for(int i = n; i < lim; i ++ ) LN[i] = c[i] = 0;
    c[0] ++;
    mul(c, b, b, n, n);
    for(int i = n; i < lim; i ++ ) b[i] = 0;
}

int LNN[N], F[N];

inline ll solve1()
{
    return qmi(m, n, P);
}

inline ll solve2()
{
    if(n > m) return 0;
    return (ll)fact[m] * invfact[m - n] % P;
}

inline ll solve3()
{
    if(n < m) return 0;
    ll res = 0;
    for(int i = 0; i <= m; i ++ )
        if((m - i) & 1) res = ((ll)res - C(m, i) % P * mi[i] % P + P) % P;
        else res = ((ll)res + C(m, i) % P * mi[i] % P) % P;

    return res % P;
}

inline ll solve4()
{
    strlin();
    ll ans = 0;
    for(int i = 0; i <= min(m, n); i ++ ) ans = (ans + S[i]) % P;
    return ans;
}

inline ll solve5()
{
    if(n > m) return 0;
    return 1;
}

inline ll solve6()
{
    if(n < m) return 0;
    return S[m];
}

inline ll solve7()
{
    return C(n + m - 1, m - 1);
}

inline ll solve8()
{
    return C(m, n);
}

inline ll solve9()
{
    if(m > n) return 0;
    return C(n - 1, m - 1);
}

inline ll solve10()
{
    for(int i = 0; i <= n; i ++ ) LNN[i] = F[i] = 0;
    for(int i = 1; i <= m; i ++ )
    {
        for(int j = 1; j <= n / i; j ++ )
            LNN[i * j] = ((ll)LNN[i * j] + invv[j]) % P;
    }
    exp(LNN, F, n + 1);
    return F[n];
}

inline ll solve11()
{
    if(n > m) return 0;
    return 1;
}

inline ll solve12()
{
    if(n < m) return 0;
    return F[n - m];
}

signed main()
{
    double st = clock();

    n = read(), m = read();
    init();
    fact[0] = 1;
    for(int i = 1; i <= n + m; i ++ ) fact[i] = (ll)fact[i - 1] * i % P;
    invfact[n + m] = qmi(fact[n + m], P - 2, P);
    for(int i = n + m; i; i -- )
        invfact[i - 1] = (ll)invfact[i] * i % P;

    cout << solve1() << endl;
    cout << solve2() << endl;
    cout << solve3() << endl;
    cout << solve4() << endl;
    cout << solve5() << endl;
    cout << solve6() << endl;
    cout << solve7() << endl;
    cout << solve8() << endl;
    cout << solve9() << endl;
    cout << solve10() << endl;
    cout << solve11() << endl;
    cout << solve12() << endl;

    return 0;
}