谁说退役就不能接着写学术内容了🤗

学术内容专区，记录一些大悟的东西。

2024.3.27

分子平均动能

先对理想气体做出一些假设：

气体分子与容器壁的碰撞为弹性碰撞，即碰撞前后动量大小不变
气体分子的分布均匀，做不规则运动。体系的温度不会自动降低

设一个气体分子的速度为 $m$ ，速率为 $u$ 。边长为 $L$ 的正方形盒子里有 $N$ 个分子。那么会有 $\frac{N}{3}$ 个分子具有垂直于某一个面方向的动量 $m u$ 。这个分子碰撞到壁后动量变为 $- m u$ 。考虑这个分子碰撞这个容器壁两次的时间间隔围为 $\frac{2 L}{u}$ ，那么连续两次碰撞之间这个分子平均动量变化量即为 $\frac{2 m u}{\frac{2 L}{u}} = \frac{m u^{2}}{L}$ 。

那么 $\frac{N}{3}$ 个分子的动能变化量即为 $\frac{N}{3} \times \frac{m u^{2}}{L}$ 。设容器壁对这些分子的力为 $f$ ，那么动量定理可得 $f = \frac{N}{3} \times \frac{m u^{2}}{L}$ 。

并且 $p = \frac{f}{S} = \frac{f}{L^{2}}$ ，那么 $p V = \frac{N m u^{2}}{3}$ 。

实际所有分子不可能速度全为 $u$ ，设速度为 $u_{i}$ 的分子有 $n_{i}$ 个（ $\sum n_{i} = N$ ），那么对上式修正：

p V = \frac{m}{3} \times (\sum n_{i} u_{i}^{2})

又因为 $\sum n_{i} u_{i}^{2} = N \overset{―}{u_{i}^{2}}$ （其中 $\overset{―}{u_{i}^{2}}$ 为速率平方的平均数），可以得到：

p V = \frac{m N \overset{―}{u_{i}^{2}}}{3} = \frac{2 N}{3} \times \frac{1}{2} m \overset{―}{u_{i}^{2}} = \frac{2 N}{3} \overset{―}{E_{k}}

因此 $p V = \frac{2 N}{3} \overset{―}{E_{k}}$

但是我不会证 $\overset{―}{E_{k}} = \frac{3}{2} k T$ ，wyy 跟我说这个在物竞的统计热力学里有，并且锐评：

统计热力学就是排列组合

反正我不会。

2024.3.26

可逆过程体积功

考虑让压强为 $p$ 的气体在外界压强为 $p_{外} (p_{外} < p)$ 的情况下膨胀。显然气体会对外界做体积功。假设体积从 $V_{1}$ 变为了 $V_{2}$ ，那么对外界做的体积功即为 $p_{外} (V_{2} - V_{1})$ ，于是我们在等压膨胀的情况下对外做的体积功即为对 $p_{外} - V$ 这个图像做积分。

又由于 $p V = n R T$ ，可得 $p = \frac{n R T}{V}$ ，由于 $p_{外} < p$ ，那么我们就让 $p_{外}$ 每次减少一个无穷小量，相应的体积也会增加一个无穷小量。这样的一个过程也可以相当于为一个等压膨胀，可以参考下图：

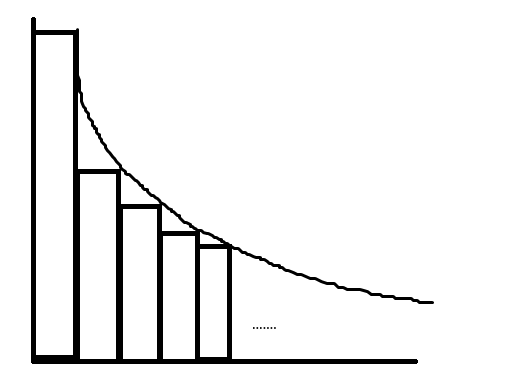
由于减小的是一个无穷小量，因此就相当于对这个图像积分。

写出式子：

W_{体 积} = \int_{V_{1}}^{V_{2}} δ W = \int_{V_{1}}^{V_{2}} p_{外} d V

将 $p_{外} = \frac{n R T}{V}$ 带入可得：

W_{体 积} = \int_{V_{1}}^{V_{2}} n R T \frac{d V}{V} = n R T \ln \frac{V_{2}}{V_{1}}

于是得到了可逆过程的体积功。

2024.3.23

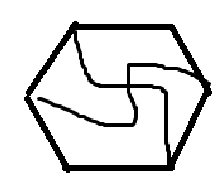
扭曲烷空间结构

首先显然的中间有一个扭船式的环己烷，然后以这个环己烷为基底，可以发现剩下的键是连接了环己烷的对位碳原子的。

因此将其俯视图画出来。形如这个样子

posted @ 2024-03-26 18:01 crimson000 阅读(112) 评论(7) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 闲话7.26——你画我猜特供版

· 闲话1.9

· 气体动理论云云

· 热力学与统计力学

· @物空必能（@tigeduy）的大发现

公告

昵称： crimson000
园龄： 2年3个月
粉丝： 68
关注： 73

+加关注

2025年3月

日

一

二

三

四

五

六

crimsonawa

谁说退役就不能接着写学术内容了🤗

2024.3.27

2024.3.26

2024.3.23

公告

搜索

常用链接

随笔分类

随笔档案

相册

阅读排行榜

评论排行榜

推荐排行榜

最新评论