补码基础

1、演化过程

    假如计算中使用4位的二进制表示数十进制数。最多能表示0-15。如下图，之后牛人做了一个细微的改动，将所有二进制以1开头的数放到0的前面，并且规定用来表示负数-1到-8，这就是4位的补码。

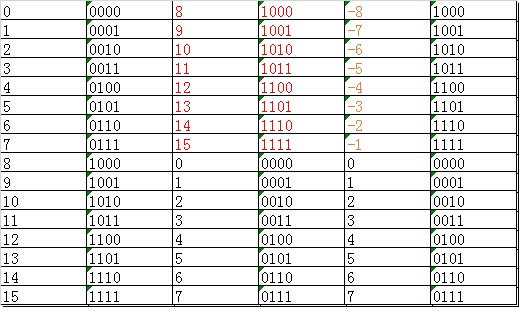
2、这么改动以后，会产生很多有趣的规律。这种规律当然是归纳出来的。

             -1（1111）+1（0001）=0（10000）     //让最高位1溢出，保留4个0。那么就是运算的结果

同理       -8（1000）+7（0111）=-1（1111）     //结果也对哦

通过归纳总结得出结论：（一种命题，哥德尔不完备说的是通过公理演绎方法，有些命题是不能演绎出来的。即不能证明他对，也不能证明他错。所以归纳法和实验才需要继续进行，要不然的话，当科学足够丰富，一切都可以演绎出来了，不需要实验发现新的正确的命题了。公理化方法，所有的定理都能通过公理逻辑演绎出来；演绎出来的定理，不能自相矛盾，即不能演绎出A，又能演绎出A的否命题。无穷小，无穷大。潜无限和实有限。这说的是两种不同的观点。潜无限指一种过程，比如无穷小，到底多少是无穷小，这对应的比喻有“一条直线由无穷多个点组成”，“极限理念”，“一尺之棰，日取其半，万世不竭”。实无限指的是一个对象。比如直线，虽然直线可以理解为无穷多个点，但是向外就是一条有长度的直线段。无穷小和波粒二象性一样，即是零也不是零。它是变化的量。因为有了无穷小，无穷大，数学上才产生了微积分。对于这两种理念。亚里士多德最先提出的哦。引入分析学，就分为标准分析（潜无限）和非标准分析（实无限）。）

           在这个0-15,4位封闭运算中，10进制加减乘除的结果和对应二进制加减乘除的运算是对应的。表明这种设计是非常合理。简直是天才的发现了。

3、给定一正数，如何求对应负数的二进制呢？

          继续归纳法上台： 由于二进制有非常好的对称关系。  0和-1是反的，1和-2,2和-3,....... 

                                 正数2取反就和-3对应，-3+1（0001）就是-2了（2的负数）。

这样，“取反加一”就归纳出来了。 

 4、这是4位的，更高位的8位，16位，32位，64位都有这个规律在。想想看64位可以表示的数字，自然数哦。这些数字的四则运算对计算机来说就好算多了。