软件工程实践2019第三次作业
github地址
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 10 | 10 |
| Estimate | 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | 20 | 20 |
| Analysis | 需求分析 (包括学习新技术) | 60 | 65 |
| Design Spec | 生成设计文档 | 10 | 10 |
| Design Review | 设计复审 | 5 | 5 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| Design | 具体设计 | 10 | 10 |
| Coding | 具体编码 | 60 | 60 |
| Code Review | 代码复审 | 10 | 10 |
| Test | 测试(自我测试,修改代码,提交修改) | 60 | 60 |
| Reporting | 报告 | 10 | 10 |
| Test Repor | 测试报告 | 20 | 20 |
| Size Measurement | 计算工作量 | 20 | 20 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 20 | 20 |
| 合计 | 335 | 340 |
流程
看到题目就知道这一定是一个经典的题目,想了一下感觉除了一些优化剪枝,也想不到什么特别优秀的解法。查了一下发现有一道oj题是解16阶数独的,知道了可以用精确覆盖解决这个问题,用DLX来求解,X算法也只是一个搜索,本质上还是回溯法,巧妙的是DL,DL是指舞蹈链,可以快速的状态转移和恢复,并且每次都能去掉大量的无用状态,因此虽然是搜索,但是利用舞蹈链,速度奇快无比,16阶数独也没什么压力。最后花了一些时间学了一下精确覆盖,发现解决数独就是一个精确覆盖的基础应用,剩下的工作就只剩下写DLX的板子了。
测试
在网上找到几题oj题目,因此最后的测试就用这些题目来测试,最后的代码都能正确快速的通过这些题目。
还有一个9阶的比较难的数据
8 0 0 0 0 0 0 0 0
0 0 3 6 0 0 0 0 0
0 7 0 0 9 0 2 0 0
0 5 0 0 0 7 0 0 0
0 0 0 0 4 5 7 0 0
0 0 0 1 0 0 0 3 0
0 0 1 0 0 0 0 6 8
0 0 8 5 0 0 0 1 0
0 9 0 0 0 0 4 0 0
8 1 2 7 5 3 6 4 9
9 4 3 6 8 2 1 7 5
6 7 5 4 9 1 2 8 3
1 5 4 2 3 7 8 9 6
3 6 9 8 4 5 7 2 1
2 8 7 1 6 9 5 3 4
5 2 1 9 7 4 3 6 8
4 3 8 5 2 6 9 1 7
7 9 6 3 1 8 4 5 2
DLX
精确覆盖
有r个集合\(s_1,s_2,...,s_c\) ,要求选出x 个集合,使得他们的并集是{1,2,3,4,...,n} , 并且这些集合相交为空集。
用一个r行n列的矩阵A来表示,\(A_{ij}=1\) 表示第i个集合中存在元素j 。例如\(n=6,r=5\) 的时候。$s_1=\lbrace1,3\rbrace,s_2=\lbrace2,5\rbrace,s_3=\lbrace4,6\rbrace,s_4=\lbrace3,5,6\rbrace,s_5=\lbrace2,4\rbrace $ ,\(A=
\left[
\begin{matrix}
1 & 0 & 1 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & 1 & 0 & 1\\ 0 & 0 & 1 & 0 & 1 & 1 \\0 & 1 & 0 & 1 & 0 & 0
\end{matrix}
\right]\)
那么精确覆盖则就是从矩阵中选取若干行,组成一个新的矩阵,满足每一列都有且仅有一个1。
X算法
采用X算法,本质上则就是搜索回溯,每次选择一列还没有被覆盖的,选择一行覆盖它,因为每一列只能有一个1,那么可以删除其他这一列出现1的行,同时选择了这一行,可能会同时覆盖了好几列,因此只要在这几列有出现1的行都可以删掉,然后继续搜索下去,回溯的时候恢复即可。
比如上述样例,一开始6列都未被覆盖,我们先覆盖第一列,看到\(s_1\) 在第一列有1,因此我们可以先选择第一行,因此第三列也被覆盖了,因此其他行只要在第一类和第三列出现1都是不可以的,我们可以对应删掉第4行,此时未覆盖的列剩下2,4,5,6,剩下2,3,5行,接下去选择覆盖第2列,第二行刚好在第二列有个1,同时还覆盖了第五列,接着开始删除,第四行在第二列也有一个1,因此选择第二行的话第四行一定不能选,把第四行删掉,此时剩下4,6列没覆盖,行剩下第3行,选择第三行,恰好覆盖了第3、6列,此时所有列都被唯一覆盖,因此找到答案即为第1,2,3行,对应集合\(s_1,s_2,s_3\) 。
DL(舞蹈链)
可以看成一个十字交叉链表,即连接四个方向。对于矩阵中的每一个1,看作一个节点,十字交叉就是上下左右四个放下,每个节点连接着与它同一行的左边一个节点,右边一个节点,与它同一列的上一个节点,下一个节点。
(找了一个网图) 图中每个点就是矩阵中为1的点(点上的数字只是实现代码的时候给的编号)
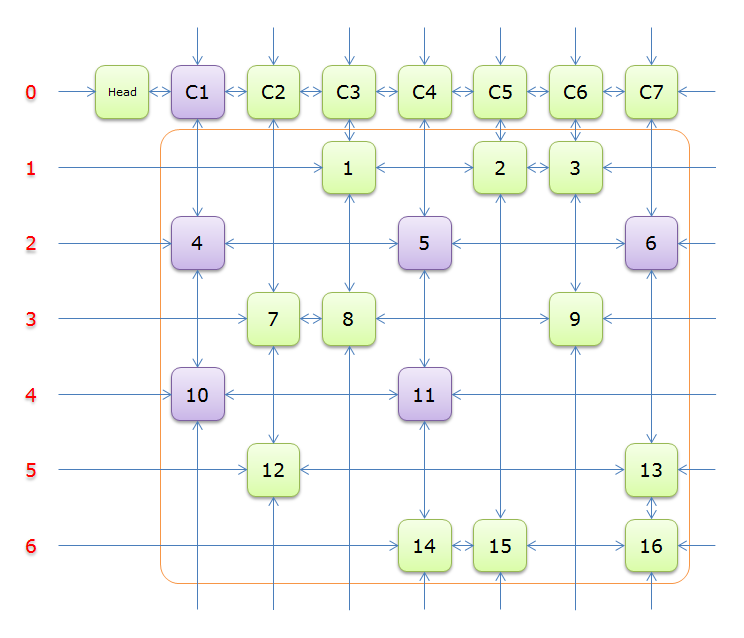
此时我们再看一下X算法,每次要做的是覆盖某一列,然后选择一行覆盖它,删掉与这行有相同列的1的那些行,然后搜索,回溯的时候恢复。用DL就可以快速的删除和恢复。假设对于某一个节点C,我们要删除它,只需要像链表删除那样,(C.L).R=C.R,(C.R).L=C.L ,可以O(1)删除一个节点,再则就是恢复,我们可以看到,虽然我们把C删掉了,只是等效于跳过它,我们恢复这个点只需要(C.L).R=C,(C.R).L=C,就恢复了这个节点,因此我们搜索的时候整行整列的删除也是同一个方法的删除,恢复也是如此。虽然算法的本质还是一样的,但是通过DL我们删除状态,去除无效状态,恢复状态就是极高的效率,精确覆盖的限制性也很强,因此最后搜索的状态也比较有限,DLX能快速的找出答案。
如何解数独
以9*9数独为例子,每一行每一列每一宫1-9都只能出现一次,并且每一个格子都要出现数字。四个限制条件,每个我们用81列来表示,转成一个324列的矩阵求解精确覆盖。
1.每个格子都要有数字
1-81列,表示81个格子中是否填入数字,比如第二行第三列有数字,那么就是改行第\(2*9+3=21\)列为1。
2.每一行都要出现1-9
82-162列。每九列就表示数独中的一行是否出现1-9,比如第四行第五列为1,那么该集合对应的行的第81+3*9+1=109列上为1。
3.每一列都要出现1-9
163-243列。每九列就表示数独中的一列是否出现1-9,比如第三行第六列为5,那么该集合对应的行的第162+5*9+5=212列上为1。
3.每一宫都要出现1-9
244-324列。每九列就表示数独中的一宫是否出现1-9,比如第三行第五列为7,他是第二宫,那么第243+1*9+7=259列为1。
那么我们从1-81个格子逐一转化成集合,如果某个格子有数字那么转成一行,比如第二行第三列有个数字2,
那么他对应的集合是第(2-1)*9+3=12列(第二行第三列填入数字),第(2-1)*9+2+81=82列(第二行填入数字2),第(3-1)*9+2+162=182列(第三列填入数字2),第(1-1)*9+2+243=255列(第一宫填入数字2),这四列为1,其他列为0;如果这一个格子为0,那么说明他有9种可能,可以填1-9,那么枚举1-9,每个数字如上面一样转成一个集合,共九个集合。对每个格子逐一操作,最后求解精确覆盖即可解决问题。
代码
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
typedef pair<int, int>pii;
typedef vector<int>vi;
#define rep(i,a,b) for(int i=(a);i<(b);i++)
#define fi first
#define se second
#define de(x) cout<<#x<<"="<<x<<endl;
#define dd(x) cout<<#x<<"="<<x<<" " ;
#define pb(x) push_back(x)
#define sz(x) (int)x.size()
#define lowbit(a) ((a)&-(a))
#define per(i,a,b) for(int i=(b)-1;i>=(a);--i)
const int N = 1e5 + 5;
const int M = 1e3 + 5;
int m;
int mat[M][M];
struct DLX {
int U[N], D[N], L[N], R[N], col[N], val[N], num[N];
int cnt;
int len;
vi ans;
void init(int _len) {
len = _len;
rep(i, 0, len + 1)U[i] = D[i] = L[i] = R[i] = col[i] = val[i] = num[i] = 0;
ans.clear();
rep(i, 0, len + 1) {
U[i] = i, D[i] = i, L[i] = i - 1, R[i] = i + 1;
col[i] = i;
}
L[0] = len, R[len] = 0;
cnt = len;
}
void add(int ss, vector<int> ele) {
int now = cnt + 1;
for (int i = 0; i<sz(ele); ++i) {
int v = ele[i];
L[++cnt] = cnt - 1;
R[cnt] = cnt + 1;
U[cnt] = U[v];
D[U[v]] = cnt;
D[cnt] = v;
U[v] = cnt;
col[cnt] = v;
num[v]++;
val[cnt] = ss;
}
L[now] = cnt, R[cnt] = now;
}
void remove(int c) {
R[L[c]] = R[c], L[R[c]] = L[c];
for (int i = D[c]; i != c; i = D[i]) {
for (int j = R[i]; j != i; j = R[j]) {
U[D[j]] = U[j];
D[U[j]] = D[j];
num[col[j]]--;
}
}
}
void restore(int c) {
R[L[c]] = c, L[R[c]] = c;
for (int i = U[c]; i != c; i = U[i])
for (int j = R[i]; j != i; j = R[j]) {
U[D[j]] = j;
D[U[j]] = j;
num[col[j]]++;
}
}
bool dfs() {
if (R[0] == 0)return true;
int c = R[0];
for (int i = R[0]; i != 0; i = R[i]) {
if (num[i]<num[c])
c = i;
}
remove(c);
for (int i = D[c]; i != c; i = D[i]) {
for (int j = R[i]; j != i; j = R[j])
remove(col[j]);
ans.pb(val[i]);
if (dfs())return true;
ans.pop_back();
for (int j = L[i]; j != i; j = L[j])
restore(col[j]);
}
restore(c);
return false;
}
}dlx;
int main(int argc, char **argv)
{
freopen(argv[6], "r", stdin);
freopen(argv[8], "w", stdout);
m = atoi(argv[2]);
int T = atoi(argv[4]);
scanf("%d%d", &m, &T);
while (T--) {
int gr, gc;
bool f = false;
if (m == 6 || m == 8 || m == 4 || m == 9) {
f = true;
if (m == 6)gr = 2, gc = 3;
else if (m == 8)gr = 4, gc = 2;
else gr = gc = sqrt(m);
dlx.init(m*m * 4);
}
else dlx.init(m*m * 3);
rep(i, 1, m + 1) {
rep(j, 1, m + 1) {
scanf("%d", &mat[i][j]);
for (int k = 1; k <= m; ++k)
if (mat[i][j] == 0 || mat[i][j] == k) {
vi t;
t.pb((i - 1)*m + j);
t.pb((i - 1)*m + m*m + k);
t.pb((j - 1)*m + 2 * m*m + k);
if (f)t.pb(((i - 1) / gr*gr + (j - 1) / gc)*m + k + 3 * m*m);
dlx.add((i*m + j)*m + k - 1, t);
}
}
}
dlx.dfs();
for (int i = 0; i<sz(dlx.ans); ++i) {
int v = dlx.ans[i];
int k = v%m;
int r = v / m / m;
int c = (v / m) % m;
if (c == 0)r--, c = m;
mat[r][c] = k + 1;
}
rep(i, 1, m + 1) {
rep(j, 1, m + 1) {
if (j>1)printf(" ");
printf("%d", mat[i][j]);
}
printf("\n");
}
printf("\n");
}
return 0;
}
性能探查
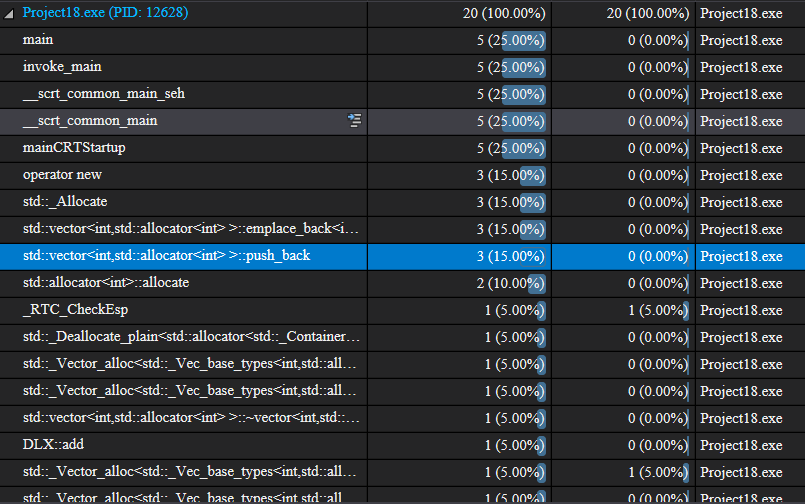


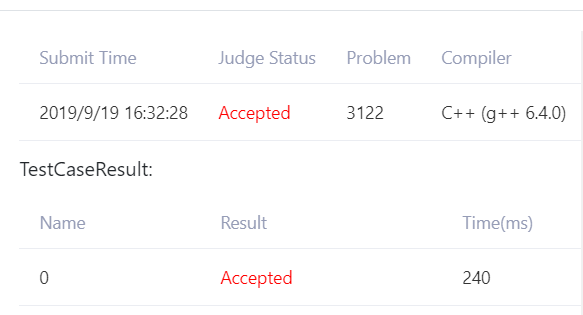

 浙公网安备 33010602011771号
浙公网安备 33010602011771号