【Matlab学习2.5】稀疏矩阵
矩阵的存储方式
完全存储方式：将矩阵的全部元素按列存储。
稀疏存储方式：只存储矩阵的非零元素的值及其位置，即行号和列号。
注意，采用稀疏存储方式时，矩阵元素的存储顺序并没有改变，也是按列的顺序进行存储。
$ A = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 5 & 0 & 0 \\ 2 & 0 & 0 & 7 \\ \end{bmatrix} $
A 矩阵的稀疏存储方式：
（1，1），1
（3，1），2
（2，2），5
（3，4），7
当矩阵的规模很大时，采用稀疏存储方式可以大大节约存储空间。
稀疏存储方式的产生
完全存储方式与稀疏存储方式之间的转化
A=sparse(S)：将矩阵 S 转化为稀疏存储方式的矩阵 A。
S=full(A)：将矩阵 A 转化为完全存储方式的矩阵 S。
例2.5.1：
>> A = sparse(eye(5))
>> B = full(A)
>> whos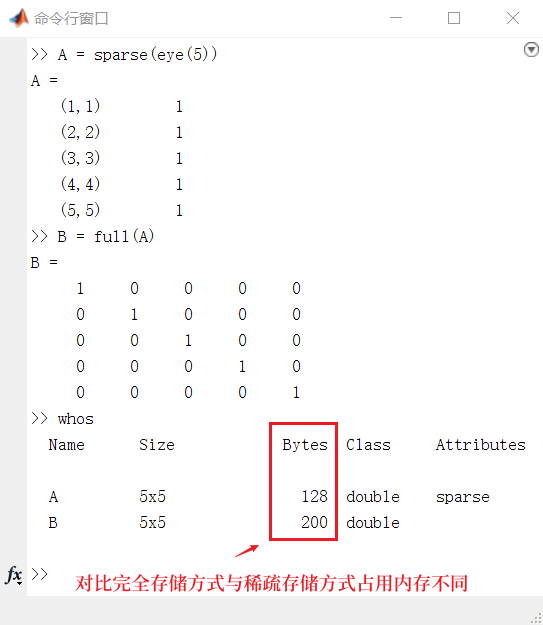
直接建立稀疏存储矩阵
sparse 函数的其他调用格式：
sparse(m,n)：生成一个 m×n 的所有元素都是零的稀疏矩阵。
sparse(u,v,S)：其中 u、v、S 是3个等长的向量。S 是要建立的稀疏存储矩阵的非零元素，u(i)、v(i) 分别是 S(i) 的行和列下标。
例2.5.2：
>> A = sparse([1,2,2],[2,1,4],[4,5,-7])
A =
(2,1) 5
(1,2) 4
(2,4) -7
>> B = full(A)
B =
0 4 0 0
5 0 0 -7使用 spconvert 函数直接建立稀疏存储矩阵：
其调用格式为：B = spconvert (A)
其中，A为一个 m×3 或 m×4 的矩阵，其每行表示一个非零元素，m 是非零元素的个数 。
A(i,1) 表示第 i 个非零元素所在的行；
A(i,2) 表示第 i 个非零元素所在的列；
A(i,3) 表示第 i 个非零元素值的实部；
A(i,4) 表示第 i 个非零元素值的虚部。
若矩阵的全部元素都是实数，则无须第4列。
例2.5.2：
>> A = [2,2,1; 2,1,-1; 2,4,3]
A =
2 2 1
2 1 -1
2 4 3
>> B = spconvert(A)
B =
(2,1) -1
(2,2) 1
(2,4) 3
>> C = [1,2,2,0; 2,1,4,4; 4,5,-7,-3]
C =
1 2 2 0
2 1 4 4
4 5 -7 -3
>> D = spconvert(C)
D =
(2,1) 4.0000 + 4.0000i
(1,2) 2.0000 + 0.0000i
(4,5) -7.0000 - 3.0000i带状稀疏矩阵的稀疏存储
稀疏矩阵有两种基本类型：无规则结构的稀疏矩阵与有规则结构的稀疏矩阵。
带状稀疏矩阵就是一种十分典型的具有规则结构的稀疏矩阵，它是指所有非零元素集中在对角线上的矩阵。
[ B,d ] = spdiags (A)：从带状稀疏矩阵 A 中提取全部非零对角线元素赋给矩阵 B 及其这些非零对角线的位置向量 d。
A = spdiags(B,d,m,n)：产生带状稀疏矩阵的稀疏存储矩阵 A， 其中 m 、n 为原带状稀疏矩阵的行数与列数，矩阵 B 的第 i 列即为原带状稀疏矩阵的第 i 条非零对角线， 向量 d 为原带状稀疏矩阵所有非零对角线的位置。
例2.5.3：
>> A = [11,0,0,12,0,0; 0,21,0,0,22,0; 0,0,31,0,0,32; 41,0,0,42,0,0; 0,51,0,0,52,0]
A =
11 0 0 12 0 0
0 21 0 0 22 0
0 0 31 0 0 32
41 0 0 42 0 0
0 51 0 0 52 0
>> [ B,d ] = spdiags(A)
B =
0 11 12
0 21 22
0 31 32
41 42 0
51 52 0
d =
-3
0
3
%利用带状稀疏矩阵非零对角线元素组成的矩阵 B，以及对角线位置组成的向量 d，命令执行后产生一个稀疏存储矩阵 A。
>> A = spdiags(B,d,5,6)
A =
(1,1) 11
(4,1) 41
(2,2) 21
(5,2) 51
(3,3) 31
(1,4) 12
(4,4) 42
(2,5) 22
(5,5) 52
(3,6) 32总结：
用 spdiags 函数产生带状稀疏矩阵的稀疏存储 A： A = spdiags(B,d,m,n)。
其中，m、n 为原带状矩阵的行数与列数。B 为 r×p 矩阵，这里 r = min(m,n)，p 为原带状矩阵所有非零对角线的条数，矩阵 B 的第 i 列即为原带状矩阵的第 i 条非零对角线。
取值方法是：若非零对角线上元素个数等于 r，则取全部元素；若非零对角线上元素个数小于 r，则应该用零补足到 r 个元素。
补零的原则是：若 m＜n（行数＜列数）， 则 d<0 时（主对角线以下）在后面补 0，d>0 （主对角线以上）时在后面补 0 ；当 m≥n（行数≥列数），则 d<0 时在后面补 0；d>0 时在前面补 0。
单位矩阵的稀疏存储
speye(m,n)返回一个 m×n 的稀疏存储单位矩阵。
例2.5.4：
>> speye(3)
ans =
(1,1) 1
(2,2) 1
(3,3) 1
例2.5.5 稀疏矩阵的应用实例：
求下列三对角线性方程组的解。
$$\left[\begin{array}{ccccc}2 & 3 & & & \\1 & 4 & 1 & & \\& 1 & 6 & 4 & \\& & 2 & 6 & 2 \\& & & 1 & 1\end{array}\right]\left[\begin{array}{c}x_{1} \\x_{2} \\x_{3} \\x_{4} \\x_{5}\end{array}\right]=\left[\begin{array}{c}0 \\3 \\2 \\1 \\5\end{array}\right]$$
>> kf1 = [1; 1; 2; 1; 0];
>> k0 = [2; 4; 6; 6; 1];
>> k1 = [0; 3; 1; 4; 2];
>> B = [kf1,k0,k1];
>> d = [-1; 0; 1];
>> A = spdiags(B,d,5,5);
>> f=[0; 3; 2; 1; 5];
>> x = A\f
x =
-0.1667
0.1111
2.7222
-3.6111
8.6111
注意：当参与运算的数据对象不全是稀疏存储矩阵时，所得结果是完全存储形式。
思考：
1.稀疏矩阵与稀疏存储矩阵有何区别？
2.产生5阶稀疏存储单位矩阵A，使用至少3种方法。
答案：
1.稀疏矩阵是0元素个数多于非0元素个数的矩阵，稀疏矩阵可以采用稀疏存储方式，也可以采用完全存储方式；
稀疏存储矩阵是按照系数存储方式存储的矩阵，稀疏存储矩阵既可以是稀疏矩阵，也可以是稠密矩阵。
2.
%完全存储方式与稀疏存储方式之间的转化，使用 sparse 函数和 eye 函数
>> A = sparse(eye(5))
A =
(1,1) 1
(2,2) 1
(3,3) 1
(4,4) 1
(5,5) 1
%直接建立稀疏存储矩阵，使用 sparse 函数
>> A = sparse ([1,2,3,4,5],[1,2,3,4,5],[1,1,1,1,1])
A =
(1,1) 1
(2,2) 1
(3,3) 1
(4,4) 1
(5,5) 1
%直接建立稀疏存储矩阵，使用 spconvert 函数
>> A = [1,1,1; 2,2,1; 3,3,1; 4,4,1; 5,5,1];
>> spconvert(A)
ans =
(1,1) 1
(2,2) 1
(3,3) 1
(4,4) 1
(5,5) 1
%单位矩阵的稀疏存储，使用 speye 函数
>> A = speye (5,5)
A =
(1,1) 1
(2,2) 1
(3,3) 1
(4,4) 1
(5,5) 1
友链：朋友的博客，第二章总结「matlab学习笔记」MATLAB矩阵处理
