【Matlab学习2.4】矩阵的特征值与特征向量

矩阵特征值的数学定义

设A是n阶方阵，如果存在常数λ和n维非零列向量x，使得等式Ax=λx成立，则称λ为A的特征值，x是对应特征值λ的特征向量。

求矩阵的特征值与特征向量

在Matlab中，计算矩阵的特征值和特征向量的函数是eig，常用的调用格式有两种：

E=eig(A)：求矩阵A的全部特征值，构成向量E。

[X,D]=eig(A)：求矩阵A的全部特征值，构成对角阵D，并产生矩阵X，X各列是相应的特征向量。

例2.4.1：

>> A = [1 1 0; 1 0 5; 1 10 2]
A =
     1     1     0
     1     0     5
     1    10     2
>> [X,D] = eig(A)
X =
    0.0722    0.9751    0.0886
    0.5234   -0.0750   -0.6356
    0.8490   -0.2089    0.7669
D =
    8.2493         0         0
         0    0.9231         0
         0         0   -6.1723
>> A*X(:,1)
ans =
    0.5956
    4.3174
    7.0040
>> D(1)*X(:,1)
ans =
    0.5956
    4.3174
    7.0040

例2.4.2：

设$$ A= \begin{bmatrix} R_{3\times3} & O_{3\times2} \\ O_{2\times3} & S_{2\times2} \\ \end{bmatrix} $$

又设𝝀_𝒊为R的特征值，𝝀_𝒋为S的特征值，𝒙_𝐢 = (𝜶𝟏, 𝜶𝟐, 𝜶𝟑)′ 是R对应于𝝀_𝒊的特征 向量，𝒚_𝐣 = (𝜷_𝟏, 𝜷_𝟐)′是S对应于𝝀_𝒋的特征向量，试验证：

（1）𝝀_𝒊、𝝀_𝒋为A的特征值。

（2）𝐩_𝐢 = (𝜶𝟏, 𝜶𝟐, 𝜶𝟑, 𝟎, 𝟎)′是A对应于𝝀_𝒊的特征向量，𝒒_𝐣 = (𝟎, 𝟎, 𝟎,𝜷𝟏,𝜷𝟐)′是A对应于𝝀_𝒋的特征向量。

>> R = [-1 2 0; 2 -4 1; 1 1 -6];
>> S = [1 2; 2 3];
>> A = [R,zeros(3,2); zeros(2,3),S];
>> [X1,d1] = eig(R)
>> [X2,d2] = eig(S)
>> [X3,d3] = eig(A)

A矩阵的特征值由R矩阵的特征值和S矩阵的特征值组成，关于A矩阵每个特征值的特征向量，前三个特征向量的前三个元素是R的特征向量，后两个特征向量的后两个元素是S的特征向量，运算结果与结论相符。

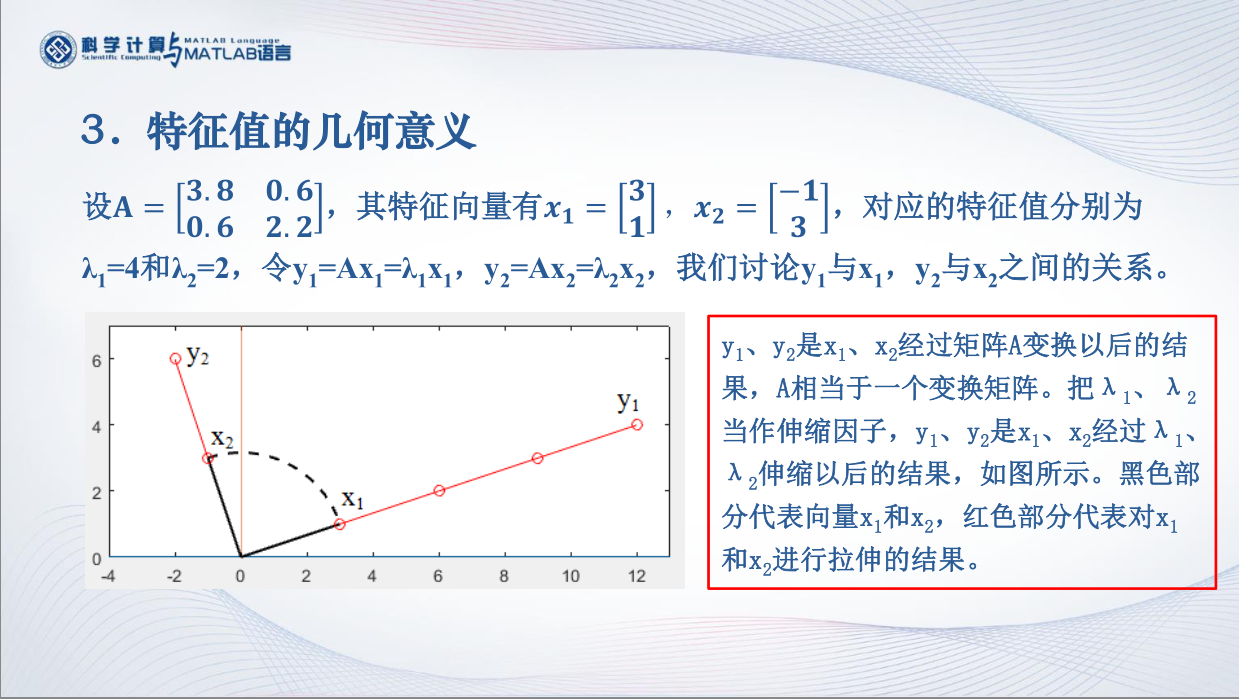
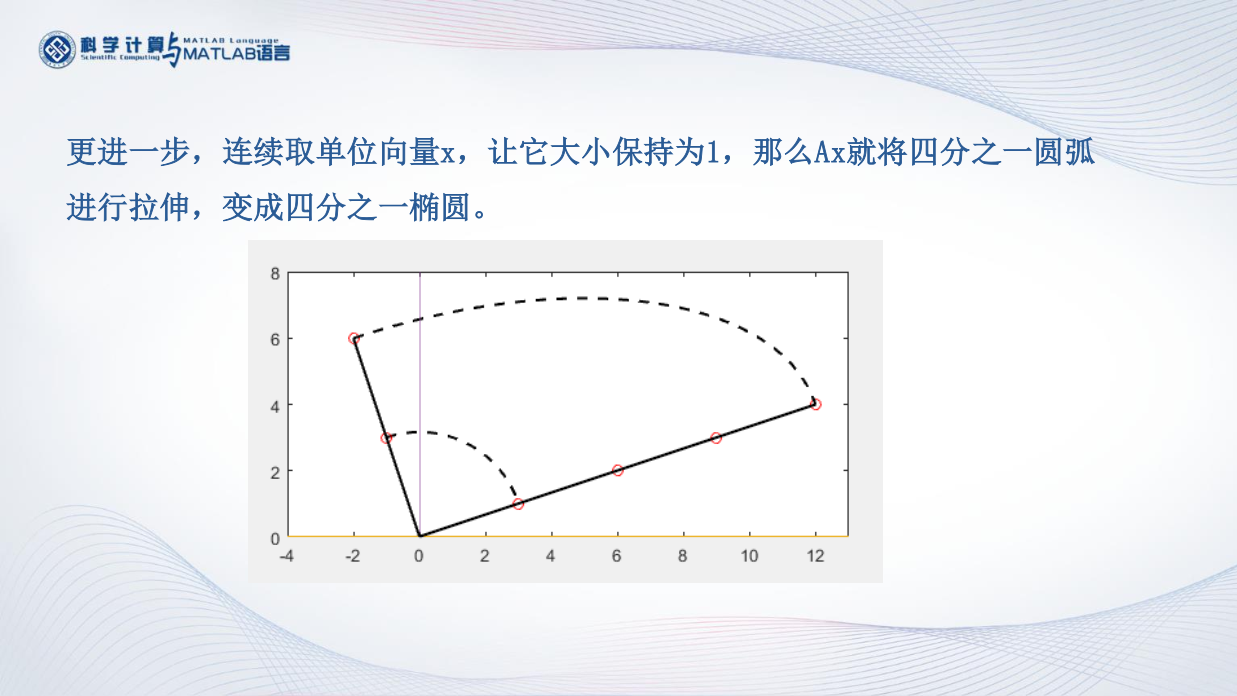
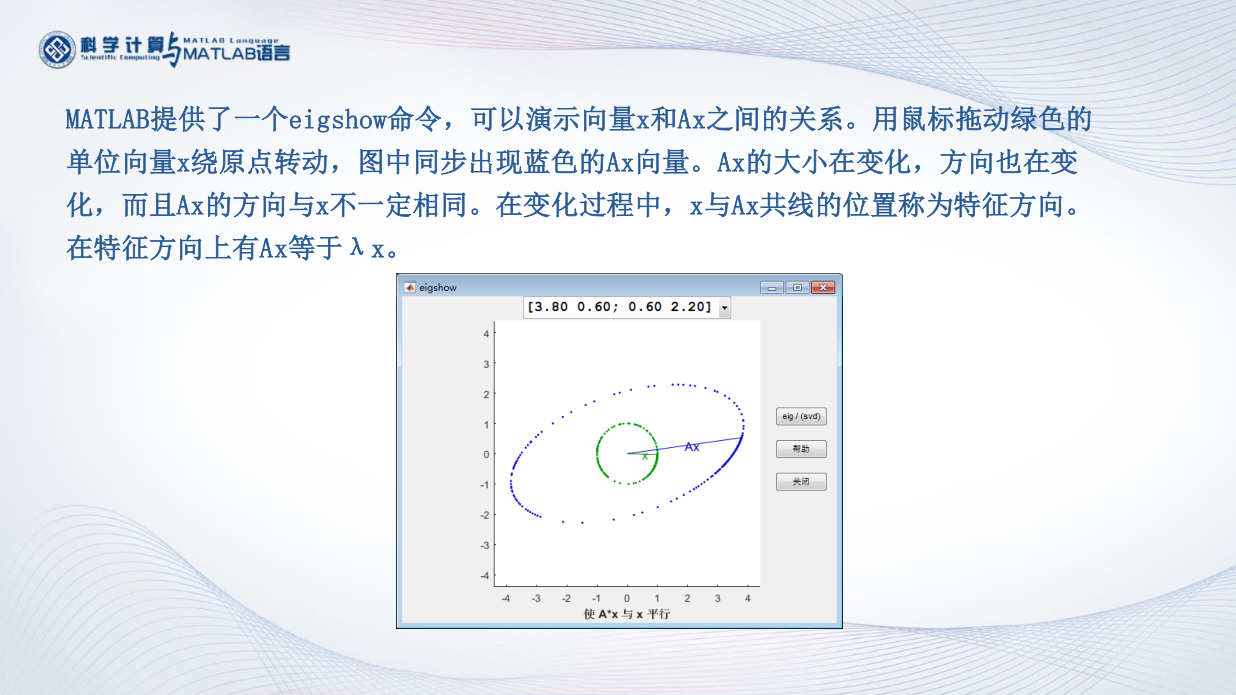
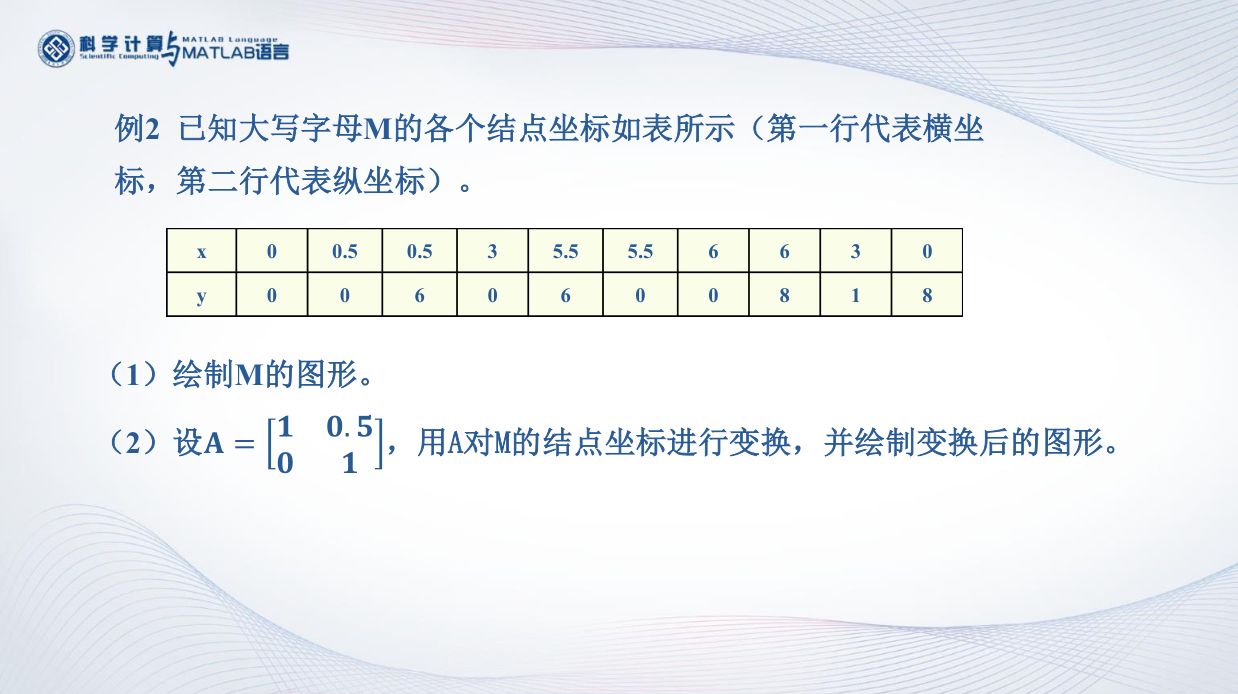
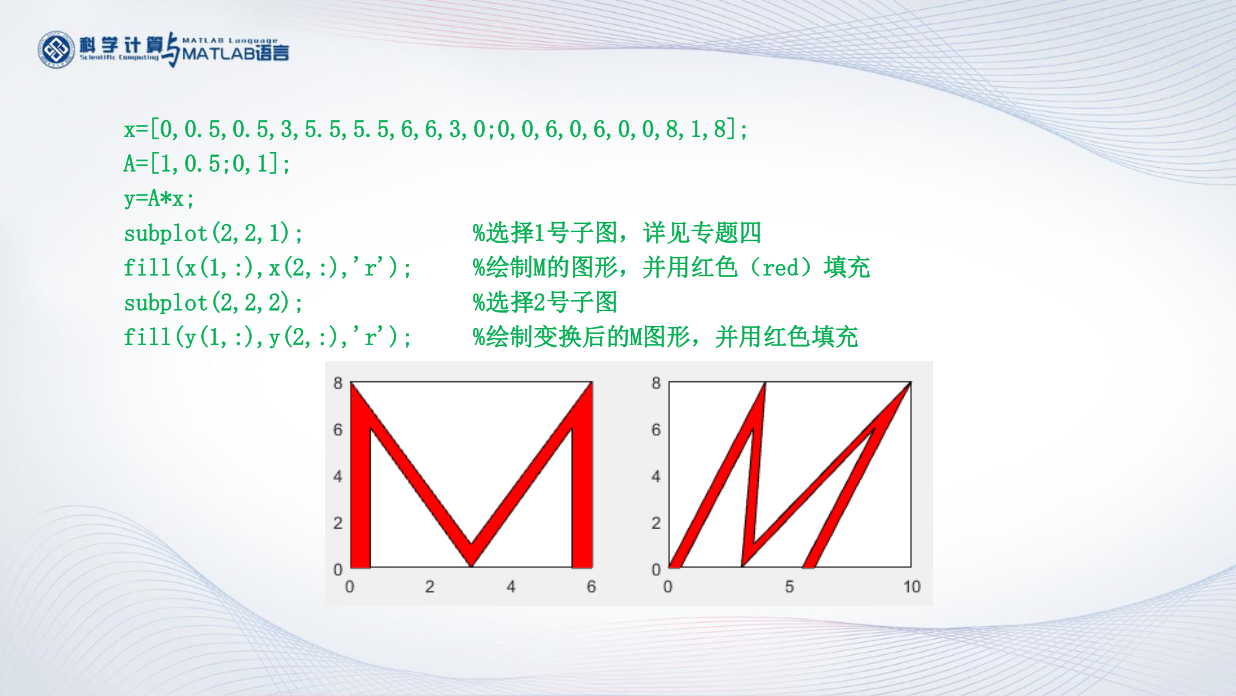
特征值的几何意义 

设 $ A = \begin{bmatrix} 3.8 & 0.6 \\ 0.6 & 2.2 \\ \end{bmatrix} $，其特征向量有 $ x_1 = \begin{bmatrix} 3 \\ 1 \\ \end{bmatrix} $，$ x_2 = \begin{bmatrix} -1 \\ 3 \\ \end{bmatrix} $，对应的特征值分别为 $λ_1=4$ 和 $λ_2=2$，令 $y_1=Ax_1=λ_1x_1$，$y_2=Ax_2=λ_2x_2$，我们讨论$y_1$与$x_1$，$y_2$与$x_2$之间的关系。