【Matlab学习2.3】矩阵求值

方阵的行列式值

把一个方阵看作一个行列式，并对其按行列式的规则求值，这个值就称为所对应的行列式的值。

det(A)：求方阵A所对应的行列式的值。 

例2.3.1：

验证 det(A^-1)=1/det(A)。

>> format rat
>> A = [1 3 2; -3 2 1; 4 1 2]
A =
       1              3              2       
      -3              2              1       
       4              1              2       
>> det(inv(A))
ans =
       1/11    
>> 1/det(A)
ans =
       1/11    

矩阵的秩

矩阵线性无关的行数或列数称为矩阵的秩。

rank(A)：求矩阵A的秩。

例2.3.2：

求 3~20 阶魔方阵的秩。

>> for n = 3:20
r(n) = rank(magic(n));
end
>> bar(r)
>> grid on
>> axis([2,21,0,20])
>> [3:20;r(3:20)]

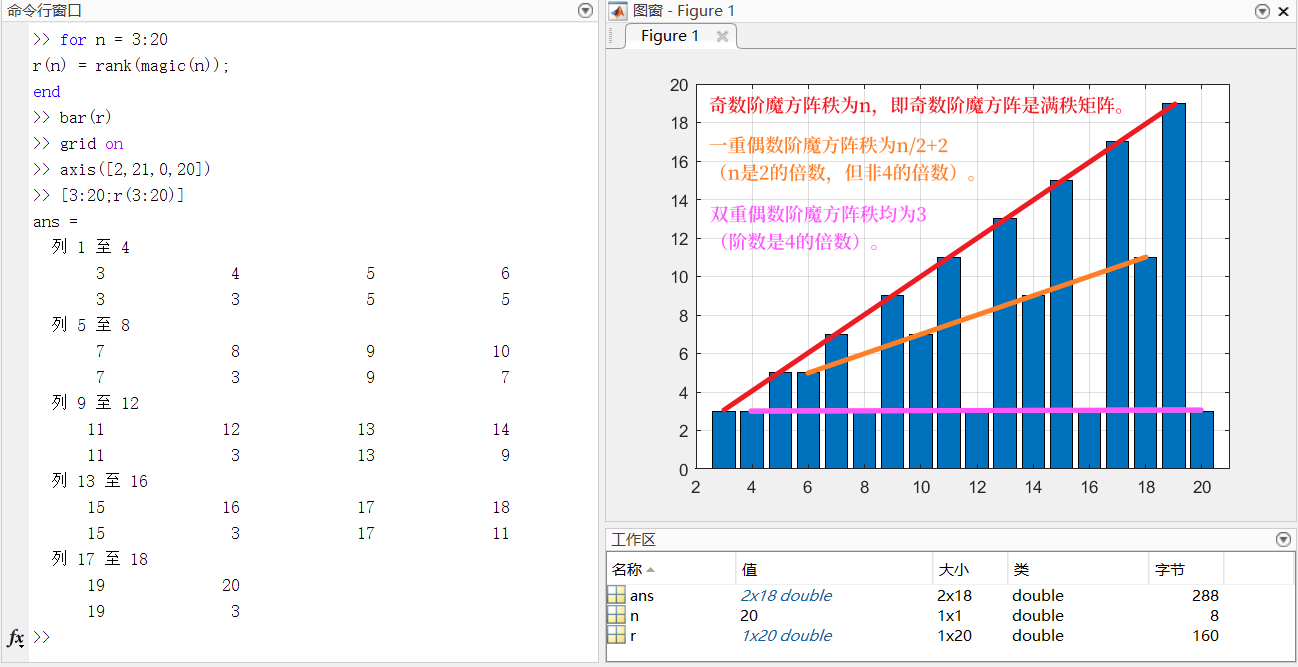
矩阵的迹

矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和。

trace(A)：求矩阵A的迹。

例2.3.3：

>> A=[1,3,2; -3,2,1; 4,1,2]
A =
       1              3              2       
      -3              2              1       
       4              1              2       
>> b = trace(A)
b =
       5       
>> t = sum(diag(A))
t =
       5     

矩阵的范数

矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度。 

向量的3种常用范数

向量 1-范数：向量元素的绝对值之和。

$$ \begin{Vmatrix} V \end{Vmatrix}_1= \sum_{i=1}^n |v_i| $$

向量 2-范数：向量元素绝对值的平方和的平方根。

$$\begin{Vmatrix} V \end{Vmatrix}_2 = \sqrt{\sum_{i=1}^n |v_i|^2}$$

向量 ∞-范数：所有向量元素绝对值中的最大值。

$$\begin{Vmatrix} V \end{Vmatrix}_\infty = \max_{1\leq i\leq n}{\lbrace|v_i|\rbrace}$$

在 Matlab 中，求向量范数的函数为：

norm(V)或norm(V,2)：计算向量 V 的 2-范数。

norm(V,1)：计算向量 V 的 1-范数。

norm(V,inf)：计算向量 V 的 ∞-范数。

矩阵的范数

矩阵 A 的 1-范数：所有矩阵列元素绝对值之和的最大值。

$$\begin{Vmatrix} A \end{Vmatrix}_1 = \max_{1\leq j\leq n}{\lbrace\sum_{i=1}^m|a_{ij}|\rbrace}$$

矩阵 A 的 2-范数：A'A 矩阵的最大特征值的平方根。

$$\begin{Vmatrix} A \end{Vmatrix}_2 = \sqrt{\lambda_1}$$

其中 λ₁ 为 A'A 的最大特征值。

矩阵 A 的 ∞-范数：所有矩阵行元素绝对值之和的最大值。

$$\begin{Vmatrix} A \end{Vmatrix}_\infty = \max_{1\leq i\leq m}{\lbrace\sum_{j=1}^m|a_{ij}|\rbrace}$$

Matlab 提供了求3种矩阵范数的函数，其函数调用格式与求向量的范数的函数完全相同。

例2.3.4：

>> x = [2 0 1; -1 1 0; -3 3 0]
x =
       2              0              1       
      -1              1              0       
      -3              3              0       
>> n = norm(x)
n =
    5909/1251  
>> n = norm(x,1)
n =
       6       

矩阵的条件数

矩阵 A 的条件数等于 A 的范数与 A 的逆矩阵的范数的乘积。

条件数越接近于1，矩阵的性能越好，反之，矩阵的性能越差。

在 Matlab 中，计算矩阵A的3种条件数的函数是：

cond(A,1)：计算 A 的 1-范数下的条件数。

cond(A)或cond(A,2)：计算 A 的 2-范数数下的条件数。

cond(A,inf)：计算 A 的 ∞-范数下的条件数。

例2.3.5：

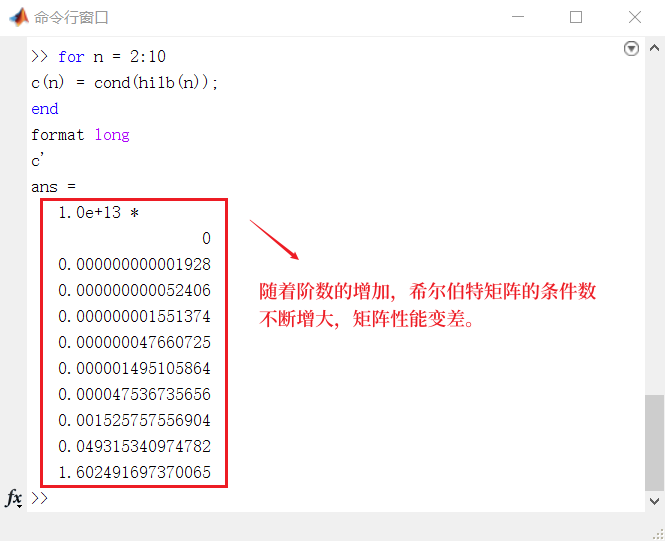
求 2~10 阶希尔伯特矩阵的条件数。

>> for n = 2:10
c(n) = cond(hilb(n));
end
format long
c'