【Matlab学习2.1】特殊矩阵
通用性的特殊矩阵
zeros 函数：产生全0矩阵，即零矩阵。
ones 函数：产生全1矩阵，即幺矩阵。
eye 函数：产生对角线为1的矩阵。当矩阵是方阵时，得到一个单位矩阵。
rand 函数：产生 $(0,1)$ 区间均匀分布的随机矩阵。
randn 函数：产生均值为0，方差为1的标准正态分布随机矩阵。
zeros函数的调用格式
zeros(m)：产生m×m零矩阵。zeros(m,n)：产生m×n零矩阵。zeros(size(A))：产生与矩阵A同样大小的零矩阵。
例2.1.1：
>> A = zeros(2,3)
A =
0 0 0
0 0 0
>> zeros(size(reshape(A,3,2)))
ans =
0 0
0 0
0 0例2.1.2：
首先产生5阶两位随机整数矩阵 A，再产生均值为 0.6、方差为 0.1 的 5 阶正态分布随机矩阵 B，最后验证 $(A+B)I=IA+BI$（$I$ 为单位矩阵）。
提示：
rand 函数：产生(0，1)开区间均匀分布的随机数 x。
fix(a+(b-a+1)*x)：产生 [a，b] 区间上均匀分布的随机整数。
randn 函数：产生均值为 0、方差为 1 的标准正态分布随机数 x。
μ+σx：得到均值为 μ、方差为 σ2 的随机数。
答案：
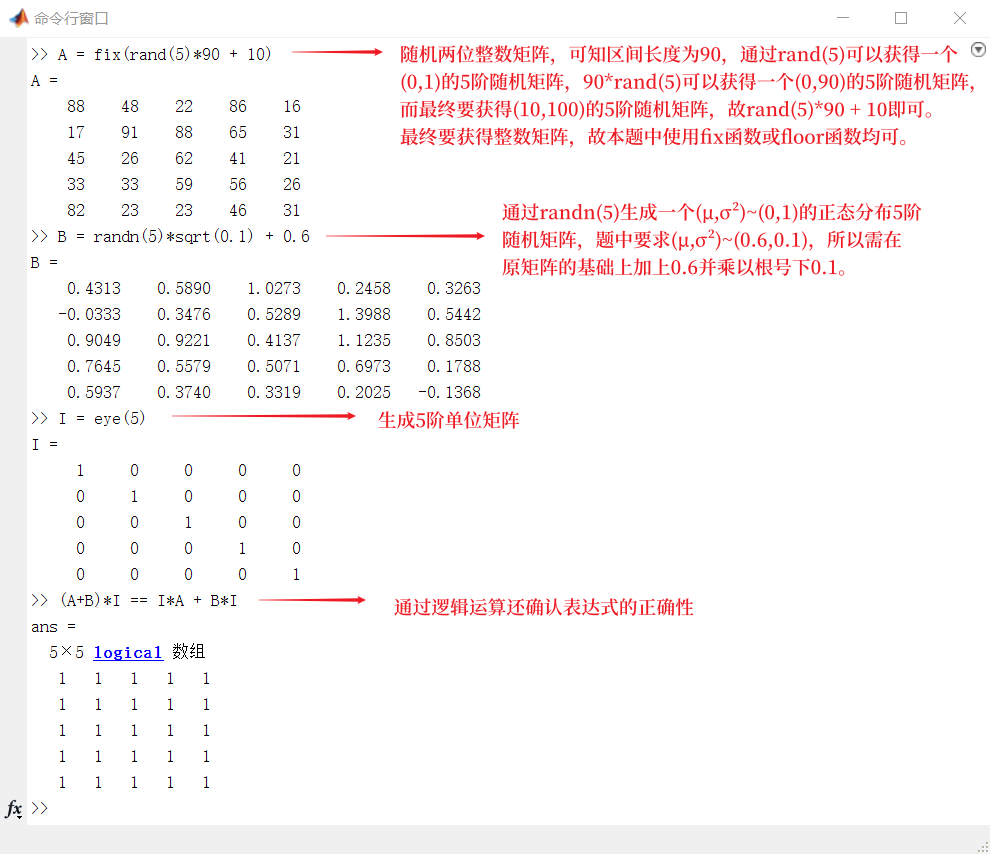
>> A = fix(rand(5)*90 + 10)
>> B = randn(5)*sqrt(0.1) + 0.6
>> I = eye(5)
>> (A+B)*I == I*A + B*I其中，B 矩阵的推导如下：
方法一：期望和方差的性质 $$ \begin{cases} E(aX+b)=aE(x)+b \\ D(aX+b)=a^{2}D(X) \\ \end{cases} $$
设 $X$ 为 randn 函数生成的矩阵，可知 $B=aX+b$。
由题意得方式组 $$ \begin{cases} E(X)=0 \\ D(X)=1 \\ E(aX+b)=aE(X)+b=0.6 \\ D(aX+b)=a^{2}D(X)=0.1 \\ \end{cases} $$
解得 $$ \begin{cases} a=\sqrt{0.1} \\ b=0.6 \\ \end{cases} $$
$B=aX+b=\sqrt{0.1}X+0.6$
方法二：正态分布的性质
详见下图
>> A = fix(rand(5)*90 + 10)
A =
88 48 22 86 16
17 91 88 65 31
45 26 62 41 21
33 33 59 56 26
82 23 23 46 31
>> B = randn(5)*sqrt(0.1) + 0.6
B =
0.4313 0.5890 1.0273 0.2458 0.3263
-0.0333 0.3476 0.5289 1.3988 0.5442
0.9049 0.9221 0.4137 1.1235 0.8503
0.7645 0.5579 0.5071 0.6973 0.1788
0.5937 0.3740 0.3319 0.2025 -0.1368
>> I = eye(5)
I =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
>> (A+B)*I == I*A + B*I
ans =
5×5 logical 数组
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
用于专门学科的特殊矩阵
魔方矩阵——Magic Square
n 阶魔方阵由 1,2,3,…,n2 共 n2 个整数组成，且每行、每列以及主、副对角线上各 n 个元素之和都相等。
n 阶魔方阵每行每列元素的和为 $\cfrac{1+2+3+…+ n^2}{n}$，即 $\cfrac{n+n^3}{2}$。
n>2 时有很多不同的n阶魔方阵，Matlab 函数magic(n)产生一个特定的魔方阵。
例2.1.3：
产生8阶魔方阵，求其每行每列元素的和。
>> M = magic(8)
M =
64 2 3 61 60 6 7 57
9 55 54 12 13 51 50 16
17 47 46 20 21 43 42 24
40 26 27 37 36 30 31 33
32 34 35 29 28 38 39 25
41 23 22 44 45 19 18 48
49 15 14 52 53 11 10 56
8 58 59 5 4 62 63 1
>> sum(M(1,:)) #每行元素的和相同，故只需求出第一行即可
ans =
260
>> sum(M(:,1)) #每列元素的和相同，故只需求出第一列即可
ans =
260范德蒙矩阵
对于向量 $\vec{v}= [v_1，v_2，\ldots，v_n]$， 范得蒙矩阵的一般形式为：
$$ V= \begin{bmatrix} v_1^{n-1} & \cdots & v_1^2 & v_1^1 & 1 \\ v_2^{n-1} & \cdots & v_2^2 & v_2^1 & 1 \\ v_3^{n-1} & \cdots & v_3^2 & v_3^1 & 1 \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ v_n^{n-1} & \cdots & v_n^2 & v_n^1 & 1 \\ \end{bmatrix} $$
范德蒙（Vandermonde）矩阵是法国数学家范德蒙提出的一种特殊矩阵。范得蒙矩阵的最后一列全为1，即向量v各元素的零次方，倒数第二列为指定的向量v，即向量v各元素的一次方， 其他各列是其后列与倒数第二列的点乘积。
在 Matlab 中，函数vander(V)生成以向量V为基础的范得蒙矩阵。
例2.1.4：
>> A = vander(1:5)
A =
1 1 1 1 1
16 8 4 2 1
81 27 9 3 1
256 64 16 4 1
625 125 25 5 1范德蒙矩阵常用在各种通信系统的纠错编码中，例如，常用的Reed-Solomon编码即以范德蒙矩阵为基础。
希尔伯特矩阵
n 阶希尔伯特（Hilbert）矩阵的一般形式为：
$$ H= \begin{bmatrix} 1 & \cfrac{1}{2} & \cfrac{1}{3} & \cdots & \cfrac{1}{n} \\ \cfrac{1}{2} & \cfrac{1}{3} & \cfrac{1}{4} & \cdots & \cfrac{1}{n+1} \\ \cfrac{1}{3} & \cfrac{1}{4} & \cfrac{1}{5} & \cdots & \cfrac{1}{n+2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \cfrac{1}{n} & \cfrac{1}{n+1} & \cfrac{1}{n+2} & \cdots & \cfrac{1}{2n-1} \\ \end{bmatrix} $$
希尔伯特矩阵的元素为$H(i,j) = \cfrac{1}{i+j-1}$。
在 Matlab 中，生成n阶希尔伯特矩阵的函数是hilb(n)。
例2.1.5：
>> format rat #输出格式为有理输出
>> H=hilb(4)
H =
1 1/2 1/3 1/4
1/2 1/3 1/4 1/5
1/3 1/4 1/5 1/6
1/4 1/5 1/6 1/7希尔伯特矩阵是著名的病态矩阵，即任何一个元素发生较小的变动，整个矩阵的值和逆矩阵都会发生很大变化。病态程度和矩阵的阶数相关，随着阶数的增加病态越严重。
伴随矩阵
设多项式 $p(x) = a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0$，则多项式的伴随矩阵是：
$$ A= \begin{bmatrix} -\cfrac{a_{n-1}}{a_n} & -\cfrac{a_{n-2}}{a_n} & -\cfrac{a_{n-3}}{a_n} & \cdots & -\cfrac{a_1}{a_n} & -\cfrac{a_0}{a_n} \\ 1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 1 & 0 & \cdots & 0 & 0 \\ 0 & 0 & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & 0 & \cdots & 1 & 0 \\ \end{bmatrix} $$
$p(x)$ 称为 $A$ 的特征多项式，方程 $p(x)=0$ 的根称为 $A$ 的特征值。
Matlab生成伴随矩阵的函数是compan(p)，其中p是一个多项式的系数向量，高次幂系数排在前，低次幂排在后。
例2.1.6：
生成多项式 $x^3-2x^2-5x+6$ 的伴随矩阵。
>> p = [1,-2,-5,6]
p =
1 -2 -5 6
>> A = compan(p)
A =
2 5 -6
1 0 0
0 1 0可以求出伴随矩阵的特征值，该特征值等于多项式方程的根。
帕斯卡矩阵
$$ A= \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 1 & 3 & 6 & 10 & 15 & 21 & 28 & 36 \\ 1 & 4 & 10 & 20 & 35 & 56 & 84 & 120 \\ 1 & 5 & 15 & 35 & 70 & 126 & 210 & 330 \\ 1 & 6 & 21 & 56 & 126 & 252 & 462 & 792 \\ 1 & 7 & 28 & 84 & 210 & 462 & 924 & 1716 \\ 1 & 8 & 36 & 120 & 330 & 792 & 1716 & 3432 \\ \end{bmatrix} $$
根据二项式定理，(x+y)n 展开后的系数随着n的增大组成一个三角形表，这个三角形称为杨辉三角形。
把二项式系数依次填写在矩阵的左侧对角线上，然后提取左侧的n行n列元素即为n阶帕斯卡（Pascal）矩阵。
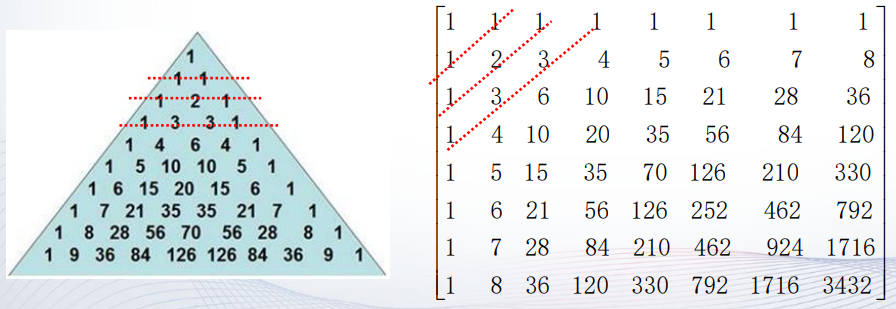
帕斯卡矩阵的第一行元素和第一列元素都为1，其余位置的元素是该元素的左边元素与上面元素相加，即 $P(i,j)=P(i,j-1)+P(i-1,j)$，且 $P(i,1)=1,P(1,j)=1$。
函数pascal(n)生成一个 n 阶帕斯卡矩阵。
例2.1.7：
生成5阶帕斯卡矩阵，验证它的逆矩阵的所有元素也为整数。
>> format rat
>> P = pascal(5)
P =
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
>> inv(P)
ans =
5 -10 10 -5 1
-10 30 -35 19 -4
10 -35 46 -27 6
-5 19 -27 17 -4
1 -4 6 -4 1 
