【Matlab学习1.5】矩阵元素的引用
矩阵元素的引用方式
矩阵元素的引用
下标必须为正数，且用圆括号括起来
A(3,2)表示A矩阵第3行第2列的元素，如：>> A(3,2) = 200
例1.5.1：
>> A = [1,2,3;4,5,6];
>> A(4,5) = 10
A =
1 2 3 0 0
4 5 6 0 0
0 0 0 0 0
0 0 0 0 10由此可见：如果给出的行下标或列下标大于原来矩阵的行数和列数，那么Matlab将自动扩展原来的矩阵，并将扩展后没有赋值的矩阵元素置为0。
通过序号来引用
在 Matlab 中，矩阵元素按列存储，即首先存储矩阵的第一列元素，然后存储第二列元素，…，一直到矩阵的最后一列元素。
矩阵元素的序号就是矩阵元素在内存中的排列顺序。
例1.5.2：
>> A = [1,2,3;4,5,6]
A =
1 2 3
4 5 6
>> A(3)
ans =
2由此可见：序号与下标是一一对应的，以 m×n 矩阵 A 为例，矩阵元素A(i,j)的序号为 (j-1)×m+i。
下标与序号互换函数
矩阵元素的序号与下标可以利用 sub2ind 和 ind2sub 函数实现相互转换。
sub2ind 函数
将矩阵中指定元素的行、列下标转换成存储的序号。
调用格式为：D = sub2ind(S,I,J)，即#序号 = sub2ind(行数和列数组成的向量,转换矩阵的行下标,转换矩阵的列标)。
其中 S 一般由 size 函数获取。
如果 I 和 J 是矩阵，表示要将矩阵中的多个元素的行列下标转换为存储的序号，那么 I 和 J 的行列数必须相同。
D 为对应下标元素的序号，它的行列数与 I 和 J 相同。
例1.5.3：
>> A = [1,3;4,6]
A =
1 3
4 6
>> A = [1:3;4:6]
A =
1 2 3
4 5 6
>> D = sub2ind(size(A),[1,2;2,2],[1,1;3,2])
D =
1 2
6 4说明在一个2×3的矩阵中，下标为(1,1), (2,1), (2,3), (2,2)的元素序号分别为1,2,6,4。
ind2sub 函数
将把矩阵元素的序号转换成对应的下标。
调用格式为：[I,J] = ind2sub(S,D)，即[行下标,列下标] = ind2sub(行数和列数组成的向量,序号)。
例1.5.4：
>> [I,J] = ind2sub([3,3],[1,3,5])
I =
1 3 2
J =
1 1 2说明在一个3×3的矩阵中，序号为1,3,5的元素的下标分别为(1,1), (3,1), (2,2)。
利用冒号表达式获得子矩阵
子矩阵是指由矩阵中的一部分元素构成的矩阵。
既可以用冒号表达式作为引用矩阵的下标，也可以用单个的冒号作为行下标或列下标，代表全部行或全部列。
>> A(i,:) #第i行的全部元素
>> A(:,j) #第j列的全部元素
>> A(i:i+m,k:k+m) #第i～i+m行内且在第k～k+m列中的所有元素
>> A(i:i+m,:) #第i～i+m行的全部元素例1.5.5：
>> A = [1:5;6:10;11:15]
A =
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
>> A(1:2,:) #A矩阵的第一行和第二行
ans =
1 2 3 4 5
6 7 8 9 10
>> A(2:3,1:2:5) #A矩阵的第二行和第三行，第一列、第三列和第五列（第一列到第五列，步长为2）
ans =
6 8 10
11 13 15end 运算符：
表示某一维的末尾元素下标。
例1.5.6：
>> A = [1:5;6:10;11:15;16:20];
>> A(end,:) #最后一行
ans =
16 17 18 19 20
>> A([1,4],3:end) #第一行和第四行，第三列到最后一列
ans =
3 4 5
18 19 20思考：
设x是一个向量，x的倒数第2个元素如何表示？
答案：
x(end-1)
利用空矩阵删除矩阵的元素
空矩阵是指没有任何元素的矩阵。
>> x = [] #X是一个空矩阵。
x =
[]例1.5.7：
>> A = [1,2,3,0,0;7,0,9,2,6;1,4,-1,1,8]
A =
1 2 3 0 0
7 0 9 2 6
1 4 -1 1 8
>> A(:,[2,4]) = [] #将A矩阵的第二列和第四列设为空矩阵
A =
1 3 0
7 9 6
1 -1 8例1.5.8：
（1）命令X=[]与clear X有何不同？请上机验证结论。
（2）有以下语句，说出x1、x2、x3的区别，并上机验证结论。
x = [1:4;4,3,5,8]x1 = x(2:1)x2 = []x3 = 2:1
#提示：依次执行下列语句，用isempty函数判断矩阵是否为空矩阵，用size函数确定矩阵每一维的大小，根据语句执行结果总结规律。
>> x = [1:4;4,3,5,8]
>> x1 = x(2:1)
>> x2 = []
>> x3 = 2:1
>> [isempty(x),isempty(x1),isempty(x2),isempty(x3)]
>> [size(x);size(x1);size(x2);size(x3)]答案：
（1）X=[]是将X设置为空矩阵，clear X是将X删除
（2）
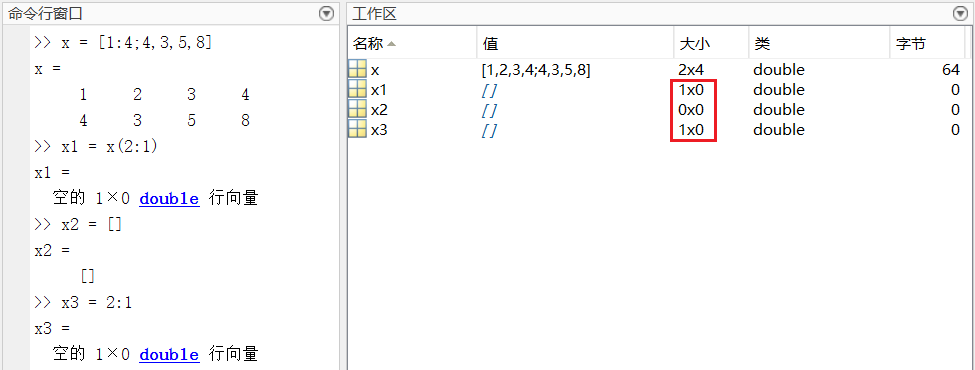
x1 = x(2:1)创建空的 1×0 double 行向量；x2 = []创建空的 0×0 空矩阵；x3 = 2:1设置空的 1×0 double 行向量。
改变矩阵的形状
reshape 函数
reshape(A,m,n)：在矩阵总元素保持不变的前提下，将矩阵A重新排成m×n的二维矩阵
注意：reshape函数只是改变原矩阵的行数和列数，但并不改变原矩阵元素个数及其存储顺序。
例1.5.9：
>> x = [23,45,65,34,65,34,98,45,78,65,43,76];
>> y = reshape(x,3,4)
y =
23 34 98 65
45 65 45 43
65 34 78 76A(:)
将矩阵A的每一列元素堆叠起来，成为一个列向量。
>> A =[-45,65,71;27,35,91]
A =
-45 65 71
27 35 91
>> B=A(:)
B =
-45
27
65
35
71
91
#本例题中A(:)等价于reshape(A,6,1)
