【Matlab学习1.2】数值数据

数值数据类型的分类

整型

Y = int8(X) 将 X 中的值转换为 int8 类型。超出范围 [-2⁷, 2⁷-1] _{（二进制）}的值映射到最近的端点。（对比C语言，当一个整数的值超出了它的存储范围时，就会发生溢出。）

对比：

当一个整数的值超出了它的存储范围时结果

C语言

发生溢出

例1.2.1：

#include<stdio.h>
int main()
{
	short int x[4], i;    #short int的存储数值为-32768~32767
	x[0] = 32768;
	x[1] = 40000;
	x[2] = -32768;
	x[3] = -40000;
	for(i=0;i<4;i++)
		printf("%d\n", x[i]);
	return 0;
}

最终输出的结果为
-32768
-25536
32767
25536

说明发生溢出
（具体原理请了解补码相关知识，证明从略）

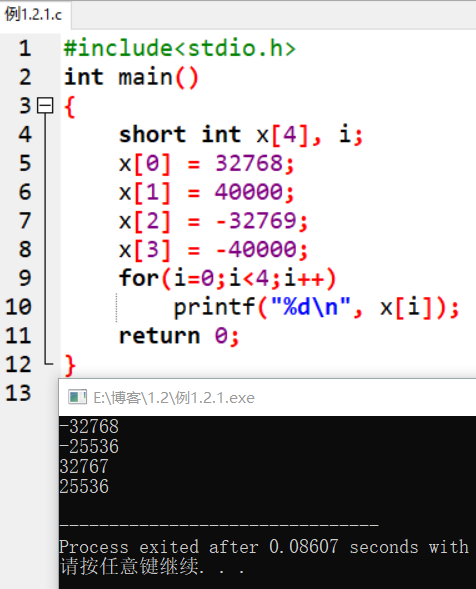Matlab

映射到最近的端点。

例1.2.2：

#int16的存储数值为-32768~32767
>> int16(32768)
>> int16(40000)
>> int16(-32769)
>> int16(-40000)

最终输出的结果为
32767
32767
-32768
-32768

说明映射到最近的端点。

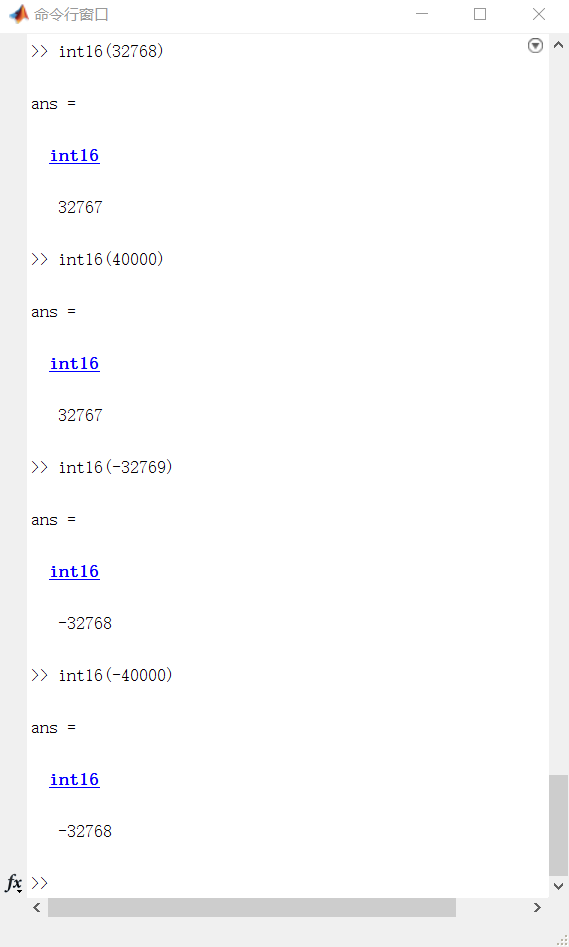易错点注意：

输入时是int8()或uint16()等等，不是int()，int 函数是计算定积分和不定积分的函数。

例1.2.3：

#int8的存储数值为-128~127
#uint8的存储数值为0~255
>> x = int8(129)
>> x = uint8(129)
>> x = int8(-128)
>> x = uint8(-128)

最终输出结果为
127
129
-128
0

例1.2.3

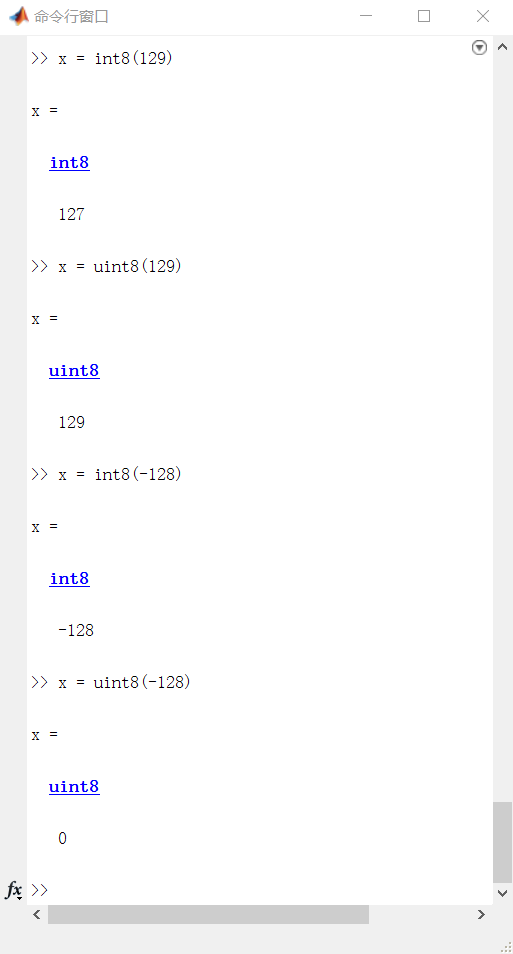
注：在其存储范围内的小数转化为整数时，会采用四舍五入的办法取整（类似之后提到的 round 函数）。

浮点型

浮点型数据分为单精度型和双精度类型，单精度型实数在内存中占用4个字节，而双精度型实数在内存中占用8个字节.所以双精度型的数据精度更高。

single 函数：将其他类型的数据转换为单精度型。（区别于C语言中的 float ）
double 函数：将其他类型的数据转换为双精度型。

例1.2.4：

#class函数用于返回类的名称。
>> class(4)
>> class(single(4))

例1.2.4

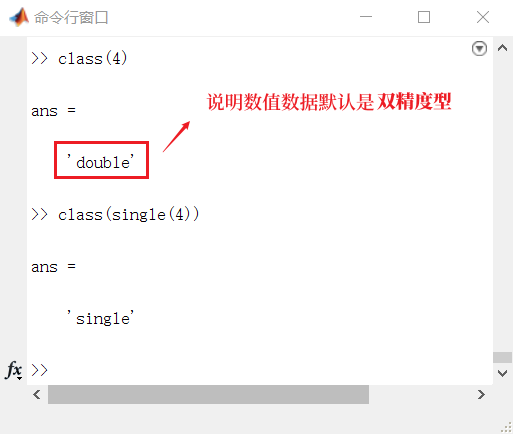
由此说明，在 Matlab 中，数值数据默认是双精度型（double）。

涉及整数和浮点数的算术运算时，个人感觉是先全部转化成精度最高的数据类型进行计算，再将结果转化为精度最低的数据类型输出。

复型

复型数据包括实部和虚部两个部分，实部和虚部默认为双精度型，虚数单位用i或j来表示。

real 函数：求复数的实部。
imag 函数：求复数的虚部。

例1.2.5：

在 Matlab 中输入下列代码，并思考在 Matlab 中，3 + 4i 和 3 + 4 * i 有区别吗？

>> clear
>> 3 + 4i
>> 3 + 4j

>> i = 5;
>> 3 + 4i
>> 3 + 4 * i
>> 3 + 4 * j
>> 3 + 4j

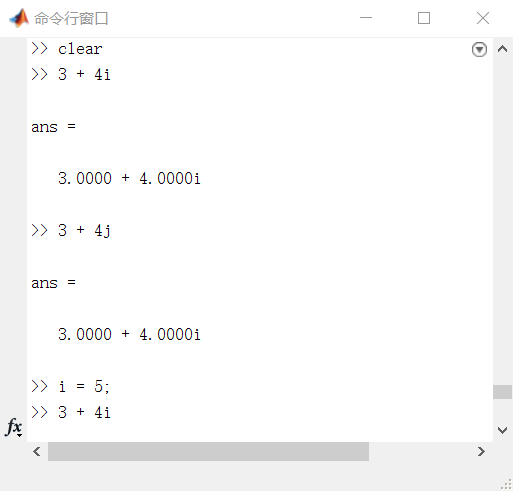
例1.2.5-1

例1.2.5-2

当 i 未被赋值时，3 + 4i，3 + 4 * i，3 + 4 * j 和 3 + 4j 的执行结果均为 3.0000 + 4.0000i
当 i 被赋值时，3 + 4 * i 就是一个算术表达式

数值数据的输出格式

可以用 format 函数来设置数值数据的输出格式

例1.2.6：

>> format long
>> 50/3
>> format 
>> 50/3

例1.2.6

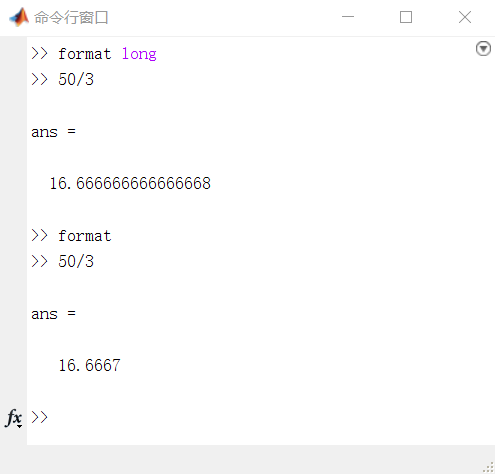
有关 format 函数

点击跳转官方文档——设置输出显示格式

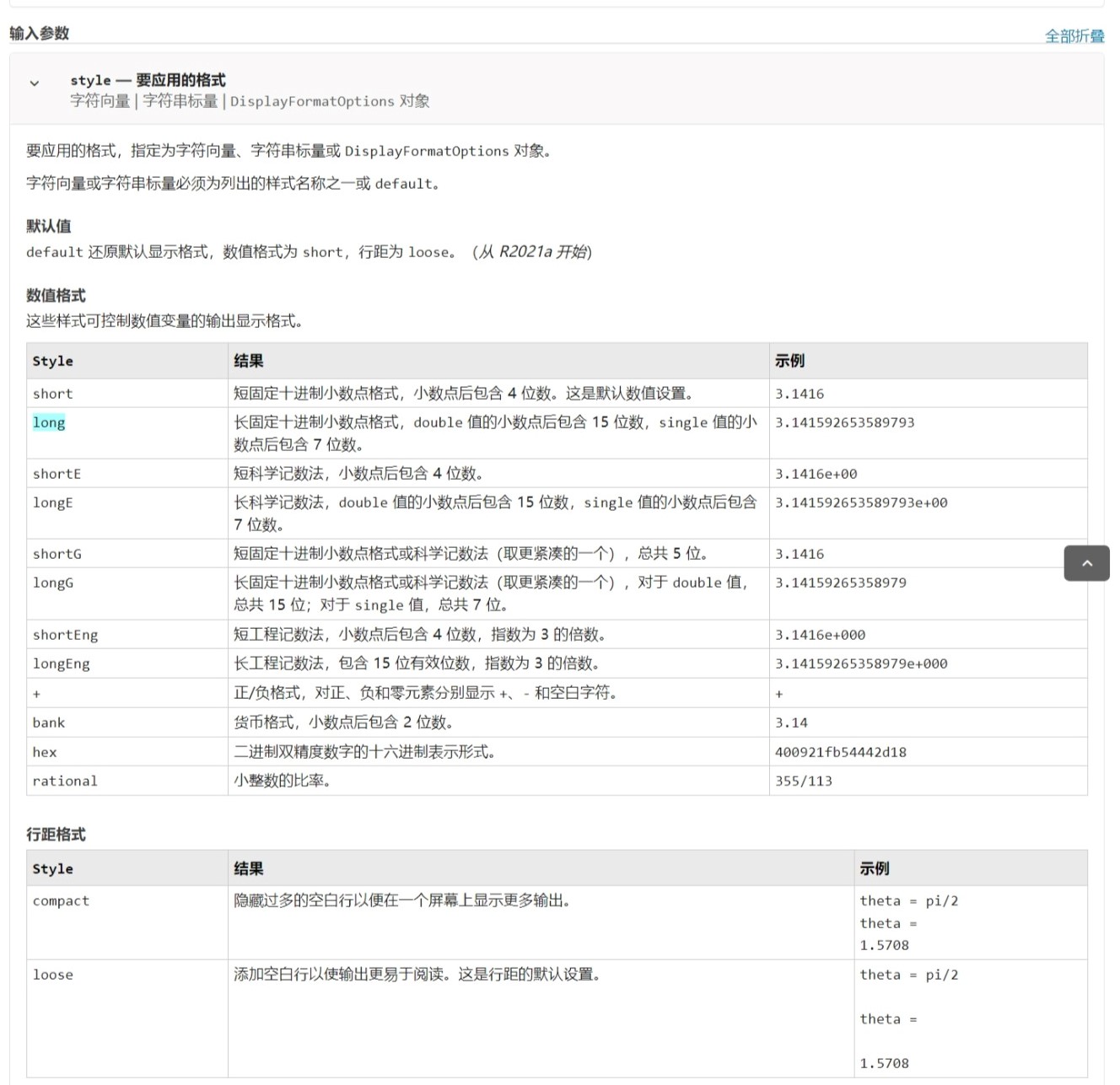
format函数输入函数

常用数学函数

函数的调用格式

函数的调用格式为：函数名（函数自变量的值）

例1.2.7：

>> A=[4,2;3,6]
>> B=exp(A)

例1.2.7

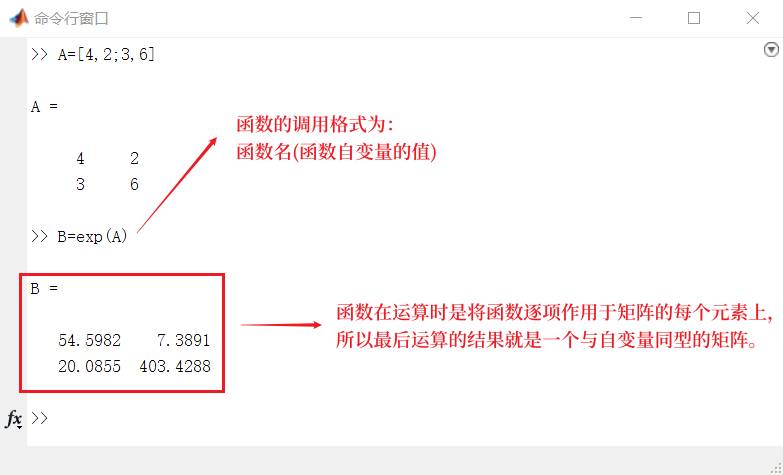
函数在运算时是将函数逐项作用于矩阵的每个元素上，所以最后运算的结果就是一个与自变量同型的矩阵。

常用函数的应用

各个函数应用举例详见最后例1.2.8

更多有关初等函数的介绍详见官方文档——初等数学 — 函数

e^x

^exp(x)表示 e^x。

（指数： exponent）

三角函数

三角函数有以弧度为单位的函数和以角度为单位的函数，如果是以角度为单位的函数就在函数名后面加“d”，以示区别。

>> sin(pi/2)    #sin函数计算弧度
>> sind(90)     #sind函数计算角度

更多有关三角函数的函数详见官方文档——三角学（结果以弧度或度为单位的正弦、余弦和相关函数）

abs 函数

abs 函数可以求实数的绝对值、复数的模、字符串的 ASCII 码值。

取整的函数

用于取整的函数有fix、floor、ceil、round。

	英语含义	Matlab 中取整规则
round	(BrE) round = around 大约	四舍五入
ceil	ceiling n. 天花板；最高限度	向上取整取大于等于这个数的第一个整数。
floor	floor n. 地板；底价	向下取整取小于等于这个数的第一个整数
fix	fix n. 固定	固定取靠近0的那个整数也就是舍去小数取整

余数

rem函数	mod函数
求余运算	取模运算
`r = rem(a,b)` 返回 `a` 除以 `b` 后的余数，其中 `a` 是被除数，`b` 是除数	`b = mod(a,m)` 返回 `a` 除以 `m` 后的余数，其中 `a` 是被除数，`m` 是除数
表达式为 `r = a - b.*fix(a./b)`	表达式为 `b = a - m.*floor(a./m)`
rem函数遵从 `rem(a,0)` 是 `NaN` 的约定	mod函数遵从 `mod(a,0)` 返回 `a` 的约定
rem函数生成一个为零或与被除数具有相同符号的结果	mod函数生成一个为零或与除数具有相同符号的结果

质数/素数

TF = isprime(X) 返回与 X 大小相同的逻辑数组。如果 X(i) 为质数，则 TF(i) 的值为 true；否则，值为 false。

find 函数

find 函数查找非零元素的索引。

对数函数

Y = log(X) 返回数组 X 中每个元素的自然对数 ln(x)。

Y = log2(X) 计算 X 的元素以 2 为底的对数。

Y = log10(X) 返回数组 X 中每个元素的常用对数（以 10 为底）。

例1.2.8 函数应用举例：

函数应用举例1——上述各函数举例：

#exp函数举例
>> exp(3)
ans =
   20.0855


#三角函数举例
>> sin(pi/2)
ans =
    1
>> sind(90)
ans =
    1


#abs函数举例
>> abs(-4)
ans =
    4
>> abs(3+4i)
ans =
    5
>> abs('a')
ans =
    97


#取整函数举例
>> round(4.7)
ans =
    5
>> fix(-3.2)
ans =
    -3
>> floor(3.6)
ans =
    3
>> ceil(-3.8)
ans =
    -3


#余数函数举例
>> rem(100,3)
ans =
     1
>> mod(100,3)
ans =
     1

>> rem(-100,3)
ans =
    -1
>> mod(-100,3)
ans =
     2

>> rem(100,-3)
ans =
     1
>> mod(100,-3)
ans =
    -2


#isprime函数举例
>> isprime(12)
ans =
  logical
   0
>> isprime(17)
ans =
  logical
   1


#find函数举例
#在 3×3 矩阵中查找非零元素
>> X = [1 0 2; 0 1 1; 0 0 4]
X =
     1     0     2
     0     1     1
     0     0     4
>> k = find(X)    #查看非零元素对应索引
k =
     1
     5
     7
     8
     9
>> X(k)    #查看 X 的对应元素
ans =
     1
     1
     2
     1
     4
    
    
#对数函数举例
>> log(10)
ans =
    2.3026
>> log2(256)
ans =
     8
>> log10(0.01)
ans =
    -2

函数应用举例2——分别求一个三位正整数的个位数字、十位数字和百位数字：

>> m = 345;
>> m1 = rem(m,10)
m1 =
    5
>> m2 = rem(fix(m/10),10)
m2 =
    4
>> m3 = fix(m/100)
m3 =
    3

函数应用举例3——求[1,100]区间的所有素数：

>> x = 1:100;
>> k = isprime(x);
>> k1 = find(k);
>> p = x(k1)
p =
  列 1 至 13
     2     3     5     7    11    13    17    19    23    29    31    37    41
  列 14 至 25
    43    47    53    59    61    67    71    73    79    83    89    97

思考：求以5为底的对数，该如何计算？

答案：

利用换底公式 $\log _{a}(b)=\cfrac{\log _{c}(b)}{\log _{c}(a)}$，通过log()、log2()和log10()构造出换底后的式子。

例1.2.9：

求 $\log _{5}(29)$ 的值。

由换底公式可知 $\log _{5}(29)=\cfrac{\ln29}{\ln5}$。

>> log(29)/log(5)
ans =
    2.0922

posted @ 2023-01-28 10:59 SplendidCrepuscule 阅读(244) 评论(0) 编辑收藏举报

刷新页面返回顶部

Splendid Crepuscule