摘要：本文描述了两种状态重构算法，使用了被稀疏且任意的“噪声”破坏的测量数据来估计状态。我们的出发动机是保护信息物理系统，以免受到来自恶意对手的传感器攻击。第一个算法从一批传感器测量中重构状态，而第二个算法被构造为龙伯格观测器的形式，能够及时使用最新的测量数据。这些算法的一个显著亮点是使用事件触发技术来提高计算性能。
关键词：事件触发观测器、安全信息物理系统、安全状态重构、传感器攻击。
系统模型：
考虑以下线性离散时间控制系统：
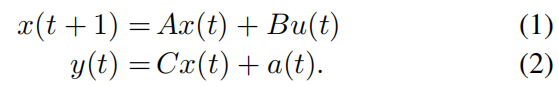
将一段采样后的输出方程写成增广形式：
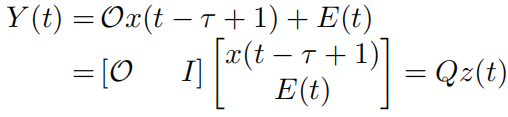
构造下面的最优化问题：
显然，上式的最小值为0，且当Y=Qz时才会取到。另外，我们注意到Q矩阵的形状是水平长条（变量数少于约束数），根据线性代数的知识，我们可以判断Y=Qz的解有多个。所以若不加以约束，上式无法求解。下面的定理3.2解决了这一问题：
定理3.2说明，“问题2.3有唯一解”和“系统2s稀疏能观”这两个命题之间是等价的。下面是证明思路：
1、首先，最优问题有唯一解 等价于 “f(x,E)=Ox+E”是单射 。
2、证明原 if 命题的逆否命题：若Ox+E不是单射（即最优问题有多解），则系统也不是2s稀疏能观。此时可以得到O(x1-x2)=E2-E1，显然E2-E1含有最多2s个非零元素。将这2s行去掉后，O_gamma(x1-x2)=0，即Y_gamma=O_gamma*x1=O_gamma*x2。这个式子意味着子系统（A，C_gamma）不是能观的（能观性的定义），即原系统不是2s稀疏能观的，证明完毕。
3、证明原 only if 命题的逆否命题：若系统不是2s稀疏能观，则Ox+E不是单射（即最优问题有多解）。由已知可得，存在某个子系统（A，C_gamma）不是能观的，故该子系统的输出方程满足：Y_gamma=O_gamma*x1=O_gamma*x2，将去掉的<=2s行分成两个基数小于s的集合gamma1和gamma2，然后以此构造合适的攻击向量E1和E2，可以得到O(x1-x2)=E2-E1，这个式子意味着Ox+E不是单射。
事实上，我们还可以找到更多的等价命题，比如在另一篇论文中有：
其中（i）和（ii）和上面的定理3.2中一样，这里只需要证明（ii）和（iii）等价：
注：引理4.1中的Q和之前的Q不一样，它在这里为I - O*inv(O'O)*O'。
矩阵A列满秩等价于A'A可逆；
判断一个矩阵是不是对称矩阵，计算A'；
对于n阶实对称矩阵A，下面两个条件等价：1、存在秩为n的m×n实矩阵B，使A=B′B；2、A是正定矩阵；
两次使用舒尔补引理
Q矩阵的特殊性
一些与初等矩阵相关的运算技巧
这些命题共同描述了在无扰动情况下，状态和攻击估计值zˆ的唯一性。
2s受限特征值：
