摘要:信息物理系统(Cyber-physical systems (CPSs))在稀疏传感器攻击下的安全状态估计问题(Secure state estimation,SSE)是指:从被污染的测量值中估计出系统状态。虽然这一问题可以通过蛮力搜索(brute force search)来解决,但随着传感器排列组合的数量增加,算法的时间需求也会急剧上升,这阻碍了该方法的可扩展性(scalability)。为了降低计算复杂度,本文提出了一种替代方法(称为集合覆盖,set cover),利用贪婪算法将候选传感器的数量减少至少一半。然后,设计一个切换观测算法,使用较少的候选观测器,在基本可观测性要求下从损坏的测量中估计状态。此外,基于观测器的设计条件,我们提出了一种改进的贪婪算法来进一步减少候选传感器的数量。最后,通过两个模拟证明了所提出的集覆盖方法的有效性,表明执行时间减少了一个数量级。
关键词——信息物理系统(CPSs)、线性矩阵不等式(LMI)、集合覆盖方法、稀疏传感器攻击、切换龙伯格观测器。
系统描述
考虑一类以线性离散时间形式描述的系统:
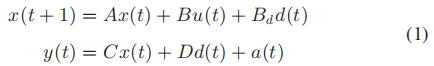
设测量通道的数量为ny;a(t)∈Rny是攻击信号,d(t)∈Rnd是有界扰动。
通过收集τ个连续的观测值(从t−τ+1到t,t≥τ),系统(1)可以重写如下:
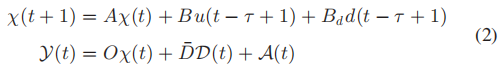
预先做出如下假设和定义:
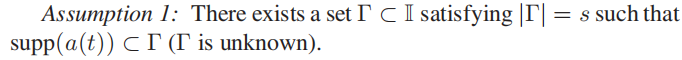
假设1意味着攻击信号是s稀疏的,即攻击向量中的非零元素不超过s个。注意到,Γ以外的元素一定不会受到攻击,Γ包含的元素则有可能受到了攻击。
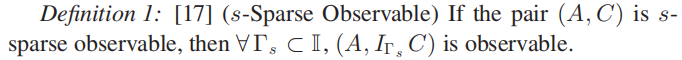
定义1描述了s稀疏能观性,即从C中去掉任意s行,得到的子系统仍然是能观的。显然,要想判断系统的s稀疏能观性,就需要判断一系列子系统的能观性。

假设2说明本文考虑的系统是2s稀疏能观的,在之前很重要的一篇论文中证明了这一命题是进行安全状态估计的充要条件。并且还有一系列论文研究了“系统2s稀疏能观”的其它等价说法。
问题转化
我们希望所设计的状态估计算法得到的结果无限接近于真实的状态,即下面这个式子当无噪声时等于0,当有噪声时存在上界:
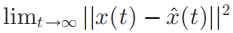
但我们在估计时可以直接使用的只有测量数据Y,所以第一步要证明一定条件下,残差趋于0和状态趋于0之间的等价关系。引理1和引理2都描述了这一点:

这里的s^是我们假定的受攻击的传感器的个数,正常情况下它应该就等于s,但本文讨论的集合覆盖方法需要将它假设为2s。
引理1使用被选中的那些测量来构造李雅普诺夫函数,引理2则使用全部的测量来构造李雅普诺夫函数,但是需要预先估计出攻击信号。
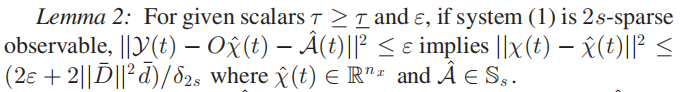



 浙公网安备 33010602011771号
浙公网安备 33010602011771号