【语言处理与Python】10.1自然语言理解\10.2命题逻辑
10.1自然语言理解
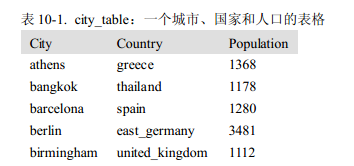
查询数据库
如果有人提出一个问题:
Which country is Athens in?
得到的回答应该是:
Greece.
这个数据可以通过数据库语言得到答案:
SELECT Country FROM city_table WHERE City= 'athens'
这里有一个文法,可以把句子转换成SQL语句:
>>>nltk.data.show_cfg('grammars/book_grammars/sql0.fcfg') %start S S[SEM=(?np+ WHERE+ ?vp)] -> NP[SEM=?np]VP[SEM=?vp] VP[SEM=(?v+ ?pp)] -> IV[SEM=?v] PP[SEM=?pp] VP[SEM=(?v+ ?ap)] -> IV[SEM=?v] AP[SEM=?ap] NP[SEM=(?det+ ?n)] -> Det[SEM=?det]N[SEM=?n] PP[SEM=(?p+ ?np)] -> P[SEM=?p]NP[SEM=?np] AP[SEM=?pp]-> A[SEM=?a]PP[SEM=?pp] NP[SEM='Country="greece"']-> 'Greece' NP[SEM='Country="china"']-> 'China' Det[SEM='SELECT']-> 'Which' | 'What' N[SEM='CityFROMcity_table'] -> 'cities' IV[SEM=''] -> 'are' A[SEM='']-> 'located' P[SEM='']-> 'in' 这使我们能够分析SQL查询: >>>from nltk import load_parser >>>cp = load_parser('grammars/book_grammars/sql0.fcfg') >>>query ='What cities are located in China' >>>trees = cp.nbest_parse(query.split()) >>>answer = trees[0].node['sem'] >>>q= ' '.join(answer) >>>print q SELECT City FROM city_table WHERE Country="china"
要达到能够从句子到后来的生成的数据库SQL语句,也就是独立于任何的查询语言,我们应该建立一个经典的逻辑的标准解释。
逻辑形式更加的抽象,更加的通用。
自然语言、语义和逻辑
一个句子集W的模型是某种情况的形式化表示,其中w中的所有句子都为真。
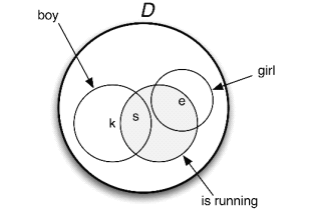
看下面这个图:
段落的域D(我们当前关心的所有实体)是个体的一个集合,而当集合从D建立,关系也被确立。
例如:
域D包括3个孩子,Stefan、Klaus和Evi,分别用s、k和e表示。记为D= {s,k,e}。
表达式boy是包含Stefan和Klaus的集合,表达式girl是包含Evi的集合,表达式is running是包含Stefan和Evi的集合。
10.2命题逻辑
我们要设计一种逻辑语言,使推理更加的明确。
[Klaus chased Evi]and [Evi ran away]
φ和ψ替代(8)中的两个子句,并用&替代对应的英语词and的逻辑操作:φ&ψ。这就是这句话的逻辑形式。
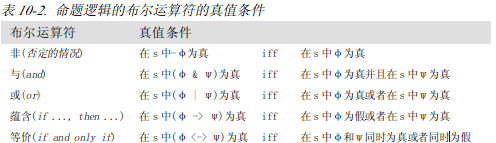
下面的标重,指定了包含一些运算符的公式为真的条件。iff作为if and only if(当且仅当)的缩写。
注意蕴含这个运算符:
形式(P ->Q)的公式是为假只有当P为真并且Q为假时。如果P为假(比如说,P对应Themoonis madeofgreen cheese)而Q为真(比如说,Q对应Twoplus two equa ls four)那么P -> Q的结果为真。
NLTK中的inference模块通过一个第三方定理证明器Prover9的接口,可以进行逻辑证明。
例如:
SnF表示:Sylvania is to the north of Freedonia。
Fns表示:Freedonia is to the north of Sylvania。
>>>lp =nltk.LogicParser() >>>SnF= lp.parse('SnF') >>>NotFnS= lp.parse('-FnS') >>>R= lp.parse('SnF -> -FnS') >>>prover= nltk.Prover9() >>>prover.prove(NotFnS,[SnF, R]) True
一个命题逻辑的模型,需要为每个可能的公式分配值True或False.
我们可以来简单做一个实验:
1、先为每个命题符号分配一个值
>>>val = nltk.Valuation([('P',True),('Q', True),('R', False)])
我们可以查看这个值的:
>>>val['P'] True
2、为了简化实验,我们先忽略dom和g的设置
>>>dom =set([])
>>>g= nltk.Assignment(dom)
3、使用val来初始化模型m
>>>m=nltk.Model(dom, val)
4、每个模型都有一个evaluate()方法,可以确定逻辑表达式。例如:
>>>print m.evaluate('(P&Q)',g) True >>>print m.evaluate('-(P&Q)',g) False >>>print m.evaluate('(P&R)',g) False >>>print m.evaluate('(P| R)',g) True
现在,我们只是局限在用字母P、Q等表示原子,句子。但是我们需要超越命题逻辑到一个更有表现力的东西,能够看到里面的基本的句子,也就是一阶逻辑。