【语言处理与Python】8.2文法有什么用?\8.3上下文无关文法\8.4上下文无关文法分析
8.2文法有什么用?
超越n-grams
用bigrams中的频率信息生成句子,短的时候可以接收,但是长的时候就显得无法接受。
我们系统地可以用较短的序列替代较长的序列,并使其依然符合语法规则。
例如下面这句话:
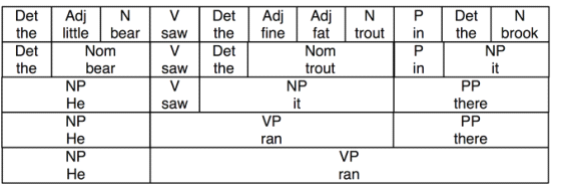
我们可以为这幅图上添上文法类别标签。
NP为名词短语;VP为动词短语;PP为介词短语;
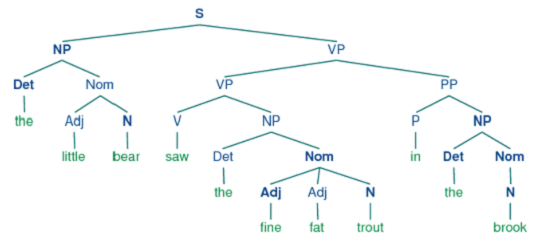
用树来表示:
句子可以有任意的长度。短语结构树可以有任意深度。
在下一节中,将看到一个指定的文法如何将句子细分成它的直接成分,以及如何将这些进一步细分,直到到达单独词汇层面。
8.3上下文无关文法
context-free grammar,CFG上下文无关文法(更多关于上下文无关文法请自行了解)
grammar1= nltk.parse_cfg(""" S -> NPVP VP-> VNP| VNPPP PP-> P NP V-> "saw" | "ate" | "walked" NP-> "John" | "Mary" | "Bob" | DetN| DetNPP Det-> "a" | "an" | "the" | "my" N-> "man" | "dog" | "cat" | "telescope" | "park" P-> "in" | "on" | "by" | "with" """) >>>sent = "Mary saw Bob".split() >>>rd_parser =nltk.RecursiveDescentParser(grammar1) >>>for tree in rd_parser.nbest_parse(sent): ... print tree (S (NP Mary)(VP (V saw) (NP Bob)))
写自己的文法
我们可以写自己的文法,保存在cfg的文件中。
>>>grammar1= nltk.data.load('file:mygrammar.cfg') >>>sent = "Mary saw Bob".split() >>>rd_parser =nltk.RecursiveDescentParser(grammar1) >>>for tree in rd_parser.nbest_parse(sent): print tree
如果没有任何输出,可能是sent也就是句子不符合文法,可以打开追踪,进行调试和检查。
rd_parser =nltk.RecursiveDescentParser(grammar1, trace=2)
句法结构中的递归
句法递归请参考文法相关资料。
递归深度是没有限制的,我们可以尝试分析更深层次的嵌套结构的句子。
RecursiveDescentParser是无法处理形如X-> XY的左递归。
8.4上下文无关文法分析
在这里介绍两种简单的分析方法,一种自上而下的方法成为递归下降分析,一种自下而上的方法成为移近-归约分析。同样,也会看到更复杂的算法,一种带自下而上过滤的自上而下的方法称为左角落分析。
一种动态规划技术成为图表分析。
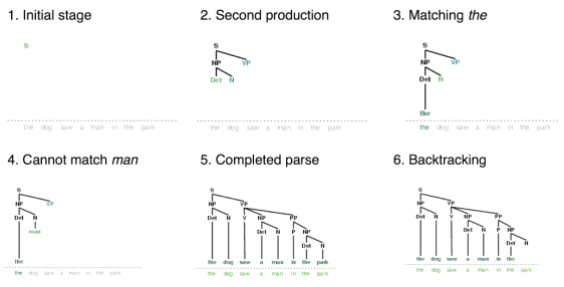
递归下降分析
我们可以使用图形化师范nltk.app.rdparser()中看到递归下降的过程。
从S节点开始匹配。
NLTK提供了一个递归下降分析器:
>>>rd_parser =nltk.RecursiveDescentParser(grammar1) >>>sent = 'Mary saw a dog'.split() >>>for t in rd_parser.nbest_parse(sent): ... print t (S (NP Mary)(VP (V saw) (NP (Det a) (N dog))))
递归下降是有缺点的:
1、左递归产生式会进入死循环。
2、分析器浪费了很多时间处理不符合输入句子的词和结构
3、回溯过程中可能丢弃分析过的成分,他们需要在之后重新建立
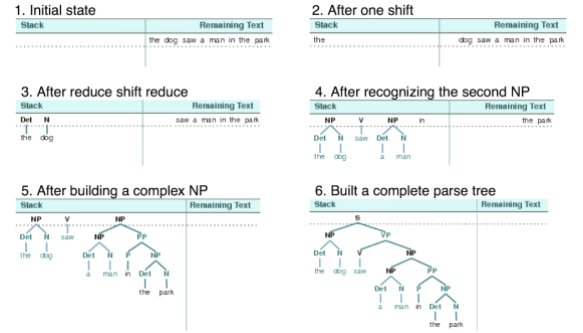
移进-归约分析(简单的自下而上分析)
移位:分析器反复将下一个输入词推到堆栈中,这是移位操作。
归约:如果堆栈上的前N项匹配一些产生式右侧的N个项目,那么就把他们弹出栈,并把产生式左边的项目压入栈。这种替换的操作就是归约操作。
同样,可以使用图形化示范nltk.app.srparser()
相关代码:
>>>sr_parse= nltk.ShiftReduceParser(grammar1) >>>sent = 'Mary saw a dog'.split() >>>print sr_parse.parse(sent) (S (NP Mary)(VP (V saw) (NP (Det a) (N dog))))
左角落分析器
递归下降分析器的问题之一就是不能处理左递归,会进入无限循环。左角落分析器是我们已经看到的自下而上与自上而下的方法的混合体。
他不会陷入左递归产生式的陷阱。在开始工作之前,左角落分析器预处理上下文无关文法建立一个表,其中每行包括两个单元。第一个存放非终结符,第二个存放那个非终结符可能的左角落集合。
例如,grammar2的文法:
grammar2= nltk.parse_cfg(""" S -> NP VP NP-> Det Nom| PropN Nom-> Adj Nom| N VP-> V Adj| VNP| VS| VNPPP PP-> P NP PropN-> 'Buster' | 'Chatterer' | 'Joe' Det-> 'the' | 'a' N-> 'bear' | 'squirrel' | 'tree' | 'fish' | 'log' Adj -> 'angry' | 'frightened' | 'little' | 'tall' V-> 'chased' | 'saw' | 'said' | 'thought' | 'was' | 'put' P-> 'on' """)
他的左角落为:
分析器每次考虑产生式时,他会检查下一个输入词是否与左角落表格中至少一种非终结符的类别相容。
符合语句规则的字串表
上面讨论的简单的分析器在完整性和效率上都有限制,为了弥补这些,我们将运用动态规划算法设计技术解决问题。
这里介绍图表分析。有一个表格需要我们注意,符合语法规则的字串表,简称为WFST。
以这句话为例子:
>>>text = ['I', 'shot', 'an', 'elephant', 'in', 'my', 'pajamas']
如何构建WFST:
def init_wfst(tokens, grammar): numtokens= len(tokens) wfst= [[None for i in range(numtokens+1)] for j in range(numtokens+1)] for i in range(numtokens): productions = grammar.productions(rhs=tokens[i]) wfst[i][i+1]= productions[0].lhs() return wfst def complete_wfst(wfst,tokens, grammar,trace=False): index = dict((p.rhs(),p.lhs()) for pin grammar.productions()) numtokens= len(tokens) for span in range(2, numtokens+1): for start in range(numtokens+1-span): end = start + span for midin range(start+1, end): nt1,nt2 = wfst[start][mid],wfst[mid][end] if nt1 and nt2 and (nt1,nt2) in index: wfst[start][end]= index[(nt1,nt2)] if trace: print "[%s] %3s[%s] %3s[%s] ==>[%s] %3s[%s]" % \ (start, nt1, mid,nt2,end, start, index[(nt1,nt2)], end) return wfst def display(wfst,tokens): print '\nWFST ' + ' '.join([("%-4d" %i) for i in range(1, len(wfst))]) for i in range(len(wfst)-1): print "%d " %i, for j in range(1, len(wfst)): print "%-4s" %(wfst[i][j] or '.'), print >>>tokens = "I shot an elephant in mypajamas".split() >>>wfst0= init_wfst(tokens, groucho_grammar) >>>display(wfst0,tokens) WFST1 2 3 4 5 6 7 0 NP . . . . . . 1 . V . . . . . 2 . . Det . . . . 3 . . . N . . . 4 . . . . P . . 5 . . . . . Det . 6 . . . . . . N >>>wfst1= complete_wfst(wfst0, tokens, groucho_grammar) >>>display(wfst1,tokens) WFST1 2 3 4 5 6 7 0 NP . . S . . S 1 . V . VP . . VP 2 . . Det NP . . . 3 . . . N . . . 4 . . . . P . PP 5 . . . . . Det NP 6 . . . . . . N
在其中,要注意index的内容:
要构建index中的内容,需要有下面的步骤,这里把那段代码提取了出来,单独演示:
#对应的文法 >>> groucho_grammar= nltk.parse_cfg(""" S -> NP VP PP -> P NP NP -> Det N| DetN PP| 'I' VP -> V NP| VP PP Det -> 'an' | 'my' N -> 'elephant' | 'pajamas' V -> 'shot' P ->'in' """) #文法的内容 >>> grammar,productions() [S -> NP VP, PP -> P NP, NP -> Det N, NP -> DetN PP, NP -> 'I', VP -> V NP, VP -> VP PP, Det -> 'an', Det -> 'my', N -> 'elephant', N -> 'pajamas', V -> 'shot', P -> 'in'] #index的内容 pprint.pprint(dict((p.rhs(),p.lhs()) for p in groucho_grammar.productions())) {(Det, N): NP, (DetN, PP): NP, (NP, VP): S, (P, NP): PP, (V, NP): VP, (VP, PP): VP, ('I',): NP, ('an',): Det, ('elephant',): N, ('in',): P, ('my',): Det, ('pajamas',): N, ('shot',): V} >>>
相信,读完这个代码,如果懂得了,必然懂得了构建过程的核心思想。