希音面试:亿级用户 日活 月活,如何统计?(史上最强 HyperLogLog 解读)
文章很长,且持续更新,建议收藏起来,慢慢读!疯狂创客圈总目录 博客园版 为您奉上珍贵的学习资源 :
免费赠送 :《尼恩Java面试宝典》 持续更新+ 史上最全 + 面试必备 2000页+ 面试必备 + 大厂必备 +涨薪必备
免费赠送 :《尼恩技术圣经+高并发系列PDF》 ,帮你 实现技术自由,完成职业升级, 薪酬猛涨!加尼恩免费领
免费赠送 经典图书:《Java高并发核心编程(卷1)加强版》 面试必备 + 大厂必备 +涨薪必备 加尼恩免费领
免费赠送 经典图书:《Java高并发核心编程(卷2)加强版》 面试必备 + 大厂必备 +涨薪必备 加尼恩免费领
免费赠送 经典图书:《Java高并发核心编程(卷3)加强版》 面试必备 + 大厂必备 +涨薪必备 加尼恩免费领
免费赠送 资源宝库: Java 必备 百度网盘资源大合集 价值>10000元 加尼恩领取
希音面试:亿级用户 日活 月活,如何统计?(史上最强 HyperLogLog 解读)
尼恩特别说明: 尼恩的文章,都会在 《技术自由圈》 公号 发布, 并且维护最新版本。 如果发现图片 不可见, 请去 《技术自由圈》 公号 查找
尼恩说在前面
在40岁老架构师 尼恩的读者交流群(50+)中,最近有小伙伴拿到了一线互联网企业如得物、阿里、滴滴、极兔、有赞、希音、百度、网易、美团的面试资格,遇到很多很重要的面试题:
- 如何 统计一个 网站 的日活、月活数? 亿级用户的日活、月活,如何统计?
- Bitmaps可用于统计日活吗?
- 亿级用户的日活、月活,Bitmaps可以统计吗?
- 如何 统计一个页面的每天被多少个不同账户访问量(Unique Visitor,UV))?
- 如何 统计用户每天搜索不同词条的个数?
- 如何 统计注册 IP 数?
最近有小伙伴在面试 希音,又遇到了相关的面试题。小伙伴懵了,因为没有遇到过,所以支支吾吾的说了几句,面试官不满意,面试挂了。
所以,尼恩给大家做一下系统化、体系化的梳理,使得大家内力猛增,可以充分展示一下大家雄厚的 “技术肌肉”,让面试官爱到 “不能自已、口水直流”,然后实现”offer直提”。
当然,这道面试题,以及参考答案,也会收入咱们的 《尼恩Java面试宝典PDF》V171版本,供后面的小伙伴参考,提升大家的 3高 架构、设计、开发水平。
最新《尼恩 架构笔记》《尼恩高并发三部曲》《尼恩Java面试宝典》的PDF,请关注本公众号【技术自由圈】获取,回复:领电子书
首先回顾一下:redis 四大统计(基数统计,二值统计,排序统计、聚合统计)的原理 和应用场景
尼恩这边的文章都有一个 基本的规则,从最为基础的讲起。
先看看 常见的四大统计。
第1大统计:基数统计
基数(Cardinality)是指一个集合中不同元素的数量, 或者说统计一个集合中不重复元素的个数。
简单来说: 基数(Cardinality)就是去除重复后的数的个数
例如,对于一个包含重复元素的集合{1, 2, 2, 3, 4, 4, 4},其基数为4,即不同元素的个数。
在Redis中,HashSet /bitmap/ HyperLogLog数据结构都能提供 高效的基数统计,而HyperLogLog算法可以在不保存原始数据的情况下快速计算出一个集合的基数。
第2大统计:二值统计
二值统计通常涉及到将数据分为两个类别或状态,比如成功与失败、是与非等,并对这些类别进行计数和分析。
这种统计方法在处理二分类问题时非常常见,比如在质量控制、用户行为分析等领域。
亿级海量数据查重,如何实现 ? 涉及的是四大统计其中的 二值统计
亿级海量数据黑名单 ,如何存储?涉及的也是四大统计其中的 二值统计
京东面试:亿级 数据查重,亿级 数据黑名单 ,如何实现?(此文介绍了布隆过滤器、布谷鸟过滤器)
第3大统计:排序统计
排序统计涉及将数据按照一定的顺序(如升序或降序)进行排列,以便于分析和比较。
排序统计的例子,比如,可以使用ZSET对排序统计
- 可以 使用ZSET对文章的点赞数排序并分页展示
- 对评论根据时间进行排序
排序算法如快速排序、归并排序、堆排序等,都是排序统计中常用的方法。
第4大统计:聚合统计
聚合统计是一种数据处理技术,它将多个数据记录组合成一个集合,并计算该集合的统计信息,如总和、平均值、最大值和最小值等。
聚合操作通常用于数据仓库和数据分析中,以简化数据并提取有用的信息。
聚合统计的核心在于对数据进行分组(grouping),然后对每个组应用聚合函数(如sum, avg, max, min等)来计算统计值。
日活月活,属于 基数统计的类型
在数学上,基数或势,即集合中包含的元素的“个数”(参见势的比较),是日常交流中基数的概念在数学上的精确化(并使之不再受限于有限情形)。
有限集合的基数,其意义与日常用语中的“基数”相同,例如{{a,b,c}的基数是3。
无限集合的基数,其意义在于比较两个集的大小,例如整数集和有理数集的基数相同;整数集的基数比实数集的小。
日活 、月活名词解释
- DAU日活:(Daily Active User)日活跃用户数量
常用于反映网站、互联网应用或网络游戏的运营情况。DAU通常统计一日(统计日)之内,登录或使用了某个产品的用户数(去除重复登录的用户); - MAU 月活: 月活跃用户数量(Monthly Active User,MAU)
月活跃用户数量通常统计一个月(统计月)之内,登录或使用了某个产品的用户数(去除重复登录的用户); - PV(Page View):页面浏览量 指网站页面被访问的总次数。用户每打开一个页面就会被记录一次 PV,多次打开同一页面则累计计数。例如,一个用户在一天内访问了网站的首页 5 次,那么这个首页在这一天的 PV 就是 5。
- UV(Unique Visitor) - 独立访客: 指在一定时间范围内访问网站的不同用户的数量。同一用户无论访问网站多少次,在统计周期内只计算一次 UV。例如,在一天内,用户 A 访问了网站 10 次,用户 B 访问了网站 3 次,那么这一天的 UV 就是 2。注意,DAU 是 UV 的一个子集。因为 DAU 强调的是在一天内有活跃行为的用户,而 UV 只是统计了不同的访问者,这些访问者不一定在当天有实际的活跃行为。
Note:日活、月活反映用户的活跃度,但是无法反映用户的粘性。
日活、PV、UV数据统计的特点
- 数据需要去重;
- 数据允许有一定的偏差,101W和102W差距不大;
- 占用空间尽可能小;
HyperLogLog是Redis的高级数据结构,是统计基数(如日活、PV、UV)的利器。
在介绍HyperLogLog的原理之前,请你先来思考一下,如果让你来统计基数,你会用什么方法。
使用 redis Set 进行基数统计
使用 redis Set 进行基数统计的方法是:只需要把数据都存入Set,然后用scard命令就可以得到结果,这是一种思路,但是存在一定的问题。
import redis.clients.jedis.Jedis;
public class RedisSetCardinalityDemo {
public static void main(String[] args) {
// 连接到Redis服务器
Jedis jedis = new Jedis("localhost", 6379);
// 假设要统计用户的访问次数,这里模拟添加用户ID到Set中
String setKey = "visited_users";
// 添加一些用户ID到Set中
jedis.sadd(setKey, "user1", "user2", "user2", "user3", "user4", "user4", "user4");
// 获取Set的基数,即不同元素的数量
long cardinality = jedis.scard(setKey);
System.out.println("基数统计结果:不同元素的数量为 " + cardinality);
// 关闭Redis连接
jedis.close();
}
}
在上述代码中:
- 定义了一个 Set 的键名
visited_users,用于模拟统计访问过的用户情况。 - 使用
sadd方法向 Set 中添加了多个用户 ID,注意其中有重复的 ID,这正是要通过基数统计来确定不同用户数量的场景。 - 最后通过
scard方法获取 Set 的基数,也就是不同元素(这里即不同用户)的数量,并将结果输出。
通过这样的方式,就可以利用 Redis Set 数据结构简单地实现基数统计功能。
使用 redis Set 进行基数统计的问题:
如果数据量非常大,那么将会耗费很大的内存空间,尤其是如果日活一个亿,那么这个是一个超级大的set(100M * 4), 是一个超级大的bigkey。
如果这些数据仅仅是用来统计基数,那么无疑是造成了巨大的浪费,并且也是非常的低性能,因此是,我们需要找到一种占用内存较小的方法。
使用 redis bitmap 进行基数统计
bitmap同样是一种可以统计基数的方法,可以理解为用bit数组存储元素,例如01101001,表示的是[1,2,4,8],bitmap中1的个数就是基数。
以下是一个使用 Redis 的 Bitmap 进行日活统计的 Java 示例代码:
import redis.clients.jedis.Jedis;
public class RedisBitmapDailyActiveUsersDemo {
public static void main(String[] args) {
// 连接到Redis服务器
Jedis jedis = new Jedis("localhost", 6379);
// 定义存储日活用户的Bitmap键名,格式可以是 "daily_active_users:日期",这里假设日期为20241112
String bitmapKey = "daily_active_users:20241112";
// 模拟用户ID,这里简单用整数表示,实际应用中可能是更复杂的用户唯一标识
int[] userIds = {1001, 1002, 1003, 1004, 1005};
// 将每个用户ID对应的位设置为1,表示该用户当天活跃
for (int userId : userIds) {
// 使用SETBIT命令,将用户ID对应的位设置为1
jedis.setbit(bitmapKey, userId, true);
}
// 统计日活用户数量,使用BITCOUNT命令
long dailyActiveUsersCount = jedis.bitcount(bitmapKey);
System.out.println("日活用户数量为: " + dailyActiveUsersCount);
// 关闭Redis连接
jedis.close();
}
}
在上述代码中:
- 定义了一个用于存储日活用户的 Bitmap 键名,这里按照
daily_active_users:日期的格式进行定义,示例中假设日期为20241112。 - 模拟了一些用户 ID,这里简单用整数表示,实际情况中应该是能唯一标识用户的信息。
- 然后通过循环,使用
SETBIT命令,将每个用户 ID 对应的位在 Bitmap 中设置为 1,表示该用户当天活跃。 - 最后使用
BITCOUNT命令,统计 Bitmap 中值为 1 的位的数量,也就是日活用户的数量,并将结果输出。
通过这样的方式,就可以利用 Redis 的 Bitmap 数据结构方便地实现日活统计功能。
在实际应用中,可以根据具体需求进一步扩展和优化代码,比如从真实的用户访问日志中提取用户 ID,或者结合其他数据进行更深入的分析等。
bitmap也可以轻松合并多个集合,只需要将多个数组进行异或操作就可以了。
Bitmaps可用于统计日活吗?
Bitmaps 在大数据下的应用,那么Bitmaps可以用于统计日活数据吗?我们来做个计算分析(以一亿用户为例):
| 统计方式 | 占用计算 | 1亿用户占用空间(M) |
|---|---|---|
| Redis 32bit的string数据类型 | 1个string大概所需存储空间为4字节,可存储32 bit位 | 10^8 / (1024 * 1024 * 8 / 32) ≈ 381 M |
| Redis Bitmaps | Bitmaps单个支持512M,不像int单个仅存储32位 | 10^8 / (1024 * 1024 * 8) ≈ 12M |
bitmap相比于Set也大大节省了内存,我们来粗略计算一下,统计1亿个数据的基数,需要的内存是:100000000/8/1024/1024 ≈ 12M。
虽然bitmap在节省空间方面已经有了不错的表现,和set(100M * 4)相比,空间的消耗 缩小了 400倍。
当然,使用Bitmaps计算日活月活,还有很多优势的地方:
- 计算日活:bitcount key获取key为1的数量;
- 计算月活:可把30天的所有bitmap做or计算,再进行bitcount计算;
- 计算留存率:昨日留存=昨天今天连续登录的人数/昨天登录的人数,即昨天的bitmap与今天的bitmap进行and计算,再除以昨天bitcount的数量。
通过以上计算,统计一个小型(10W用户)网站的日活已不在话下,我们发现Bitmaps已经很节省空间了。
但是大型互联网公司的日活、UV、PV,一个set如果上100M,这个就太浪费,而且也性能太低了。
怎么才能性能高点呢?
使用 HyperLogLog进行基数统计
以下是一个使用 Redis HyperLogLog 进行日活统计的 Java 示例代码:
import redis.clients.jedis.Jedis;
public class RedisHyperLogLogDailyActiveUsersDemo {
public static void main(String[] args) {
// 连接到Redis服务器
Jedis jedis = new Jedis("localhost", 6379);
// 定义存储日活用户的HyperLogLog键名,格式可设为 "HLL:日期",这里假设日期为20241112
String hyperloglogKey = "HLL:20241112";
// 模拟用户ID,实际应用中可能是从用户访问日志等获取真实的用户唯一标识
int[] userIds = {1001, 1002, 1002, 1003, 1004, 1004, 1004};
// 将每个用户ID对应的信息添加到HyperLogLog中,以统计日活
for (int userId : userIds) {
// 使用PFADD命令将用户ID添加到HyperLogLog结构中
jedis.pfadd(hyperloglogKey, String.valueOf(userId));
}
// 获取日活用户的基数估计值,即不同用户的数量估计
long dailyActiveUsersCount = jedis.pfcount(hyperloglogKey);
System.out.println("日活用户数量估计值: " + dailyActiveUsersCount);
// 关闭Redis连接
jedis.close();
}
}
在上述代码中:
- 定义了一个用于存储日活用户的 HyperLogLog 键名,按照
HLL:日期的格式进行定义,示例中假设日期为20241112。 - 模拟了一些用户 ID,这里简单用整数表示,实际情况应从真实的用户访问日志等获取能唯一标识用户的信息。
- 然后通过循环,使用
PFADD命令将每个用户 ID 对应的信息添加到 HyperLogLog 结构中,以此来统计日活用户。 - 最后使用
PFCOUNT命令获取 HyperLogLog 的基数估计值,也就是日活用户数量的估计值,并将结果输出。
通过这样的方式,就可以利用 Redis 的 HyperLogLog 数据结构方便地实现日活统计功能。
亿级用户日活统计,HyperLogLog 的空间消耗是多大呢?
使用 Redis 统计集合的基数一般有三种方法,分别是使用 Redis 的 HashMap,BitMap 和 HyperLogLog。
前两个数据结构在集合的数量级增长时,所消耗的内存会大大增加,但是 HyperLogLog 则不会。
Redis 的 HyperLogLog 通过牺牲准确率来减少内存空间的消耗,只需要12K内存,在标准误差0.81%的前提下,能够统计2^64个数据。
所以 HyperLogLog 是否适合在比如统计日活月活此类的对精度要不不高的场景。
网上有小伙伴进行过对比实验,分别插入一万数字和一千万数字,三种数据结构消耗的内存统计如下所示。
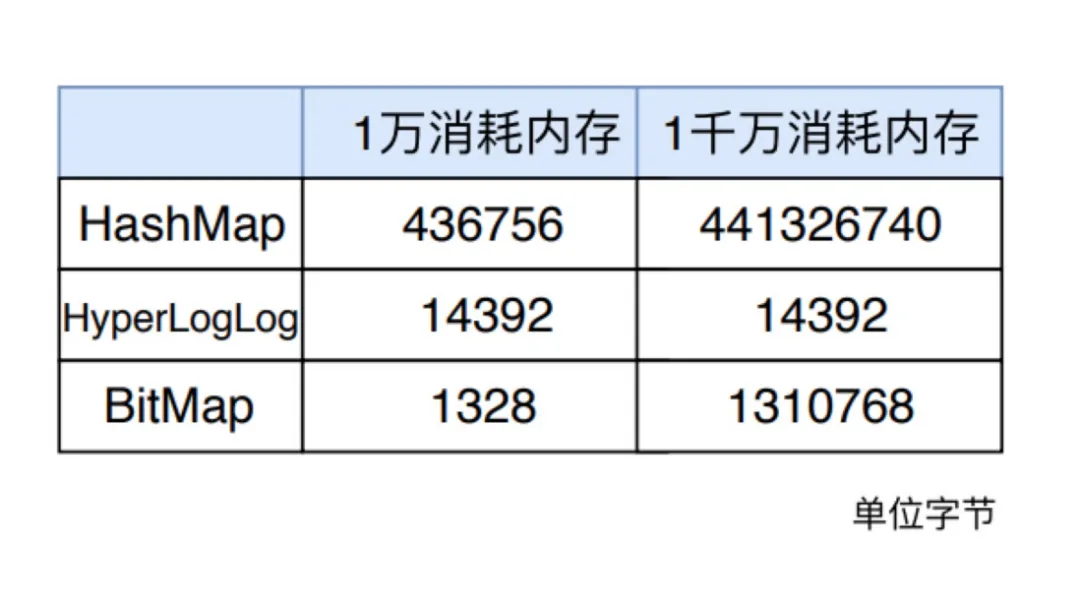
从表中可以明显看出,一万数量级时 BitMap 消耗内存最小, 一千万数量级时 HyperLogLog 消耗内存最小,但是总体来看,HyperLogLog 消耗的内存都是 14392 字节,可见 HyperLogLog 在内存消耗方面有自己的独到之处。
亿级用户场景,HyperLogLog将会出来拯救我们,HyperLogLog 的大小,还是 12KB, 因为 12KB的HyperLogLog 最大可以统计到 2的50次方的大小规模。
所以 HyperLogLog 拯救了我们。 当然 ,HyperLogLog的结果并不精准,错误率大概在0.81%。
HyperLogLog的基本用法
HyperLogLog是Redis的高级数据结构,它在做基数统计的时候非常有用,每个HyperLogLog的键可以计算接近264不同元素的基数,而大小只需要12KB。
HyperLogLog的基本用法 主要是 HyperLogLog的三个命令,PFADD、PFCOUNT、PFMERGE。
HyperLogLog三个命令
【HyperLogLog核心命令】:PFADD、PFCOUNT、PFMERGE;
| 命令 | 功能 | 参数 |
|---|---|---|
| PFADD | 添加元素到HLL数据结构 | key element [element …] |
| PFCOUNT | 返回HLL的基数值 | key [key …] |
| PFMERGE | 合并多个HLL结构数据到destkey | destkey sourcekey [sourcekey …] |
HLL操作命令中的PF含义:HyperLogLog 数据结构的发明人 Philippe Flajolet 的首字母缩写。
我们先来逐一介绍一下。
PFADD
最早可用版本:2.8.9
时间复杂度:O(1)
将参数中的元素都加入指定的HyperLogLog数据结构中,这个命令会影响基数的计算。
如果执行命令之后,基数估计改变了,就返回1;否则返回0。
如果指定的key不存在,那么就创建一个空的HyperLogLog数据结构。
该命令也支持不指定元素而只指定键值,如果不存在,则会创建一个新的HyperLogLog数据结构,并且返回1;否则返回0。
PFCOUNT
最早可用版本:2.8.9
时间复杂度:O(1),对于多个比较大的key的时间复杂度是O(N)
对于单个key,该命令返回的是指定key的近似基数,如果变量不存在,则返回0。
对于多个key,返回的是多个HyperLogLog并集的近似基数,它是通过将多个HyperLogLog合并为一个临时的HyperLogLog,然后计算出来的。
HyperLogLog可以用很少的内存来存储集合的唯一元素。(每个HyperLogLog只有12K加上key本身的几个字节)
HyperLogLog的结果并不精准,错误率大概在0.81%。
需要注意的是:该命令会改变HyperLogLog,因此使用8个字节来存储上一次计算的基数。所以,从技术角度来讲,PFCOUNT是一个写命令。而多数PFADD命令不会更新寄存器,PFCOUNT 才进行 基数统计 ,这样PFADD 才可以达到每秒上百次请求的效果。不过,虽然PFCOUNT慢,但是 PFCOUNT会缓存上一次结算的基数结果。
PFMERGE
最早可用版本:2.8.9
时间复杂度:O(N),N是要合并的HyperLogLog的数量
用法:PFMERGE destkey sourcekey [sourcekey …]
PFMERGE 合并多个HyperLogLog,合并后的基数近似于合并前的基数的并集(observed Sets)。计算完之后,将结果保存到指定的key。
PFMERGE 将多个 HyperLogLog 合并为一个 HyperLogLog , 合并后的 HyperLogLog 的基数接近于所有输入 HyperLogLog 的并集基数。
比如,合并当月的所有日活数据,合并成为月活:
PFMERGE HLL:20241110 … HLL:20241129 HLL:20241130 HLL:20241131
使用 HyperLogLog进行 统计网站日活月活
日活:每天一个HLL,用户登录时则 PFADD HLL:20241112 userID;
月活:合并当月的所有日活数据,PFMERGE HLL:20241110 … HLL:20241129 HLL:20241130 HLL:20241131
HyperLogLog命令示例
127.0.0.1:6379> pfadd hll 1
(integer) 1
127.0.0.1:6379> pfadd hll 1
(integer) 0
127.0.0.1:6379> pfadd hll 2 3 4
(integer) 1
127.0.0.1:6379> pfcount hll
(integer) 4
127.0.0.1:6379> pfcount hll:notexist
(integer) 0
127.0.0.1:6379> pfadd hll2 a b
(integer) 1
127.0.0.1:6379> pfcount hll2
(integer) 2
127.0.0.1:6379> pfcount hll hll2
(integer) 6
127.0.0.1:6379> get hll
"HYLL\x01\x00\x00\x00\x04\x00\x00\x00\x00\x00\x00\x00A\xee\x84[v\x80Mt\x80Q,\x8cC\xf3"
127.0.0.1:6379> set hll:error error666
OK
127.0.0.1:6379> pfcount hll:error
(error) WRONGTYPE Key is not a valid HyperLogLog string value.
加入元素、合并hyll结构:
127.0.0.1:6379> pfadd hllm1 1 2 3 4 5
(integer) 1
127.0.0.1:6379> pfadd hllm2 5 6 7 8
(integer) 1
127.0.0.1:6379> pfmerge hllm3 hllm1 hllm2
OK
127.0.0.1:6379> pfcount hllm3
(integer) 8
127.0.0.1:6379> pfadd hllm4 7 8 9 10 11 12 14 14
(integer) 1
127.0.0.1:6379> pfmerge hllm4 hllm1 hllm2
OK
127.0.0.1:6379> pfcount hllm4
(integer) 13
HyperLogLog 、Sets命令对比分析
HyperLogLog虽然技术实现是一种 不同的数据结构,但底层依旧是Redis strings,所以可以使用GET命令获取序列化后的数据,使用SET命令反序列化数据存储到Redis。
HyperLogLog和Sets的区别
| 对比/数据类型 | Sets | HyperLogLog |
|---|---|---|
| 是否实际存储统计元素 | 存储 | 不存储元素,仅存储存在的标记 |
| 增加元素 | SADD | PFADD |
| 统计元素数量 | SCARD | PFCOUNT |
| 删除元素 | SREM | 不支持删除元素 |
| 合并 | PFMERGE |
HyperLogLog 使用的注意事项
HyperLogLog(HLL)是一种用于基数计算的概率数据结构,通俗的说就是支持集合中不重复元素的统计。
常规基数计算需要准备一块内存空间用于存储已经计数的元素,避免某些元素被重复统计。
Redis提供了一种用精度来换取内存空间的算法,标准误差低于1%。
HLL 12kb内存可计算接近 2^64 个不同元素的基数。仅需要12K 就能完成统计(再加上HLL自身所需的一点bytes),如果HyperLogLog中的元素较少,所需内存空间更小。
HyperLogLogs的标准误差是0.81%。
输入元素数量或体积非常大时,HLL所需空间固定且很小。
HyperLogLog命令注意事项
- PFADD仅存储标记,不存储元素本身;
- PFCOUNT实际是一个write命令,执行PFCOUNT时可能会重新计算计数值并存储;
- key有多个时,PFCOUNT会动态合并计算,并且计算结果不会被缓存,所以生产环境执行PFCOUNT时尽量避免带多个key;
- key有多个时,PFCOUNT是先合并再计算,结果为多个对象合并<去重>后的基数值(注意:不是基数值之和);
- PFMERGE计算的是sourcekey的并集;
- 如果destkey已存在,则PFMERGE执行后destkey最终的结果是dest+source的并集;
HyperLogLog原理
HyperLogLog 数学原理 : 极大似然估计 和 伯努利实验
HyperLogLog 的数学原理比较复杂, 全网的文章都讲得模模糊糊,似懂非懂。
这里,尼恩 给大家来一个 浅显易懂的介绍, 全网第一次。
其使用的数学原理是统计学中的极大似然估计。
这种通过大量结果反向估计条件的数学方法就是极大似然估计。
场景1: 大概率 事件的原理
现在A 、B口袋都装有100个球:
- A口袋中是99个白球1个黑球
- B口袋中是99个黑球1个白球。
当我们随机挑选一个口袋,然后从中拿出一个球。
- 如果拿出的球是 白色的,那么我们可以说“大概率”我们取出的是A口袋。
- 如果拿出的球是 黑色的,那么我们可以说“大概率”我们取出的是B口袋。
这种“大概率” 就是“极大似然估计”的思想。 当然, 数学有一套自己的形式, 咱们就不是深究了。
场景2:正向的推测
假设一个 口袋,其中99个白球,1个黑球。
什么是 正向的推测? 就是知道了条件(99个白球,1个黑球),从而推测出结果(取出任意一个球,是白球的概率为99%)。
很容易我们就可以得出结论,从中取出任意一个球,是白球的概率为99%,是黑球的概率为1%。
但这只是理论上的推测,实际取球100次,每次都放回,那么是白球的比例可能为90%(并不是99%),黑球的比例可能为10%(并不是1%) 。
但是,当我们取球的次数越多,实际情况将越符合理论情况,是白球的概率为99%,是黑球的概率为1%。
场景3: 反向的推测
假设一个 口袋放了100个球,我们不知道黑球多少,白球多少。
什么是反向的推测?通过 观察 结果(取10000次球,9900次是白球,100次是黑球) ,可以推测出条件(99个白球,1个黑球)。
当我们取球10000次的时候,其中9900次是白球,100次是黑球,此时我们就可以大概率确定A口袋中是99个白球,而这种确定程度随着我们实际取球次数的增加也将不断增加。
无论是正向推测或是反向推测,只有当执行操作的次数足够多的时候,才能使得实际情况更接近理论推测。
伯努利实验 与 通过二进制位中的位信息来估计基数
伯努利实验, 尼恩在刚开始学习概率统计的时候,也觉得这是一个头疼的名词, 当时被这个名字唬住了。
现在想来, 这个其实很简单。
伯努利实验其实就是扔硬币实验。
场景1:正向推测
扔一次硬币 得到正面或反面的可能性是相同的,都是50%。所以,按照原始的极大似然估计的思想, 我们扔10000次硬币,那么大概率是接近5000次正面,5000次反面。
在伯努利实验( 扔硬币实验)中,我们要根据 扔出去硬币的 次数条件, 要正向推测 全面硬币为正面的概率结果。
-
如果我们扔2次硬币, 2次都是正面 的概率为1/4。
-
如果我们扔10次硬币呢, 10次都是正面 的 概率为1/1024。
-
扔100次硬币 , 可能10次都是正面 ,概率为 1/(2^100)。
-
假如扔了n次,那么n次都是正面的概率为 1/(2^n )。
现在,调整一下扔硬币规则:不断扔硬币,直到出现反面朝上,此时记录下扔硬币的总次数。
注意:如果是正面朝上,那么就继续扔。
例如:
- 抛了5次硬币,前4次都是正面朝上,第5次是反面朝上,我们就记录下次数5,概率为1/(2^5),就是 1/32。
- 扔10次硬币 ,前9次都是正面朝上,第10次是反面朝上,概率为1/1024。
- 假如扔了n次,那么n-1次都是正面的概率为,第n次是反面朝上,概率为 1/(2^n)。
场景2:反向推测
反向推测就是 即根据 结果(发生了一次 概率 结果为 1/32),推测条件( 做了几次扔硬币实验,32次) 。
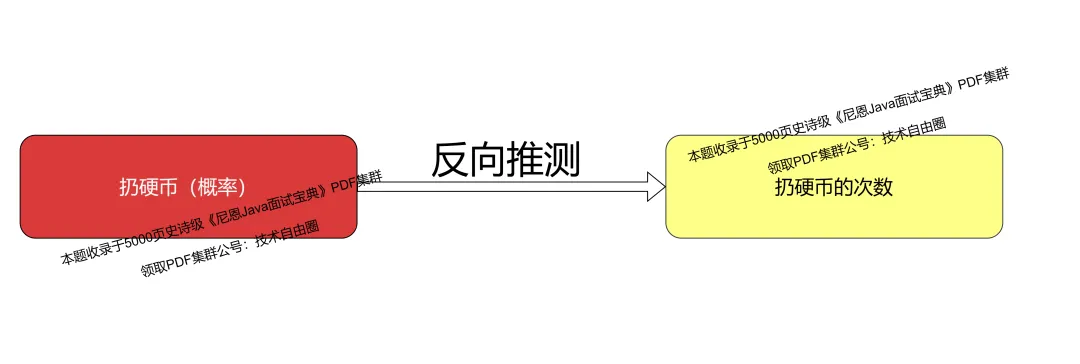
反向推测,如果一个结果发生的概率是1/32,那么我们大体上就需要做32次同样的事情才能得到这个结果。
例如:
-
抛硬币实验,前4次都是正面朝上,第5次是反面朝上的概率是 1/32, 我们如果要实现这个结果,条件是 需要抛出 32次硬币。
-
抛硬币实验,前9次都是正面朝上,第10次是反面朝上的概率是1/1024, 我们如果要实现这个结果,条件是 需要抛出 1024 次硬币。
-
抛硬币实验,前n-1次都是正面朝上,第n次是反面朝上的概率是1/(2^n), 我们如果要实现这个结果,条件是 需要抛出2^n次硬币。
伯努利过程的总结
伯努利过程就是一个抛硬币实验的过程。
抛一枚正常硬币,落地可能是正面,也可能是反面,二者的概率都是 1/2 。
伯努利过程就是一直抛硬币,直到落地时出现正面位置,并记录下抛掷次数k。
比如说,抛一次硬币就出现正面了,此时 k 为 1; 第一次抛硬币是反面,则继续抛,直到第三次才出现正面,此时 k 为 3。
对于 n 次伯努利过程,我们会得到 n 个出现正面的投掷次数值 k1, k2 ... kn , 其中这里的最大值是k_max。
根据 反向推测,我们可以得出一个结论: 2^{k_max} 来作为n的估计值。
也就是说, 可以根据最大投掷次数,近似的推算出进行了几次伯努利过程。
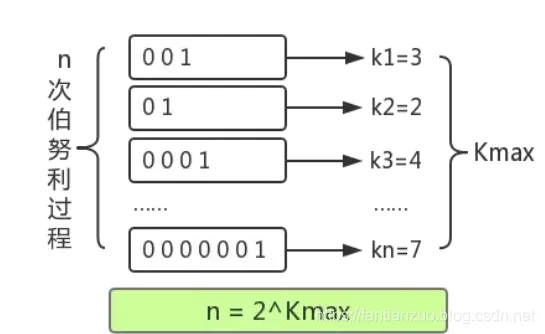
HyperLogLog 与 扔硬币实验反向推测的原理
关键的地方来了。
HyperLogLog 的数学原理比较复杂, 全网的文章都讲得模模糊糊,似懂非懂。这里,尼恩第一次给大家来一个 浅显易懂的介绍。
关键就在这里。
HyperLogLog 通过统计哈希值二进制位 信息(概率) 来估计集合基数(类似也就是扔硬币的次数),实际上就是上面的反向推测:
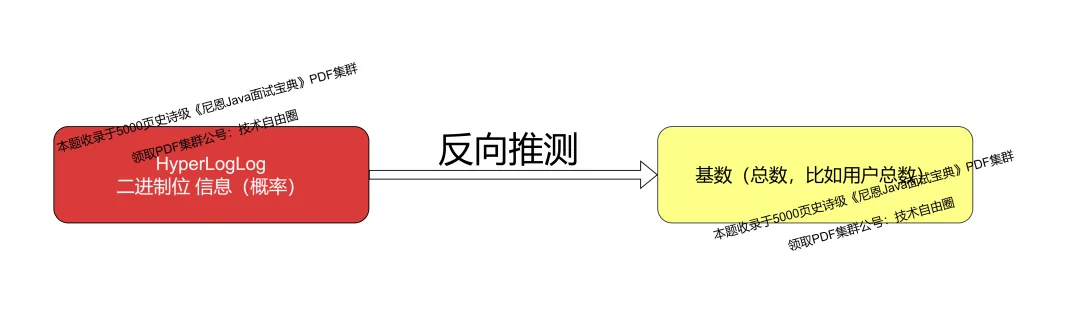
HyperLogLog 的原理,就是经典的反向推测。
HyperLogLog 使用hash算法完成 伯努利试验(/ 扔硬币)
在伯努利试验的实验有3个特点:
1.硬币只有正反两面。
2.硬币正反面出现的概率相同。
3.单次实验需要投掷多次硬币。
HyperLogLog 的 概率信息 如何模拟 扔硬币呢?通过 hash算法得到一个 哈希值,把这个哈希值看做是一个扔硬币的概率值。
或者说,哈希值看作是一系列的伯努利实验。将哈希值每个二进制位是否为 1 看作是一次伯努利实验(1 代表成功,0 代表失败)。从右边开始,第一个为1的bit出现的位数,相当于概率。
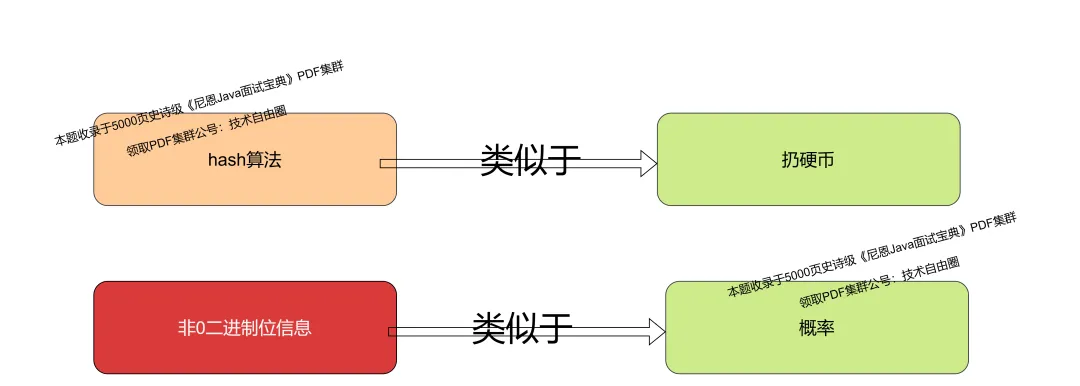
有了这个概率(HyperLogLog 通过统计哈希值二进制位 信息), 就可以反向推测, 来估计集合基数(类似也就是扔硬币的次数):

-
从右边开始,第一个为1的bit出现的位数是第5位,相当于 第5次是反面朝上的概率是 1/32, 我们如果要实现这个结果,条件是 需要抛出 32次硬币, 集合基数为 32 。
-
从右边开始,第一个为1的bit出现的位数是第10位,相当于第10次是反面朝上的概率是1/1024, 我们如果要实现这个结果,条件是 需要抛出 1024 次硬币, 集合基数为 1024 。
-
从右边开始,第一个为1的bit出现的位数是第n位,相当于第n次是反面朝上的概率是1/(2^n), 我们如果要实现这个结果,条件是 需要抛出2^n次硬币, 集合基数为 2^n。
-
从右边开始,第一个为1的bit出现的位数是第40位,相当于第40次是反面朝上的概率是1/(2^40), 我们如果要实现这个结果,条件是 需要抛出2^40次硬币, 集合基数为 2^40。
看到这里,大家对HyperLogLog 和 伯努利试验(/ 扔硬币)关系,就彻底的不懵懵懂懂,迷迷糊糊了。终于把大家从把大家从迷迷瞪瞪、模模糊糊的梦境解脱出来。

说句题外话,依托于20年+技术内功, 尼恩团队 经常性的、把复杂的问题做清晰深入的穿透式、起底式的分析:
- 比如 Netty的内存池和对象池
- 比如DDD的建模和落地,
- 比如Caffeine的底层架构,
- 比如高性能葵花宝典
- 比如 Thread Local 学习圣经
等等等等。上面的很多难点, 超级难, 超级难,其实穷其一生,很多人 都搞 懂, 尼恩团队用深厚的 技术内功,给大家把难题化解了。 具体,请参见尼恩的 各种技术圣经 PDF。
HyperLogLog 使用hash算法 扔硬币演示
如果 要统计 用户的个数,我们可以对 用户id进行 hash。
假设:哈希值是一个 二进制序列, 从右往左, 正好可以满足这3个条件:
1.hash结果的每一个bit只有0和1,代表硬币的正反两面。
2.如果hash算法足够好,得到的结果就足够随机,可以近似认为,每一个bit的0和1产生的概率是相同的。
3.hash的结果如果是64个bit,正好代表最多可以投掷了64次硬币。
因此执行一次hash,就相当于完整地进行了一次场景3中的投币实验。按照约定,实验完成后,我们需要记录硬币投掷的结果。
假定现在有2个用户id;user1、user2
先对user1进行hash,假定得到如下8个bit的结果:
10100100
此时从右到左,我们约定0表示反面,1表示正面。
于是在这次实验中,第一个为1的bit出现在第三位,相当于先投出了2次反面,然后投出1次正面,于是我们记录下这次实验的投掷次数为3。
因为约定了:只要投出正面,当次实验就结束。所以, 第一个1左边的所有bit就不再考虑了。
再对user2进行hash,假定得到:
01101000
第一个为1的bit出现在第4位,于是记录下4。
对于每个用户的访问请求,我们都可以对用户的id进行hash,那么通过记录到的位数的最大值,把这个值作为 概率值, 然后进行反向的 推测。
例如某个页面有n个用户进行了访问, 发现记录下的 左边全0时第一个为1的bit出现位数的最大值10 ,而这种情况发生的概率为1/1024,于是反向推测,可以推测大概有1024个用户访问过该页面,才有可能出现一次这种结果
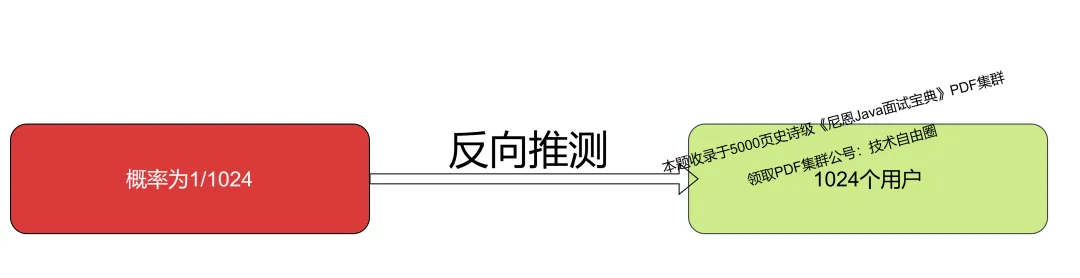
我们就可以大概估计出一共进行了多少次实验(相当于场景3中的反向推测),也就是有多少个不同的用户发生了访问。
总之,在统计不同元素数量的过程中,HyperLogLog 利用了这种类似伯努利实验的特性来估算基数。
这个过程实际上是在寻找最有可能产生观察到的哈希值分布的基数估计值。
例如,通过对每个桶中的数据进行分析,找到一个能最大程度地符合观察到的哈希值模式的基数估计,这类似于极大似然估计中寻找使样本出现概率最大的参数的过程。
这就非常符合hyperloglog的特点,只有当数据量足够大的时候,误差才会足够小。
因此极大似然估计的本质就是:当能观察的结果数量足够多时,我们就可以大概率确定产生相应结果所需要的条件的状态。
HyperLogLog 的底层数据结构
HyperLogLog 是一种概率数据结构,它使用概率算法来统计集合的近似基数。而它算法的最本源则是伯努利过程。
这些比特串就类似于一次抛硬币的伯努利过程。比特串中,0 代表了抛硬币落地是反面,1 代表抛硬币落地是正面,如果一个数据最终被转化了 10010000,那么从低位往高位看,我们可以认为,这串比特串可以代表一次伯努利过程,首次出现 1 的位数为5,就是抛了5次才出现正面。
HyperLogLog 在添加元素时,会通过Hash函数模拟 抛硬币,将元素hash后,转为64位比特串, 概率信息出自于这个里边的 第一个非 0位的编号。
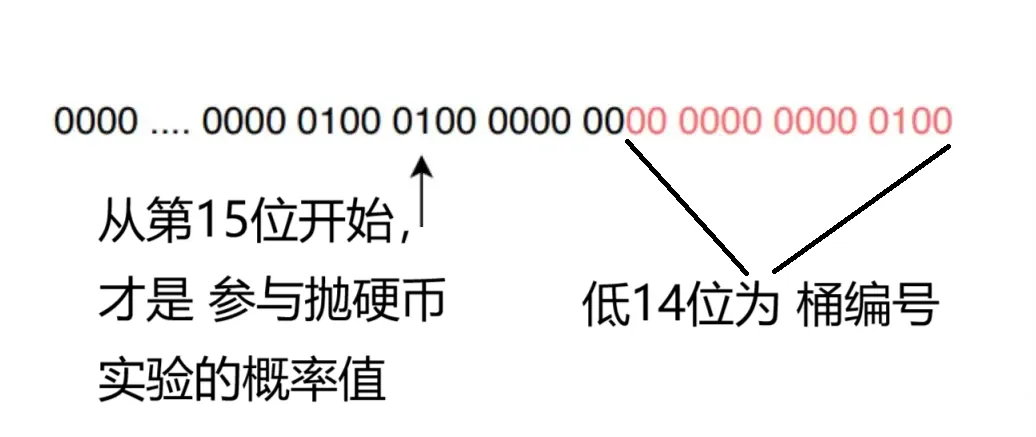
比如,hash之后的转为64位比特串 如下:

那么,第一个 非0位(概率位)为3吗?并不是。
HyperLogLog 用的并不是这个 非0位,而是用低14位作为桶的编号。
从第15位开始的进行计算,第一个 非0位(概率位)才是参与抛硬币实验的概率位,比如下面的这个位:
为什么 HyperLogLog 有分桶的概念呢?
HyperLogLog 在添加元素时,会通过Hash函数,将元素转为64位比特串,例如输入5,便转为101(省略前面的0,下同)。
前面讲到, HyperLogLog 的基本思想是利用概率位的最大值,反向推测,预估整体基数。但是这种预估方法存在较大误差,为了改善误差情况,HyperLogLog中引入分桶平均的概念,计算 m 个桶的调和平均值。
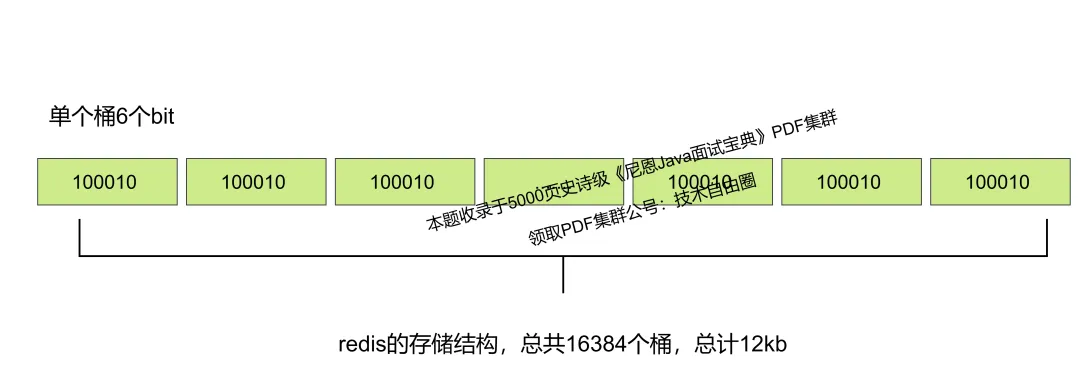
Redis 中 HyperLogLog 一共分了 2^14 个桶, 用 hash的低14位作为编号 , 最大的编号是16383, 也就是 16384 个桶。
Redis HyperLogLog 对于一个输入的字符串,首先得到64位的hash值,用前14位来定位桶的位置(共有 2^14 ,即16384个桶)。
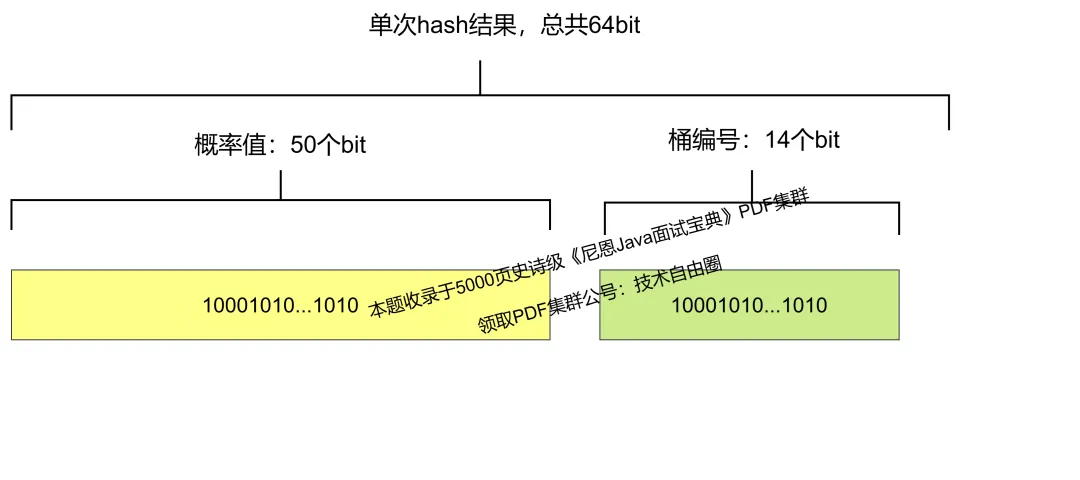
64位的hash值 剩下的高位有50位,即为伯努利过程,最大的 非0位为编号为50,使用6位二进制可以记录下来,因为最大的6位二进制可以记录到64。
所以, 每一个桶的 概率位(从右边开始的非0位)的编号,最多 6个二进制位就可以 保留下来了。 每一个桶的 的大小就是 6个二进制位。
每个桶有6bit,记录第一次出现1的位置count,当然,如果同一个桶的新的概率位变大了,如果count>oldcount,就用count替换oldcount。
HyperLogLog中引入分桶平均的概念,计算 16384 个桶的调和平均值。 调和平均值的计算公式如下:
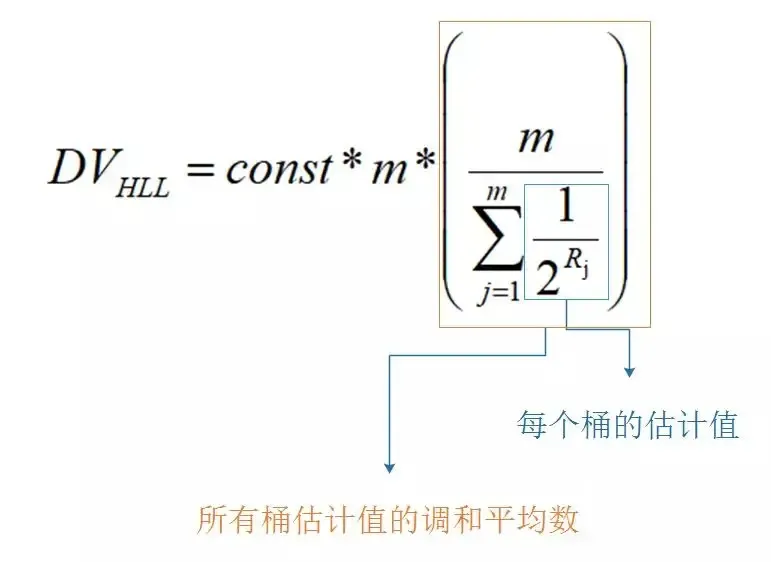
其中m是桶的数量, p=log2m。
const是修正常数,它的取值会根据m而变化。
switch (p) {
case 4:
constant = 0.673 * m * m;
case 5:
constant = 0.697 * m * m;
case 6:
constant = 0.709 * m * m;
default:
constant = (0.7213 / (1 + 1.079 / m)) * m * m;
}
HyperLogLog 的Redis 源码分析
我们首先来看一下 HyperLogLog 对象的定义
struct hllhdr {
char magic[4]; /* 魔法值 "HYLL" */
uint8_t encoding; /* 密集结构或者稀疏结构 HLL_DENSE or HLL_SPARSE. */
uint8_t notused[3]; /* 保留位, 全为0. */
uint8_t card[8]; /* 基数大小的缓存 */
uint8_t registers[]; /* 数据字节数组 */
};
hllhdr 是一个自定义的结构体 , 是用于实现 HyperLogLog 算法相关的数据结构。
hllhdr 包含了用于存储 HyperLogLog 对象各种属性的成员变量,这些属性对于正确地实现 HyperLogLog 的功能(如基数估计)非常关键。成员变量详细介绍
-
magic[4]这是一个长度为 4 的字符数组,用于存储魔法值(Magic Number)。
在这里,魔法值被定义为
"HYLL"。魔法值的主要作用是在程序运行过程中,用于识别数据结构的类型, 尤其是从 文件中进行 hyll 结构的反序列化的场景。
当读取数据时,通过检查这个魔法值,可以快速确定数据是否是期望的 HyperLogLog 结构。
例如,在从存储介质(尤其是文件)中读取数据时,如果前 4 个字节不是
"HYLL",就可以判断数据可能损坏或者不是 HyperLogLog 结构的数据。 -
encoding这是一个
uint8_t类型(无符号 8 位整数)的变量。它用于指示 HyperLogLog 数据结构是密集型(
HLL_DENSE)还是稀疏型(HLL_SPARSE)类型。这种区分很重要,因为 HyperLogLog 在不同的数据分布和规模下,可能会采用不同的内部存储方式来优化空间和计算效率。
在密集型结构中,数据的存储和处理方式可能更偏向于紧凑和高效的数组形式;
而在稀疏型结构中,可能会采用更节省空间的方式来存储相对较少的元素信息,以适应元素数量较少或者分布比较特殊的情况。
-
notused[3]这是一个长度为 3 的
uint8_t数组,被标记为保留位(Reserved Bits),并且全部初始化为 0。这些保留位的存在通常是为了未来可能的扩展或者结构调整。
在当前版本的定义中,它们没有被使用,但在对数据结构进行升级或者修改时,可以利用这些位来添加新的功能或者属性,而不会破坏现有的数据兼容性。
-
card[8]这是一个长度为 8 的
uint8_t数组 ,总计 64位,用于缓存基数(Cardinality)的大小。基数是 HyperLogLog 算法的一个核心概念,它用于估计集合中不同元素的数量。
通过缓存基数,可以在某些操作中快速获取估计值,而不需要重新计算整个 HyperLogLog 数据结构。
这种缓存机制有助于提高频繁查询基数操作的效率, 不需要每次都进行计算。
例如,在需要多次统计集合中不同元素数量的应用场景中,直接从
card数组中读取缓存的估计值可以节省计算时间。 -
registers[]这是一个字节数组,用于存储实际的数据 。
具体存储的数据内容和格式取决于
encoding所指示的结构类型(密集型或稀疏型)。在密集型结构中,这些寄存器可能以一种紧密排列的方式,存储元素的哈希信息的 概率位信息,用于基数估计的计算;
在稀疏型结构中,存储方式进行 了相邻概率位 的压缩,以适应较少元素的情况。
这些寄存器是 HyperLogLog 算法进行基数估计的关键部分,通过对寄存器中的数据进行分析和计算,可以得出集合中不同元素数量的估计值。
HyperLogLog 的 密集存储结构
HyperLogLog 对象中的 registers 数组就是桶,它有两种存储结构,分别为密集存储结构和稀疏存储结构,两种结构只涉及存储和桶的表现形式,从中我们可以看到 Redis 对节省内存极致地追求。
HyperLogLog 的 密集存储结构 的图如下:

HyperLogLog 的 密集存储结构,它也是十分的简单明了,registers[] 有 2^14 (16384 )个 6 bit的桶,使用 uint8_t 字的数组去存储, 大概12KB的字节数组, 因为字节有 8 位,而桶只需要 6 位, 所以可以存放 16384 个桶。
redis 对16384 (2的14次方)非常的热衷?
来看 哈希空间划分:Redis 集群预先分配了 16384 个哈希槽。每个键(key)通过 CRC16 算法计算出一个 16 位的哈希值,然后将这个哈希值对 16384 取模,得到这个键所属的哈希槽编号。
例如,对于一个键值对{key: "user:123", value: "John"},先计算key的哈希值,假设通过 CRC16 算法得到哈希值为h,那么该键所属的哈希槽编号为h % 16384, 对应到redis 的集群分片。
HyperLogLog 的 稀疏存储结构
是不是创建一个 HyperLogLog ,就一定需要 12kb呢?
redis 感觉这样子的话,太浪费了。
于是有了HyperLogLog 的稀疏存储结构。HyperLogLog 的稀疏存储结构是为了节约内存消耗。‘ HyperLogLog 数据结构是密集型(HLL_DENSE)还是稀疏型(HLL_SPARSE)类型,前面讲了,有个专门的属性去标识。
SPARSE 类型 不像DENSE 密集存储模式一样,真正找了那么多个字节数组来表示2^14 个桶,而是使用特殊的压缩结构来表达。
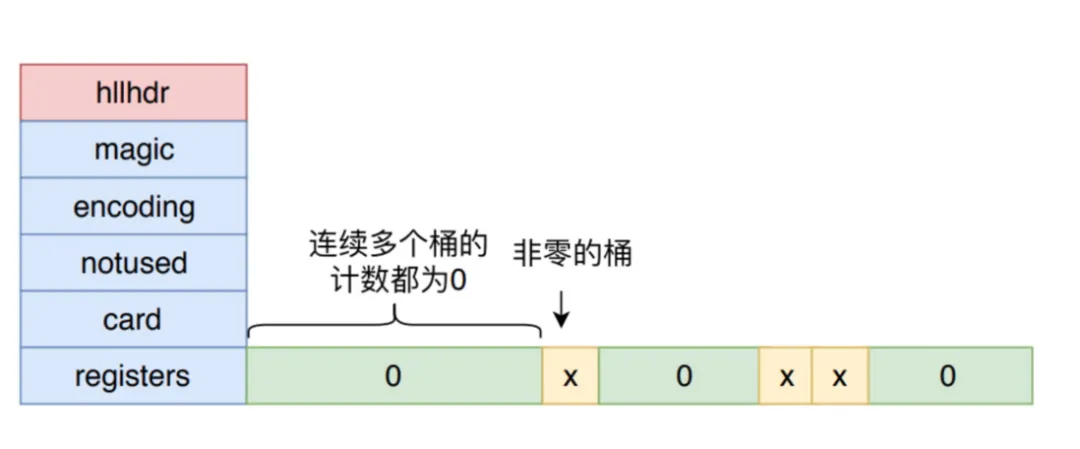
Redis 为了方便表达稀疏存储,它将上面三种 压缩字节结构 表示形式分别赋予了一条指令。
- 压缩结构 ZERO : 一字节,8位,00打头,表示连续多少个桶计数为0,前两位为标志00,后6位表示有多少个桶,最大为64。
- 压缩结构 XZERO : 两个字节,16位,01打头,表示连续多少个桶计数为0,前两位为标志01,后14位表示有多少个桶,最大为16384。
- 压缩结构 VAL : 一字节,8位,1打头,表示连续多少个桶的计数为多少,前一位为标志1,四位表示连桶内计数,所以最大表示桶的计数为32。后两位表示连续多少个桶。
ZERO 压缩结构,一个字节 , 示意图如下:
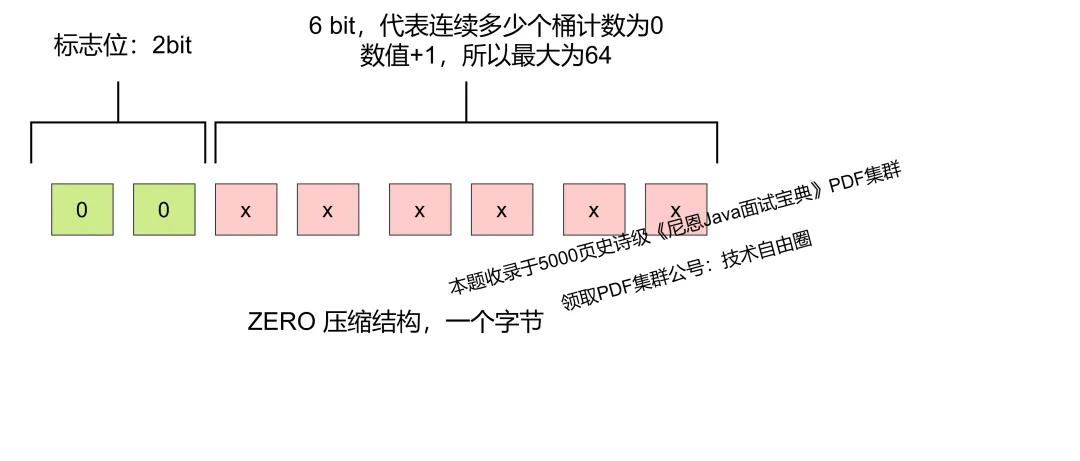
一个 ZERO 压缩结构,最大可以表示 64个 挨着的 0, 也就是如果 64个 空桶挨着,用一个字节就可以,不用 64个字节(准确来说是 64个6位桶), 一下就压缩了 64倍。
压缩结构 XZERO 两个字节,16位 , 示意图如下:
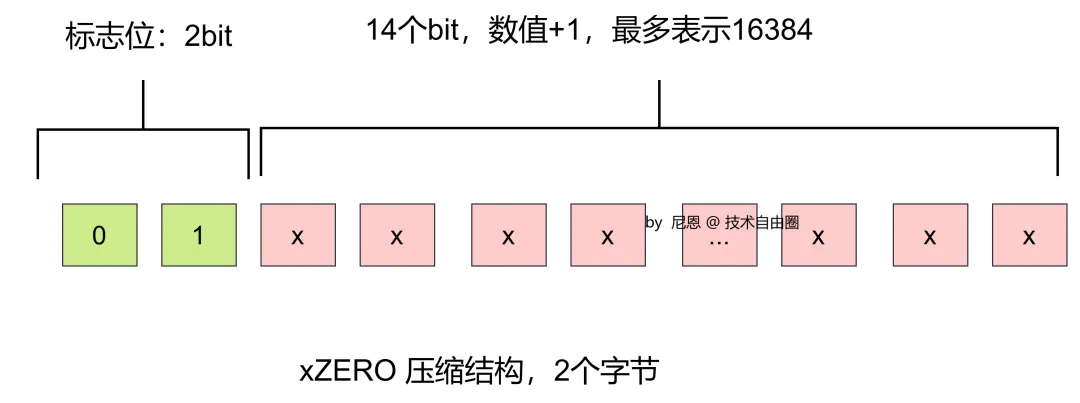
一个x ZERO 压缩结构,最大可以表示 16384个 挨着的 0, 也就是如果 16384个 空桶挨着,用一个字节就可以,不用 16384个字节(准确来说是 16384个6位桶), 一下就压缩了 16384倍,这个是大概哈。
所以,一个初始状态的 HyperLogLog 对象只需要2 字节,也就是一个 XZERO 来存储其数据,而不需要消耗12K 内存。

当 HyperLogLog 插入了少数元素时,可以只使用少量的 XZERO、VAL 和 ZERO 进行表示,如下图所示。
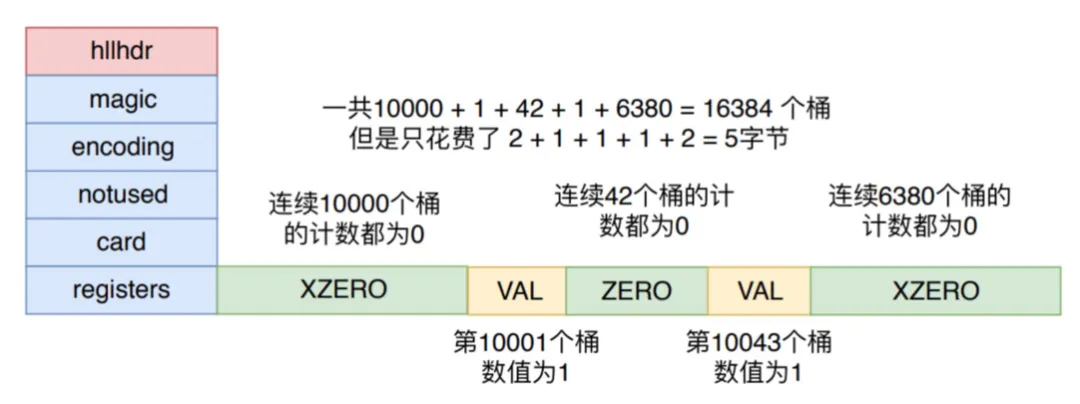
稀疏存储 转换到密集存储的条件是:
- 任意一个计数值从 32 变成 33,因为 VAL 指令已经无法容纳,它能表示的计数值最大为 32
- 稀疏存储占用的总字节数超过 3000 字节,这个阈值可以通过 hll_sparse_max_bytes 参数进行调整。
在线动态观察HyperLogLog算法
首先来一个非常实用的网站,可以在线动态观察HyperLogLog算法。
http://content.research.neustar.biz/blog/hll.html
需要注意的是,此网站 value hash后的值是24位,不是HyperLogLog MurmurHash64A()后的64位,不过也不影响观察学习其原理了。
尼恩架构团队塔尖的redis 面试题
京东面试:亿级 数据查重,亿级 数据黑名单 ,如何实现?(此文介绍了布隆过滤器、布谷鸟过滤器)
史上最全: Redis: 缓存击穿、缓存穿透、缓存雪崩 ,如何彻底解决?
史上最全: Redis锁如何续期 ?Redis锁超时,任务没完怎么办?
技术自由的实现路径:
实现你的 架构自由:
《阿里二面:千万级、亿级数据,如何性能优化? 教科书级 答案来了》
《峰值21WQps、亿级DAU,小游戏《羊了个羊》是怎么架构的?》
… 更多架构文章,正在添加中
实现你的 响应式 自由:
这是老版本 《Flux、Mono、Reactor 实战(史上最全)》
实现你的 spring cloud 自由:
《Spring cloud Alibaba 学习圣经》 PDF
《分库分表 Sharding-JDBC 底层原理、核心实战(史上最全)》
《一文搞定:SpringBoot、SLF4j、Log4j、Logback、Netty之间混乱关系(史上最全)》
实现你的 linux 自由:
实现你的 网络 自由:
《网络三张表:ARP表, MAC表, 路由表,实现你的网络自由!!》
实现你的 分布式锁 自由:
实现你的 王者组件 自由:
《队列之王: Disruptor 原理、架构、源码 一文穿透》
《缓存之王:Caffeine 源码、架构、原理(史上最全,10W字 超级长文)》
《Java Agent 探针、字节码增强 ByteBuddy(史上最全)》
实现你的 面试题 自由:
免费获取11个技术圣经PDF:



