计算机组成原理之计算
有符号数与无符号数
+表示正数，-表示负数
原码表示法
-
使用0表示正数、1表示负数
-
规定符号位位于数值第一位
-
表达简单明了，是人类最容易理解的表示法
二进制的补码表示法
例子1：n=4，x=13，计算x的二进制原码和补码
例子2：x=-13，计算x的二进制原码和补码
例子3：x=-7，计算x的二进制原码和补码
例子4：x=-1，计算x的二进制原码和补码
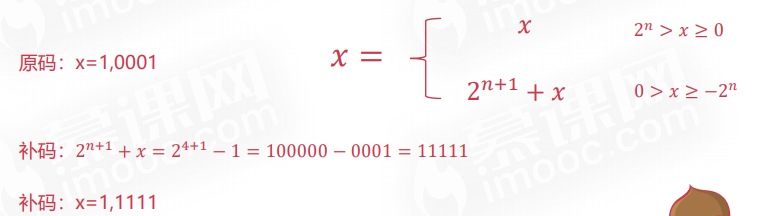
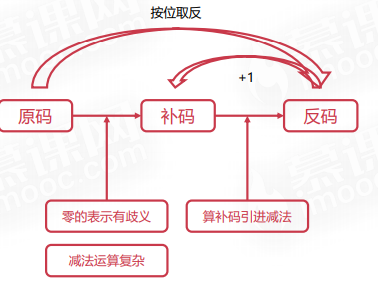
二进制的反码表示法
引进补码的目的（在计算补码的过程中，还是使用了减法！！）
-
减法运算复杂，希望找到使用正数替代负数的方法
-
使用加法代替减法操作，从而消除减法
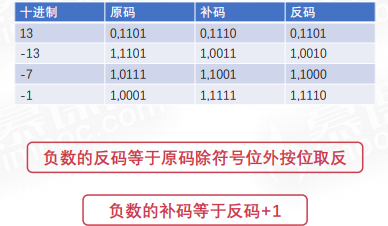
例子1：x=-13，计算x的二进制原码和反码
例子2：x=-7，计算x的二进制原码和反码
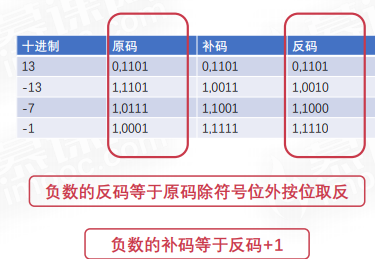
例子3：x=-7，计算x的二进制原码和反码和补码
小数的补码
定点数与浮点数
定点数的表示方法
小数点固定在某个位置的数称之为定点数
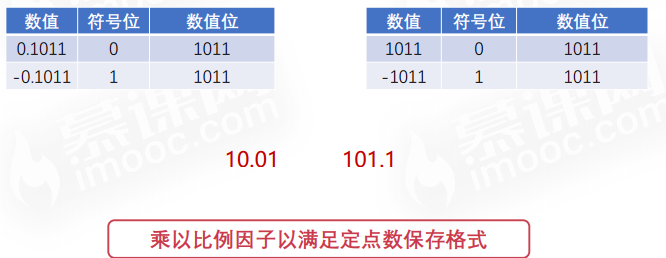
浮点数的表示方法
-
计算机处理的很大程度上不是纯小数或纯整数
-
数据范围很大，定点数难以表达
浮点数的表示格式
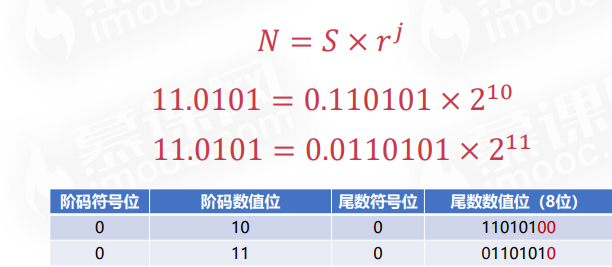
浮点数的表示范围
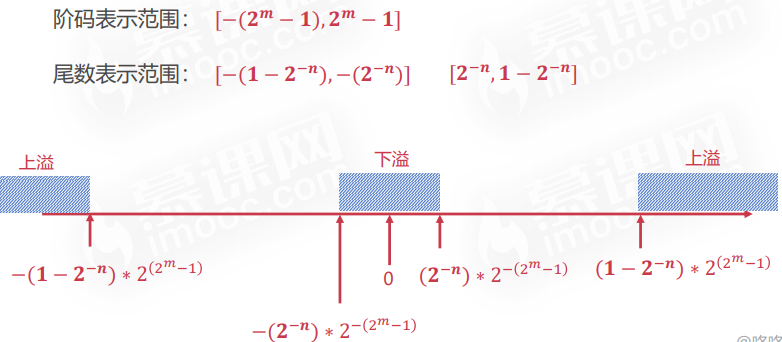
单精度浮点数： 使用4字节、32位来表达浮点数(float)
双精度浮点数： 使用8字节、64位来表达浮点数(double)
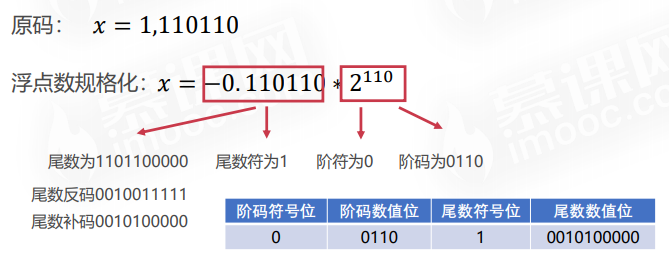
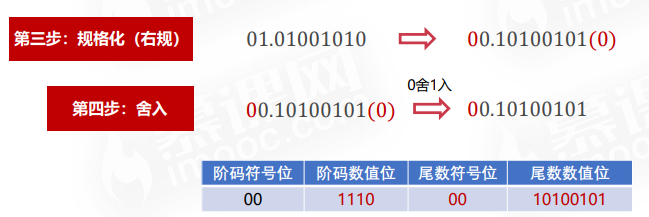
浮点数的规格化
例子1：设浮点数字长为16位，阶码为5位，尾数为11位，将十进制数 13 128表示 为二进制浮点数。
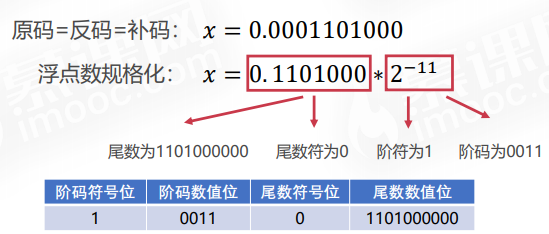
例子2：设浮点数字长为16位，阶码为5位，尾数为11位，将十进制数−54表 示为二进制浮点数。
定点数与浮点数的对比
-
当定点数与浮点数位数相同时，浮点数表示的范围更大
-
当浮点数尾数为规格化数时，浮点数的精度更高
-
浮点数运算包含阶码和尾数，浮点数的运算更为复杂
定点数的加减法运算
例子1：A=-110010， B=001101，求A+B
例子2：A=-0.1010010， B=0.0110100，求A+B
例子3：A=-10010000， B=-01010000，求A+B
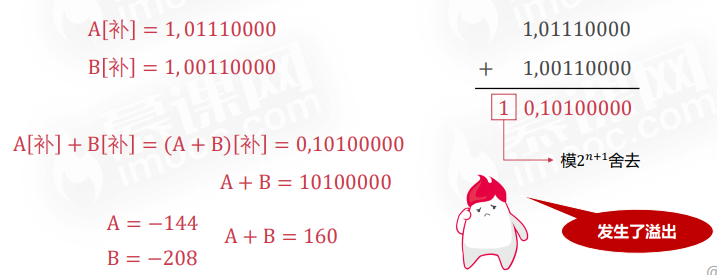
例子4：A=-10010000， B=-11010000，求A+B
判断溢出
例子4：A=-10010000， B=-11010000，求A+B
例子3：A=-10010000， B=-01010000，求A+B
例子5：A=11001000， B=-00110100，求A-B
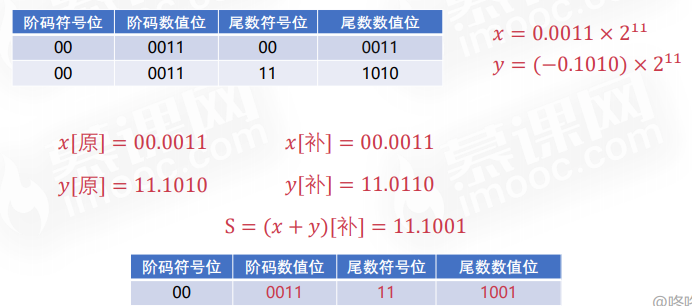
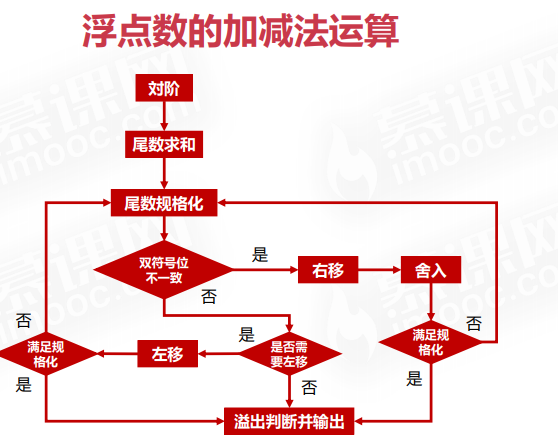
浮点数的加减法运算
尾数求和
-
使用补码进行运算
-
减法运算转化为加法运算：A - B = A + (-B)
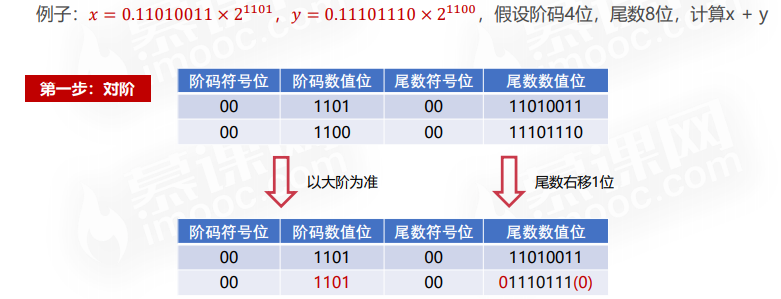
浮点数的乘除法运算
