最小生成树（Kruskal）
题目描述
如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz
输入输出格式
输入格式：
第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）
接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式：
输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz
输入输出样例
说明
时空限制：1000ms,128M
数据规模：
对于20%的数据：N<=5，M<=20
对于40%的数据：N<=50，M<=2500
对于70%的数据：N<=500，M<=10000
对于100%的数据：N<=5000，M<=200000
样例解释：
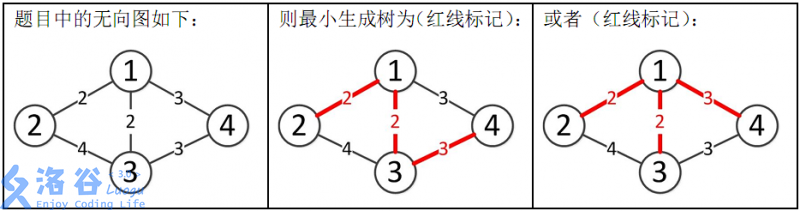
所以最小生成树的总边权为2+2+3=7
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。--分割线
Kruskal其实是一个贪心算法（较容易理解）O(∩_∩)O~~
区别一下prim：
Prim在稠密图中比Kruskal优，在稀疏图中比Kruskal劣。Prim是以更新过的节点的连边找最小值，Kruskal是直接将边排序。
当然我们知道Kruskal是个容易理解的方法
所以这里仅仅讲一下Kruskal（蒟蒻只能讲Kruskal）
------------------------------------------------------------------------------------以下是个人见解（可能是片面的）
我们要找一个加权最小的树
所以我们要边们尽可能的小
所以贪心算法的本质就显现出来了
我们只要先排序，以从小到大的顺序开始加权
当我们发现一条边的两端两个点已经被连起时
这条线其实就是无用的是浪费
所以跳过ta继续
下面是 Taday_Bule_RainbowDALAO的图：
那么我们应该如何搜索是否链接呢？
并查集就可以解决了！
如果两点具有相同祖先那么就是已经连接的点了！
具体见代码哦。
不懂并查集的小伙伴戳这里：https://www.cnblogs.com/crazily/p/10121934.html
还有最后一个问题未解决：end
我们知道一个最小生成树若有n个点那么他就会有n-1条边
所以当我们搜齐n-1条边后就建树完毕了
上代码：
#include<bits/stdc++.h> using namespace std; long long ans; int n,m; int f[200005]; int find(int k){ if(f[k]==k){ return k; } return f[k]=find(f[k]); } struct node{ int x,y; int z;//sum }tree[200005]; bool cmpp(node x,node y){ return x.z<y.z; } void Kruskal(int i,int a){ if(a==n-1){ return; } if(find(tree[i].x)==find(tree[i].y)){ Kruskal(i+1,a); return; } ans+=tree[i].z; f[find(tree[i].x)]=f[tree[i].y]; Kruskal(i+1,a+1); } int main(){ cin>>n>>m; if(n>m) {cout<<"orz"<<endl;return 0;} for(int i=1;i<=m;++i){ scanf("%d%d%d",&tree[i].x,&tree[i].y,&tree[i].z); } sort(tree+1,tree+1+m,cmpp); for(int i=1;i<=m;++i){ f[i]=i; } Kruskal(1,0); cout<<ans<<endl; } /* 样例输入： 5 18 2 4 276 3 3 435 3 4 608 2 4 860 1 2 318 1 3 547 5 4 419 2 5 98 1 5 460 5 3 399 3 5 240 3 2 733 3 3 903 4 2 909 5 2 206 3 4 810 2 1 115 2 3 419 样例输出： 729 */
//（悄咪咪）其实题目里那个orz情况在评分数据里并没有。。。。。
