堆模板（STL版）

题目描述

如题，初始小根堆为空，我们需要支持以下3种操作：

操作1： 1 x 表示将x插入到堆中

操作2： 2 输出该小根堆内的最小数

操作3： 3 删除该小根堆内的最小数

输入输出格式

输入格式：

 

第一行包含一个整数N，表示操作的个数

接下来N行，每行包含1个或2个正整数，表示三种操作，格式如下：

操作1： 1 x

操作2： 2

操作3： 3

 

输出格式：

 

包含若干行正整数，每行依次对应一个操作2的结果。

 

输入输出样例

输入样例#1： 复制

5
1 2
1 5
2
3
2

输出样例#1： 复制

2
5

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=15

对于70%的数据：N<=10000

对于100%的数据：N<=1000000（注意是6个0。。。不过不要害怕，经过编者实测，堆是可以AC的）

样例说明：

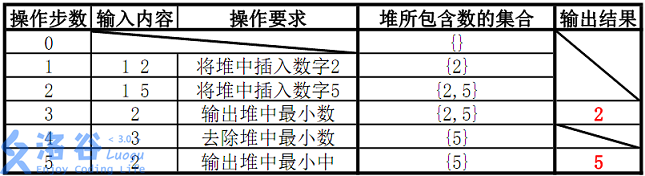
故输出为2、5

。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。--分割线

堆，这是个比较令人熟悉的容器

ta无非是维持一棵具有单调性的树（从小到大 OR 从大到小）

所以它可以将一次搜索的时杂变成O（log n）；

具体看代码吧

这里是stl的版本：（其实那后面那个手写版本是有问题的，可我太弱，目前还没调出来）

#include<bits/stdc++.h>
using namespace std;

//priority_queue<int> q 大根堆 
priority_queue<int, vector<int>, greater<int> > q;//小根堆 (<int>后要加‘ ’)
/*
q.top()//取得堆顶元素，并不会弹出
q.pop()//弹出堆顶元素
q.push()//往堆里面插入一个元素
q.empty()//查询堆是否为空，为空则返回1否则返回0
q.size()//查询堆内元素数量
*/ 
int main(){
    int n,x;
    cin>>n;
    while(n--){
        int t;
        scanf("%d",&t);
        if(t==1){
            scanf("%d",&x);
            q.push(x);
        }
        if(t==2){
            printf("%d\n",q.top());
        }
        if(t==3){
            q.pop();
        }
    }
} 
/*情怀手写版 
int l;//大小 
int dui[1000005];
void up_dui(int i,bool z){
    if(i==1||z==0){return;}
    if(dui[i/2]>dui[i]) {
        swap(dui[i/2],dui[i]);
    }
    else {
        z=0;
    }
    up_dui(i/2,z);
}
void down_dui(int i){
    if(i>=l) return;
    if(dui[i*2]<dui[i]){
        swap(dui[i*2],dui[i]);
        down_dui(i*2);
        return;
    }
    if(dui[i*2+1]<dui[i]){
        swap(dui[i*2+1],dui[i]);
        down_dui(i*2+1);
        return;
    }
}
void pushn(){
    int x;
    scanf("%d",&x);
    ++l;
    dui[l]=x;
    up_dui(l,1);
}
void popn(){
    printf("%d\n",dui[1]);
}
void deleten(){
    dui[1]=dui[l];
    dui[l]=0;
    --l;
    down_dui(1);
}
int main(){
    cin>>n;
    while(n--){
        int t;
        scanf("%d",&t);
        if(t==1){
            pushn();
        }
        if(t==2){
            popn();
        }
        if(t==3){
            deleten();
        }
    }
} 

*/

//跪求路过DALAO指导（QAQ）