排序算法

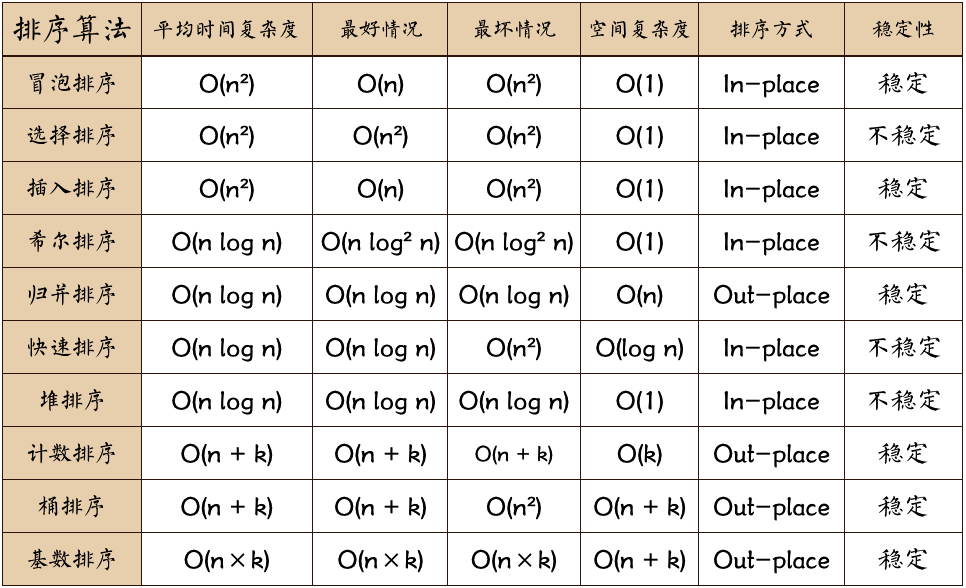
复杂度

• ref: https://segmentfault.com/a/1190000021638663

代码实现

0. 冒泡排序

• 遍历数组, 交换相邻两个元素, 每趟遍历可将一个最大值沉底

void sort(vector<int>& nums) {
    int n = nums.size();
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - 1 - i; j++) {
            if (nums[j] > nums[j+1]) {
                swap(nums[j], nums[j+1]);
            }
        }
    }
}

1. 选择排序

• 在未排序序列中找到最小元素，放到该序列开始位置

void sort(vector<int>& nums) {
    int n = nums.size();
    int min_pos;
    for (int i = 0; i < n - 1; i++) {
        min_pos = i;
        for (int j = i + 1; j < n; j++) {
            if (nums[j] < nums[min_pos]) {
                min_pos = j;
            }
        }
        if (min_pos != i) {
            swap(nums[i], nums[min_pos]);
        }
    }
}

2. 插入排序

void sort(vector<int>& nums) {
    int n = nums.size();
    for (int i = 1; i < n; i++) {
        int cur_num = nums[i];
        int ins_pos;
        for (ins_pos = i; ins_pos >= 1 && nums[ins_pos-1] > cur_num; ins_pos -= 1) {
            nums[ins_pos] = nums[ins_pos-1];
        }
        nums[ins_pos] = cur_num;
    }
}

3. 希尔排序

• 按照一定的步长, 多次执行插入排序
• 可看作是对插入排序的改进

void sort(vector<int>& nums) {
    int n = nums.size();
    for (int gap = n / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < n; i++) {
            int cur_num = nums[i];
            int ins_pos;
            for (ins_pos = i; ins_pos >= gap && nums[ins_pos-gap] > cur_num; ins_pos -= gap) {
                nums[ins_pos] = nums[ins_pos-gap];
            }
            nums[ins_pos] = cur_num;
        }
    }
}

4. 归并排序

• 分治, 合并两个有序数列

void sort(vector<int>& nums) {
    merge_sort(nums, 0, nums.size());
}

• 递归形式归并排序

void merge_sort(vector<int>& nums, int s, int t) {
    if (t - s <= 1) return;

    int m = s + (t - s) / 2;
    merge_sort(nums, s, m);
    merge_sort(nums, m, t);

    merge(nums, s, m, t);
}

• 合并有序数组

void merge(vector<int>& nums, int s, int m, int t) {
    vector<int> l_nums(nums.begin() + s, nums.begin() + m);
    vector<int> r_nums(nums.begin() + m, nums.begin() + t);

    int p = 0, q = 0, k = s;
    int l_n = l_nums.size(), r_n = r_nums.size();

    while (p < l_n && q < r_n) {
        if (l_nums[p] < r_nums[q]) nums[k++] = l_nums[p++];
        else nums[k++] = r_nums[q++];
    }
    while (p < l_n) nums[k++] = l_nums[p++];
    while (q < r_n) nums[k++] = r_nums[q++];
}

5. 快速排序

• 找到 pivot, 时间复杂度 \(O(n)\) 实现左边都比它小, 右边都比它大

void sort(vector<int>& nums) {
    quick_sort(nums, 0, nums.size());
}

• quicksort 主过程

void quick_sort(vector<int>& nums, int s, int t) {
    if (t - s <= 1) return;
    int pivot = partition(nums, s, t);
    quick_sort(nums, s, pivot);
    quick_sort(nums, pivot + 1, t);
}

• partition 过程

int partition(vector<int>& nums, int s, int t) {
    int p = s, q = t - 1;
    int pivot = nums[p];
    while (p < q) {
        while (p < q && nums[q] >= pivot) q--;
        nums[p] = nums[q];
        while (p < q && nums[p] <= pivot) p++;
        nums[q] = nums[p];
    }
    nums[p] = pivot;
    return p;
}

• 注意 “等于” 的情况

6. 堆排序

• 近似完全二叉树 (可以利用数组来表示, 同时有索引映射关系)
• 可看作是对选择排序的改进
• 取出堆顶, 调整为最大堆/最小堆
• ref: https://zhuanlan.zhihu.com/p/45725214

void sort(vector<int>& nums) {
    int n = nums.size();

    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(nums, n, i);
    }

    for (int i = n - 1; i >= 1; i--) {
        swap(nums[0], nums[i]);
        heapify(nums, i, 0);
    }
}

• 将区间范围内调整为大顶堆

void heapify(vector<int>& nums, int n, int cur_root) {
    int pos_max = cur_root;
    int v_left_ = pos_max * 2 + 1;
    int v_right = pos_max * 2 + 2;

    if (v_left_ < n && nums[v_left_] > nums[pos_max]) {
        pos_max = v_left_;
    }
    if (v_right < n && nums[v_right] > nums[pos_max]) {
        pos_max = v_right;
    }

    if (pos_max != cur_root) {
        swap(nums[cur_root], nums[pos_max]);
        heapify(nums, n, pos_max);
    }
}

7. 计数排序

• 不是 “比较” 排序, 需要限定输入数据的范围
• 累计技术, 根据值索引 index

void sort(vector<int>& nums) {
    int n = nums.size();

    int max_v = nums[0];
    for (int i = 1; i < n; i++) {
        if (nums[i] > max_v) {
            max_v = nums[i];
        }
    }

    vector<int> count_nums(max_v + 1, 0);
    for (int i = 0; i < n; i++) {
        count_nums[nums[i]]++;
    }
    for (int i = 1; i <= max_v; i++) {
        count_nums[i] += count_nums[i-1];
    }

    vector<int> temp(nums);
    for (int i = 0; i < n; i++) {
        int cur = temp[i];
        int idx = count_nums[cur] - 1;
        nums[idx] = cur;
        count_nums[cur]--;
    }
}

8. 桶排序

• 计数排序的升级版
• 分为 scatter (映射函数) 和 gather (顺序连接) 两个过程
• 创建桶, 插入桶, 桶内排序, 桶连接

void sort(vector<int>& nums) {
    int n = nums.size();

    int max_v = nums[0];
    for (int i = 0; i < n; i++) {
        if (nums[i] > max_v) {
            max_v = nums[i];
        }
    }
    int bucket_nums = max_v / 100 + 1;
    vector<vector<int>> buckets(bucket_nums, vector<int>());

    for (int i = 0; i < n; i++) {
        int idx = nums[i] / 100;
        buckets[idx].push_back(nums[i]);
    }

    for (int i = 0; i < bucket_nums; i++) {
        sort(buckets[i].begin(), buckets[i].end());
    }

    int cnt = 0;
    for (int i = 0; i < bucket_nums; i++) {
        for (int k = 0; k < buckets[i].size(); k++) {
            nums[cnt++] = buckets[i][k];
        }
    }
}

9. 基数排序

• 桶, 实际上是一种映射函数, 三种排序方法使用的映射方式不同
  • 计数排序: 每个桶只存储单一键值
  • 桶排序: 每个桶存储一定范围的数值
  • 基数排序: 根据键值的每位数字来分配桶
• 基数排序对每 “位” 进行排序
  • 使用 queue, 可以方便桶的合并过程

void sort(vector<int>& nums) {
    int n = nums.size();

    int max_v = nums[0];
    for (int i = 0; i < n; i++) {
        if (max_v < nums[i]) {
            max_v = nums[i];
        }
    }

    vector<queue<int>> buckets(10, queue<int>());

    int max_bits = 1;
    for (int i = max_v / 10; i; i /= 10, max_bits++);

    for (int bit_pos = 1, div_val = 1; bit_pos <= max_bits; bit_pos++, div_val *= 10) {
        for (int i = 0; i < n; i++) {
            int idx = (nums[i] / div_val) % 10;
            buckets[idx].push(nums[i]);
        }

        int cnt = 0;
        for (int i = 0; i < buckets.size(); i++) {
            while (!buckets[i].empty()) {
                nums[cnt++] = buckets[i].back();
                buckets[i].pop();
            }
        }
    }
}

References

• Sorting and Searching https://www.programiz.com/dsa
• 经典排序算法 https://www.runoob.com/w3cnote/ten-sorting-algorithm.html