「POI2013」Multidrink
题目
点这里看题目。
给定一棵包含 \(n\) 个结点的树。
构造一个 \(1\sim n\) 的排列 \(p_1,p_2,\dots,p_n\),满足:
-
\(p_1=1,p_n=n\)。
-
对于任意的 \(1\le k<n\),\(p_k\) 和 \(p_{k+1}\) 之间的距离不超过 \(2\)。
如果不存在,输出 BRAK。如果存在,输出任意一组解。
所有数据满足 \(2\le n\le 5\times 10^5\)。
分析
算是比较友好的构造题了。
首先可以手玩一下“树形为链,且 \(1\) 为一端”——过程和结果都比较简单。从 \(1\) 一路走到 \(n\) 的父亲,之后的交错跳即可。
可以感知到,“距离”限制还是比较紧的。拿这样的经验,分析一下一般树上的起手策略。设 \(v\) 为 \(n\) 所在子树,那么:
-
如果 \(v\) 是唯一的儿子,那么可以直接跳到 \(v\) 子树。
-
如果除了 \(v\) 以外其它儿子都是叶子,那么可以先跳叶子,最后跳到 \(v\) 结点。
-
否则,可以发现 \(v\) 以外最多只能有一个儿子不是叶子,我们记那个儿子为 \(w\)。可以发现,最终我们必须回到 \(w\),那么这个过程类似于链上行走,于是可以构造:
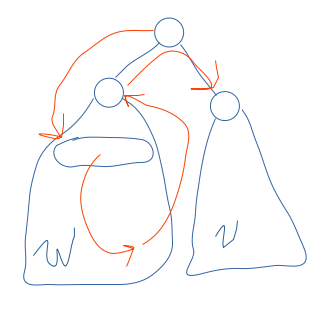
也就是,先跳到 \(w\) 的一个儿子,经过 \(w\) 子树之后到达 \(w\),然后从 \(w\) 跳到 \(v\) 结点。
这些考虑起来都比较简单,但一定要分清楚:情况 1 和情况 2,3 是本质不同的。前者是从 \(v\) 的父亲出发(第一类),而后者是从 \(v\) 出发(第二类)。第二类可以遍历完的情况时第一类的真子集。从 \(1\) 出发就属于第二类,因此我们已经分析完了第二类的走法了。
在此之前,我们先来解决 \(w\) 的问题(第三类)。考虑一个类似于第二类的情况:我们需要从 \(s\) 出发,遍历完 \(s\) 子树后回到 \(s\) 的一个儿子上。那么:
-
如果 \(s\) 的所有儿子都是叶子,略。
-
如果 \(s\) 有儿子不是叶子,则这样的儿子至多只有一个,有多个就无法回到 \(s\) 的儿子之中了。
设非叶子儿子为 \(w\),构造策略基本同第二类 3.:先走到 \(w\) 的一个儿子,遍历完之后回到 \(w\),然后从 \(w\) 开始遍历完所有叶子。
为了 2. 我们需要再构造一个“第四类”问题吗?显然过于复杂。我们注意到路径具有天然的对称性。也就是说,如果我们将第三类输出的路径反过来,恰好就是“从 \(s\) 的一个儿子出发,遍历完子树后回到 \(s\) 的路径”!只需要快速地处理“反序”即可,后面再来讨论。
相应地,第二类 3. 也可以直接用第三类问题的解法解决,于是我们额外讨论一下第一类。
贪心地想,从 \(s\) 出发,如果 \(n\) 在 \(v\) 的子树内,我们就应该尽量让 \(v\) 也可以面对“第一类”的情况。此外,结合样例我们可以得到一点提示。设 \(c\) 为“非叶子儿子或包含 \(n\) 的儿子总个数”,则有:
-
如果 \(c=1\),则先遍历叶子儿子,而后经过 \(s\),最后进入 \(v\) 的子树,变成第一类子问题。
-
如果 \(c=2\),设另外的非叶子儿子为 \(w\),则:
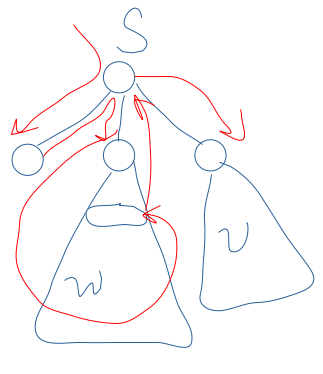
应当先遍历叶子,再到达 \(w\),遍历完其子树后到达 \(w\) 的一个儿子,而后到达 \(s\),最后进入 \(v\) 的子树,变成第一类子问题。
-
如果 \(c=3\),设另外两个非叶子儿子为 \(w,x\),则:
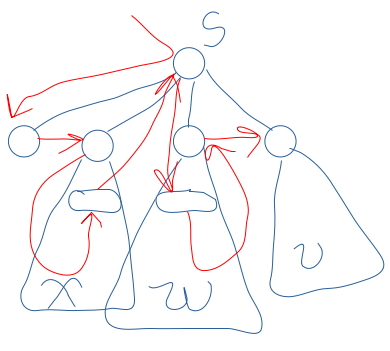
应当先遍历叶子,再到达 \(x\),遍历完其子树后到达 \(x\) 的一个儿子,而后到达 \(s\),再到达 \(w\) 的一个儿子,遍历完 \(w\) 后到达 \(w\),最后到达 \(v\) 结点,变成第二类子问题。
最后需要处理一下“倒序”的问题。
在代码实现中,事实上将“倒序”单独写成一个函数可以得到更简单的逻辑。不过,由于子树大小确定,所以我们可以提前知道某个子树最终会占据的区间。而方向也可以在进入子树前得知,因此另一种方法就是改变填写位置和方向模拟倒序。两种都可以线性处理。
最终我们可以 \(O(n)\) 得到结果。
代码
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <algorithm>
#define rep( i, a, b ) for( int i = (a) ; i <= (b) ; i ++ )
#define per( i, a, b ) for( int i = (a) ; i >= (b) ; i -- )
const int MAXN = 5e5 + 5;
template<typename _T>
inline void Read( _T &x ) {
x = 0; char s = getchar(); bool f = false;
while( s < '0' || '9' < s ) { f = s == '-', s = getchar(); }
while( '0' <= s && s <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar(); }
if( f ) x = -x;
}
template<typename _T>
inline void Write( _T x ) {
if( x < 0 ) putchar( '-' ), x = -x;
if( 9 < x ) Write( x / 10 );
putchar( x % 10 + '0' );
}
struct Edge {
int to, nxt;
} Graph[MAXN << 1];
std :: vector<int> son[MAXN];
int ans[MAXN], tot;
int siz[MAXN]; bool imp[MAXN];
int head[MAXN], cnt = 1;
int N;
#define Dead {\
puts( "BRAK" );\
exit( 0 );\
}
inline void AddEdge( const int &from, const int &to ) {
Graph[++ cnt].to = to, Graph[cnt].nxt = head[from];
head[from] = cnt;
}
void Init( const int &u, const int &fa ) {
siz[u] = 1, imp[u] = u == N;
for( int i = head[u], v ; i ; i = Graph[i].nxt )
if( ( v = Graph[i].to ) ^ fa ) {
Init( v, u );
siz[u] += siz[v];
imp[u] |= imp[v];
son[u].push_back( v );
}
std :: sort( son[u].begin(), son[u].end(),
[] ( const int &a, const int &b ) -> bool {
if( imp[b] ) return true;
if( imp[a] ) return false;
return siz[a] < siz[b];
} );
}
void DFS2( const int &u, const int &fa, int cur, const int &dir ) {
// 根本不需要关心到 u 的距离!
// 如果最开始就是从 u 出发的,那么最后必须到 u 的一个儿子
// 把整个路径反过来就可以得到从一个儿子出发的路径!
ans[cur += dir] = u;
int n = son[u].size(), sml = 0, lrg;
rep( i, 0, n - 1 )
sml += siz[son[u][i]] == 1;
lrg = n - sml;
if( lrg >= 2 ) Dead
if( lrg ) {
DFS2( son[u][n - 1], u, cur + dir * ( siz[son[u][n - 1]] + 1 ), - dir );
cur += dir * siz[son[u][n - 1]];
}
rep( i, 0, sml - 1 ) ans[cur += dir] = son[u][i];
}
void DFS1( const int &u, const int &fa, const int &d, int cur, const int dir ) {
// d = 0: 从 u 出发
// d = 1: 从 u 的父亲出发
// 注意这里的目标是到达 N,而不是回到 u 附近,所以需要记录 d
int n = son[u].size(), sml = 0, lrg;
rep( i, 0, n - 1 )
sml += siz[son[u][i]] == 1 && ! imp[son[u][i]];
lrg = n - sml;
if( u == N ) {
if( d == 0 && siz[u] > 1 ) Dead
DFS2( u, fa, cur + dir * ( siz[u] + 1 ), - dir );
} else if( d == 1 ) {
if( lrg > 3 ) Dead
rep( i, 0, sml - 1 )
ans[cur += dir] = son[u][i];
if( lrg == 3 ) {
DFS2( son[u][n - 3], u, cur, dir );
cur += dir * siz[son[u][n - 3]], ans[cur += dir] = u;
DFS2( son[u][n - 2], u, cur + dir * ( siz[son[u][n - 2]] + 1 ), - dir );
cur += dir * siz[son[u][n - 2]];
DFS1( son[u][n - 1], u, 0, cur, dir );
} else {
if( lrg == 2 ) {
DFS2( son[u][n - 2], u, cur, dir );
cur += dir * siz[son[u][n - 2]];
}
ans[cur += dir] = u;
DFS1( son[u][n - 1], u, 1, cur, dir );
}
} else {
if( lrg > 2 ) Dead
ans[cur += dir] = u;
if( lrg == 2 ) {
DFS2( son[u][n - 2], u, cur + dir * ( siz[son[u][n - 2]] + 1 ), - dir );
cur += dir * siz[son[u][n - 2]];
}
rep( i, 0, sml - 1 ) ans[cur += dir] = son[u][i];
DFS1( son[u][n - 1], u, n == 1, cur, dir );
}
}
int main() {
Read( N );
rep( i, 1, N - 1 ) {
int u, v; Read( u ), Read( v );
AddEdge( u, v ), AddEdge( v, u );
}
Init( 1, 0 );
DFS1( 1, 0, 0, 0, 1 );
rep( i, 1, N )
Write( ans[i] ), putchar( '\n' );
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号