数学杂谈 #14

Period and Border

简明的定义

• 字符集：表示字符串中所有可能出现的字符的集合，通常用 \(\Sigma\) 表示。

  一般来说，我们遇到的字符集为小写字符集 \(\Sigma=\{'a','b','c',\dots,'z'\}\)。

• 字符串：字符串的集合可以用如下定义：

  \[S=\bigcup_{k\ge 0}\Sigma^k \]

  这个集合中的元素的直观理解就是我们通常所知的字符串——由若干个（可以为零个）字符集内的字符顺序构成的......一串东西。

  通常我们习惯用 \(s\) 表示在当前字符集下的一个字符串。

• 字符串的长度：对于字符串 \(s\)，我们通常就用 \(|s|\) 表示它的长度，也就是所含字符个数。

• 字符串的拼接：对于字符串 \(u,v\)，我们可以用 \(uv\) 表示将 \(v\) 的字符按照顺序添加入 \(u\) 的末尾后得到的字符串。

• 子串：对于字符串 \(s\)，我们习惯于对于它的字符写成一行，然后从左往右按顺序编号为 \(1,2,\dots,|s|\)。

  如是我们可以用 \(s[k]\) 表示编号为 \(k\) 的字符。

  接着我们可以定义子串，用 \(s[l:r]\) 表示 \(s[l]s[l+1]\dots s[r]\) 拼接而成的字符串，且需要满足 \(1\le l\le r\le |s|\)。特别地，在某些情况下，我们会认为 \(l>r\) 代表了 \(s[l:r]\) 为空串，即不包含任何字符的字符串。

  较为特殊的子串是前缀和后缀。我们会用 \(\newcommand{\Pre}{\operatorname{Pre}}\Pre(s,l)\) 表示 \(s[1:l]\)，用 \(\newcommand{\Suf}{\operatorname{Suf}}\Suf(s,l)\) 表示 \(s[|s|-l+1:|s|]\)。自然需要满足 \(1\le l\le |s|\)，但当 \(l=0\) 的时候，我们一般会认为 \(\newcommand{\Pre}{\operatorname{Pre}}\Pre(s,0)\) 和 \(\newcommand{\Suf}{\operatorname{Suf}}\Suf(s,0)\) 返回空串。

• 字符串的幂：如果我们将字符串的拼接看作是“乘法”操作，那么相应地，我们可以定义“幂”：用 \(s^p\) 表示 \(p\) 个 \(s\) 的拼接结果。

  \(p\in \mathbb N\) 的情况不多说。特别地，\(p\) 可以是一个有理数。不妨设 \(p=\frac{a}{b},\gcd(a,b)=1\)，则 \(s^p\) 表示 \(\newcommand{\Pre}{\operatorname{Pre}}s^{\lfloor\frac{a}{b}\rfloor}\Pre(s,|s|\times \frac{a\bmod b}{b})\)。这个定义带来了限制，也就是 \(b| |s|\)。

• 字符串的比较：对于字符串 \(u,v\)，如果 \(|u|=|v|\) 且 \(\forall 1\le k\le |u|,u[k]=v[k]\)，我们就说 \(u=v\)。

Period

字符串可以看作是数列，数列可以看作是特殊的函数，因此字符串的周期也和函数的周期非常类似。这些东西有必然联系吗？

对于字符串 \(s\)，如果有整数 \(0<T\le |s|\)，且满足 \(\forall1\le k\le |s|-T,s[k]=s[k+T]\)，则称 \(T\) 为 \(s\) 的一个周期。

一般来说，我们主要在讨论最小正周期，因此我们可以用 \(\newcommand{\Per}{\operatorname{Per}}\Per(s)\) 表示字符串 \(s\) 的最小的周期。

一种等价的理解是，如果 \(T\) 是 \(s\) 的周期，那么 \(s\) 就应该是 \(\Pre(s,T)^{\infty}\) 的前缀，或者 \(s=\Pre(s,T)^{\frac{|s|}{T}}\)。

Weak Periodicity Lemma

这个叫做弱周期引理，至于为什么“弱”，待会儿你就知道了。内容如下：

对于一个字符串 \(s\)，如果有 \(p,q\) 都是 \(s\) 的周期，并且 \(p+q\le |s|\)，则可以得出 \(\gcd(p,q)\) 也是 \(|s|\) 的周期。

这个东西挺好理解的，也挺好证明的：

对于 \((p,q)\) 进行归纳证明。

首先，我们不妨假设 \(p\le q\)。边界的情况就是 \(p=1\)，此时 \(\gcd(1,q)=1=p\)，显然成立。

接着，考虑 \(1<p\le q\) 的情况。假设该定理对于任意的 \((x,y)\) 都已被证明，其中 \(x<p\) 或 \(y<q\) 成立。

由于 \(p+q\le |s|\)，则对于 \(1\le k\le |s|\)，有 \(k\le |s|-q\) 或 \(k>p\) 其一成立。

前者可以推出 \(s[k]=s[k+q-p]\)，而后者可以推出 \(s[k]=s[k-p+q]\)。总而言之，我们得到了 \(q-p\) 也是 \(s\) 的一个周期。

由于 \(q-p<q\)，根据归纳假设可以知道 \(\gcd(p,q-p)\) 也是 \(s\) 的一个周期，所以 \(\gcd(p,q)\) 也是 \(s\) 的一个周期。

说白了，不就是辗转相除的过程吗。

Periodicity Lemma

这就是正版的周期引理。至于为什么不“弱”，你待会儿就知道了。内容如下：

对于一个字符串 \(s\)，如果有 \(p,q\) 都是 \(s\) 的周期，并且 \(p+q\le |s|+\gcd(p,q)\)，则可以得出 \(\gcd(p,q)\) 也是 \(s\) 的周期。

证明看起来非常复杂，这里就感性理解一下吧。

Border

直译过来应该叫做字符串的“边界”，不过我着实没有看见过任何一个人这样称呼它的。

不过，从词语的含义入手，这个定义其实还是相当易于理解的：

对于一个字符串 \(s\)，如果存在整数 \(0\le r<|s|\)，且满足 \(\Pre(s,r)=\Suf(s,r)\)，那么就称 \(\Pre(s,r)\) 为 \(s\) 的一个 Border。

在下文你有可能看见，我们会用 \(\newcommand{\Bord}{\operatorname{Border}}\Bord(s)\) 表示 \(s\) 的所有 Border 构成的集合。

Border and Period

我们在这里将要讨论 Border 和 Period 的对偶性。说白了就是，周期和 Border 存在一一对应的关系。

• 从周期到 Border 时，我们选一个周期 \(T\)。根据定义，\(\forall 1\le k\le |s|-T,s[k]=s[k+T]\)，换言之就是 \(\Pre(s,|s|-T)=\Suf(s,|s|-T)\)；
• 而从 Border 到周期时，我们选某个 Border \(b\)，且令 \(r=|b|\)，则由 \(\Pre(s,r)=\Suf(s,r)\) 可以得到 \(\forall 1\le k\le r,s[k]=s[k+|s|-r]\)。

这一点很重要，因为我们马上就可以看到它的应用。

Structure of Border

从字符串本身来看，我们不难得出：Border 的 Border 还是 Border。

假设有字符串 \(s\)，且 \(|\Bord(s)|>1\)。

取 \(u\in \Bord(s)\)，再取 \(v\in \Bord(u)\)。

根据定义有 \(v=\Pre(u,|v|)=\Pre(s,|v|)=\Suf(u,|v|)=\Suf(s,|v|)\)，因此 \(v\in \Bord(s)\)。

我决定称上述命题为 BBaB 命题，来源于 Border's Border is still a Border。

一个更加重要的论断是：

取出 \(p=\arg\max\{|b||b\in \Bord(s)\}\)，那么 \(\Bord(s)=\Bord(p)\cup\{p\}\)。

我们平时写 KMP 找 Border，其实就基于上述论断。

如果上述命题为伪，那么我们可以取出 \(x\in \Bord(s)\)，且 \(x\neq p,x\not\in\Bord(p)\)。

由于 \(p\) 的性质，我们可以知道 \(|x|<p\)。类似于 BBaB 的证明方式，我们可以说明 \(x\) 应当 \(\in \Bord(p)\)，矛盾。

这个论断告诉我们，我们可以用树来描述每一个前缀的 \(\Bord()\)，这样每个结点的 \(\Bord()\) 就是树根到该节点的路径上，所有结点对应的字符串的集合。

---

从数值上看，我们先需要两个引理。

引理之一：

对于字符串 \(s\)，它的所有长度 \(\ge \lceil\frac{|s|}2\rceil\) 的 Border 的长度可以构成一个等差数列。

特别提醒：我们这里将 \(s\) 本身也看作是它的一个 Border，也即 Border 的长度取值范围为 \([0,|s|]\)。

证明就需要将 Border 的问题转化到周期上面来：

设 \(p=\Per(s)\)。如果有 \(p>\lfloor\frac{|s|}{2}\rfloor\)，那么就没什么可说的了。

否则，取另外一个周期 \(p<q\le \lfloor\frac{|s|}{2}\rfloor\)。如果不存在这样的 \(q\) ，那也没什么可说的。

否则，根据 Weak Lemma，我们可以知道 \(\gcd(q,p)\) 也是一个周期，结合 \(\gcd\) 的性质我们可以知道 \(p=\gcd(q,p)\)。

因此有 \(p|q\)。由于 \(q\) 的任意性，我们可以知道 \(p,2p,3p,\dots,q\) 都是周期，并且给出的相邻两项之间不存在任何别的周期。

将周期对应到 Border 上，我们就得到了引理。额外的修正来自于 \(s\) 本身，我们只需要将 0 加入到首位即可。

---

接着是引理之二：

对于字符串 \(u,v\)，如果 \(|u|=|v|=n\)，我们则定义 \(\newcommand{\PS}{\operatorname{PS}}\PS(u,v)=\{k|\Pre(u,k)=\Suf(v,k)\}\)。

此外的定义是 \(\newcommand{\LPS}{\operatorname{LargePS}}\LPS(u,v)=\{k|\Pre(u,k)=\Suf(v,k),\lceil\frac{n}{2}\rceil\le k\le n\}\)。

那么有：\(\LPS(u,v)\) 中的元素可以构成一个等差数列。

这个引理其实就是引理之一的推广，因为上面一个引理讨论的就是 \(\LPS(s,s)\) 的情况。

因此，证明可以直接顺着这个思路来：

不妨假设 \(|\LPS(u,v)|>2\)，取出 \(p=\max \LPS(u,v)\)。

此时对于任意的 \(x\in \LPS(u,v)\setminus\{p\}\)，都有 \(\Pre(u,x)\in \Bord(p)\)，这一步仍然无比类似于 BBaB 的论证方式。

因此，我们可以得到 \(\LPS(u,v)=\{|p|\}\cup \{|b||b\in \Bord(p),|b|\ge \lceil\frac n 2\rceil\}\)。由于 \(\lceil\frac p 2\rceil\le \lceil\frac n 2\rceil\)，我们即可结合引理之一得到证明。

---

以下是最终的推论：

对于任何一个字符串 \(s\)，它的所有 Border 可以按照长度被划分为 \(O(\log |s|)\) 个等差数列。

我们先设 \(n=|s|\)。构造方法有两种：

• 递归构造。先取出 \(\LPS(s,s)\)，然后构造出一个等差数列。

  构造结束后剩下长度 \(\le \lfloor\frac n2\rfloor\) 的 Border，直接递归进入 \(\LPS(\Pre(s,\lfloor\frac n 2\rfloor),\Suf(s,\lfloor\frac n 2\rfloor))\) 构造。

  每次长度折半，因此最终会得到 \(O(\log |s|)\) 个等差数列。

• 直接按照长度划分。我们暂时不考虑长度为 0 的 Border。

  这样我们可以将 \([1,n)\) 划分为 \([1,2)\cup[2,4)\cup\dots\cup[2^{k-1},2^k)\cup[2^k,n)\)，其中 \(k\) 是整数且满足 \(2^k\le n<2^{k+1}\)。

  对于其中的一个区间，我们将会说明长度落在该区间内的 Border 可以构成等差数列。

  • 对于区间 \([2^k,n)\)，我们知道 \(2^k\ge \lceil\frac n 2\rceil\)，因此可以构成等差数列。
  • 对于区间 \([2^j,2^{j+1}),0\le j<k\)，我们面对的就是 \(\LPS(\Pre(s,2^{j+1}-1),\Suf(s,2^{j+1}-1))\)，还是可以构成等差数列。

KMP

我们在此定义 \(\newcommand{\nxt}{\operatorname{nxt}}\nxt_k\) 表示 \(\max\{|b||b\in \Bord(\Pre(s,k))\}\)，显然应当满足 \(1\le k\le |s|\)。

KMP 最核心的部分就是求出指定字符串 \(s\) 中每个 \(k\) 的 \(\nxt\)，之后的字符串匹配不过就是一个应用。

这是一个增量的算法，也就是我们可以在 \(s\) 后加入一个字符 \(c\) 而回答 \(s'=sc\) 的 \(\nxt\)。当然，由于 \(\nxt\) 仅仅和前缀相关，我们只需要求出 \(\nxt_{|s'|}\) 就好了。

这个算法的关键就在于，我们要知道 \(\Bord(s')\subseteq \{bc|b\in \Bord(s)\}\)，这个不难理解或证明。因此，在我们求 \(\nxt_{|s'|}\) 的时候，我们只需要按照长度从大到小枚举 \(\Bord(s)\) 中的元素，检查能不能往后塞一个 \(c\)。根据 \(\Bord()\) 的结构，我们可以直接跳 \(\nxt\) 链完成按顺序枚举这个过程。

---

KMP 的复杂度是均摊 \(O(n)\) 的，此处略过。不过，由于 KMP 还是一个增量算法，因此我们可以动态地向字符串后面“插入”字符而保证复杂度正确这不废话么。但是如果存在删去字符的情况，那分析就失效了——也就是 KMP 不能回退。

Period's' of a Substring

这个部分看起来不是很简单，而且我的 Typora 已经开始卡了，要不先停一停。

Examples

「LG P5829」【模板】失配树

用本文的语言来描述一下这个题：给定字符串 \(s\)，进行 \(m\) 次询问。每次询问给出 \(p,q\)，求 \(\max\{|b||b\in \Bord(p)\cap \Bord(q)\}\)。

---

用树来表示 \(\Bord()\) 的结构，这就不难发现询问求的就是 \(p\) 和 \(q\) 在树上的 LCA。

于是，按照这道题的本意，我们已经“完美地”解决了问题，复杂度为 \(O((|s|+m)\log |s|)\)。

---

不过，我们既然已经知道了数值上 Border 的等差结构，我们就可以用好这个信息来简化流程。

说简单一点，我们直接按照等差数列来划分树链，并模拟重链剖分的形式在树上蹦跶。这样即可保证最终跳 \(O(\log |s|)\) 次。

于是我们需要解决的问题便来了：

• 如何根据当前的位置，确定链头和公差？

  首先确定如何划分链。由于链的端点可能被包含在若干条链中，因此我们将链底保存在链中，而将链头排除在链之外。换句话说，也就是按照深度左开右闭。

  假设现在的位置是 \(k\)，那么公差自然是 \(\delta = k - \nxt_k\)。

  这里有两种情况，一者如果 \(\nxt_k\le \lfloor\frac k 2\rfloor\)，那么等差数列其实只有一项；否则，根据 Periodicity Lemma，我们可以得到链头应当为 \(k\bmod \delta + \delta\)，因为“链头” \(k\bmod \delta\) 不应当算在链内。当然，这种划分方式也很好地处理了 \(k\bmod \delta=0\) 的特殊情况。

• 如何移动两个点？

  按照重链剖分的理论，合理的跳法应该是选择终点较深的一个点跳。

  不过，由于原先 \(1,2,\dots,n\) 的顺序就是树的 DFS 序，所以我们暴力一步一步跳 \(\nxt\) 的时候，的确可以每次移动 DFS 序较大的一个点。于是“合理”的迁移就是，能不能每次将编号较大的一个点移到链头？

  不妨假设我们要移动 \(p\)，所以有 \(p>q\)。如果 \(p\) 不会跳过 \(lca\) 还好说。否则假设 \(p\) 会跳过 \(lca\)，也就是说：

  • 情况 1：\(q\) 就是 \(lca\)。

    这个比较容易。我们可以发现此时 \(q-\nxt_q=p-\nxt_p\)，它们同属一条链。

  • 情况 2：\(q\) 不是 \(lca\)。我们先来画个图：

    

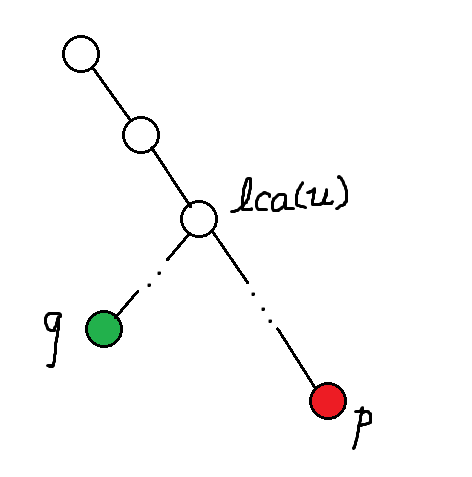
    为了方便，我们就用 \(u\) 指代 \(lca\)。条件告诉我们 \(u-\nxt_u=p-\nxt_p>q-\nxt_q\)。根据 KMP 算法流程，我们可以知道 \(k-\nxt_k\) 是随 \(k\) 增大而单调不降的量，因此这种情况是不存在的。

    ---

    2022.04.06 更新

    上面这个部分其实可以更简洁。我们注意到一定有 \(u\le q<p\)，而如果会跳过，则应该有 \(u-\nxt_u=p-\nxt_p\)。根据 \(k-\nxt_k\) 随 \(k\) 单调不降的性质，我们可以得出 \(q-\nxt_q=p-\nxt_p\)，所以跳过的情况一定意味着 \(q,p\) 共链。

  所以我们只需要在跳点的过程中判断一下是否会出现情况 1 即可。

最终复杂度为 \(O(n+m\log n)\)。实现代码无比简洁，并且跑得飞快。