[HDU 6598]Harmonious Army

题目

点这里看题目。

分析

首先由于每个士兵有两种选择，因此我们考虑最小割。

但是，与一般的最小割问题不同，不论士兵怎么搭配都会有贡献。为了进一步思考，我们不妨画出常见的基本图：

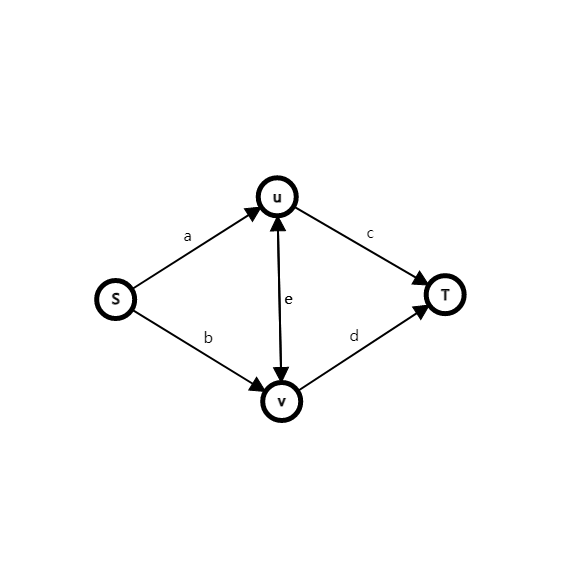
假如 \(u\in S\) 表示 \(u\) 作为战士， \(u\in S\) 表示 \(u\) 作为法师。

假如我们最初计算了所有贡献 \(A+B+C\) ，那么考察所有的割，应该有如下成立：

\[\begin{cases} a+b=A+B\\ c+d=B+C\\ a+e+d=A+C\\ b+e+c=A+C \end{cases} \]

自然， 4 个方程解不出来 5 个未知数，不过我们可以得到如下解：

\[\begin{cases} a=b=\frac{A+B}{2}\\ c=d=\frac{B+C}{2}\\ e=\frac{A+C}{2}-B \end{cases} \]

对着这组解建图即可。由于分母全是 2 ，因此可以对所有容量扩大两倍建图，最后再除回去。

小结：

这个例子告诉我们，最小割的基本模型中，容量本身是可以被直接代数构造（并提供了一组通解），而没有必要人脑构造。

代码

#include <cstdio>

typedef long long LL;

#define int LL

const LL INF = 0x3f3f3f3f3f3f3f3f;
const int MAXN = 1e5 + 5, MAXM = 1e5 + 5;

template<typename _T>
void read( _T &x )
{
    x = 0; char s = getchar(); int f = 1;
    while( s < '0' || '9' < s ) { f = 1; if( s == '-' ) f = -1; s = getchar(); }
    while( '0' <= s && s <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar(); }
    x *= f;
}

template<typename _T>
void write( _T x )
{
    if( x < 0 ) putchar( '-' ), x = -x;
    if( 9 < x ) write( x / 10 );
    putchar( x % 10 + '0' );
}

template<typename _T>
_T MIN( const _T a, const _T b )
{
    return a < b ? a : b;
}

struct Edge
{
    int to, nxt, c;
}Graph[MAXM << 1];

int q[MAXN];

int head[MAXN], dep[MAXN], cur[MAXN];
int N, M, cnt = 1, tot;

void AddEdge( const int from, const int to, const int C )
{
    Graph[++ cnt].to = to, Graph[cnt].nxt = head[from];
    Graph[cnt].c = C, head[from] = cnt;
}

void AddE( const int from, const int to, const int C ) { AddEdge( from, to, C ), AddEdge( to, from, 0 ); }

bool BFS( const int S, const int T )
{
    int h = 1, t = 0, u, v;
    for( int i = 1 ; i <= tot ; i ++ ) dep[i] = INF;
    dep[q[++ t] = S] = 0;
    while( h <= t )
    {
        u = q[h ++];
        for( int i = head[u] ; i ; i = Graph[i].nxt )
            if( Graph[i].c && dep[v = Graph[i].to] > dep[u] + 1 )
                dep[q[++ t] = v] = dep[u] + 1;
    }
    return dep[T] < INF;
}

int DFS( const int u, const int lin, const int T )
{
    if( u == T ) return lin;
    int used = 0, ret, v, c;
    for( int &i = cur[u] ; i ; i = Graph[i].nxt )
    {
        v = Graph[i].to, c = Graph[i].c;
        if( dep[v] == dep[u] + 1 && c && ( ret = DFS( v, MIN( lin - used, c ), T ) ) )
        {
            used += ret, Graph[i].c -= ret, Graph[i ^ 1].c += ret;
            if( used == lin ) break;
        }
    }
    if( used < lin ) dep[u] = INF;
    return used;
}

int Dinic( const int S, const int T )
{
    int f = 0;
    while( BFS( S, T ) )
    {
        for( int i = 1 ; i <= tot ; i ++ ) cur[i] = head[i];
        f += DFS( S, INF, T );
    }
    return f;
}

void Clean()
{
    cnt = 1, tot = N;
    for( int i = 1 ; i <= tot + 2 ; i ++ )
        head[i] = dep[i] = cur[i] = 0;
}

signed main()
{
    while( ~ scanf( "%lld %lld", &N, &M ) )
    {
        Clean(); LL ans = 0;
        const int s = ++ tot, t = ++ tot;
        for( int i = 1 ; i <= M ; i ++ )
        {
            int u, v, a, b, c;
            read( u ), read( v ), read( a ), read( b ), read( c );
            a <<= 1, b <<= 1, c <<= 1;
            ans += a + b + c;
            AddE( s, u, ( a + b ) >> 1 );
            AddE( s, v, ( a + b ) >> 1 );
            AddE( u, t, ( b + c ) >> 1 );
            AddE( v, t, ( b + c ) >> 1 );
            AddE( u, v, ( ( a + c ) >> 1 ) - b );
            AddE( v, u, ( ( a + c ) >> 1 ) - b );
        }
        write( ( ans - Dinic( s, t ) ) >> 1 ), putchar( '\n' );
    }
    return 0;
}