网络流理论基础

最大流

基础知识

下面一切基础知识都是为求出最大流而服务的。

以 定义（ \(\text D\) ）和 引理、定理、结论、推论（ \(\text T\) ）的形式呈现。

1. （ \(\text D\) ）网络 Network ：网络是一个有向图 \(G=(V,E)\) ，对于每一条边，有一个容量 capacity \(c(u,v)\) 。同时在图中还有两个特殊点 \(s,t\) ，一个叫源点一个叫汇点。

   注意在网络中我们不考虑负容量，我们总认为 \(c(u,v)\ge 0\) 。

   注意在网络中我们不考虑反向边，如果有反向边我们也可以拆开，就没有反向边了：

   

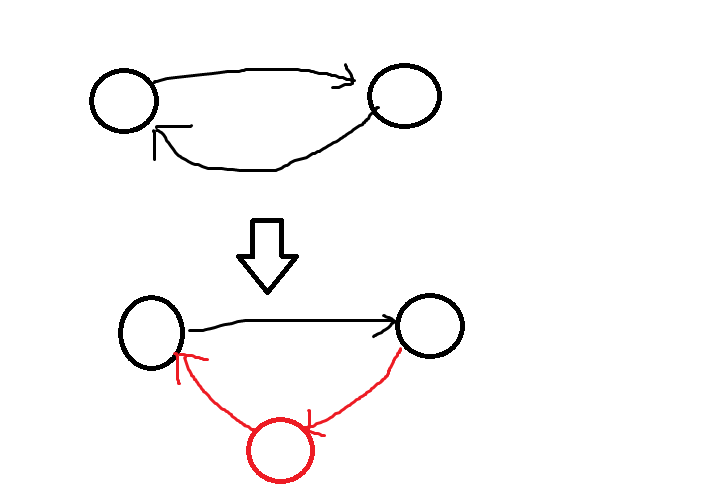
2. （ \(\text D\) ）可行流 Flow ：一个流给每一条边提供了一个函数值 \(f(u,v)\) ，当满足如下条件时，它是可行流：

   性质一：容量限制 \(\forall (u,v)\in E,0\le f(u,v)\le c(u,v)\)

   性质二：流量守恒 \(\forall v\in V-\{s,t\},\sum_{(u,v)\in E}f(u,v)=\sum_{(v,w)\in E}f(v,w)\)

   网络可以想象为一个排水系统（此处应有 [NOIP2020] ），其中 \(s\) 为一个大水库， \(t\) 就是一个大池塘，我们可以通过带有每秒流量上限的管道将水从 \(s\) 运输到 \(t\) 。一个流的两个限制等价于水管不能爆，且中间的节点不能存水。

   我们可以接着定义可行流的流量 \(|f|\) 为 \(s\) 流出的净流，也即：

   \[|f|=\sum_{(s,u)\in E}f(s,u)-\sum_{(v,s)\in E}f(v,s) \]

   此时我们就知道了最大流为网络上的最大可行流。

3. （ \(\text D\) ）残留网络 Residual Network ：这是对于原图 \(G\) 和 \(G\) 上的任意可行流 \(f\) 定义的。我们定义 \(G_f=(V_f,E_f)\) 为：

   • \(V_f=V\)
   • \(E_f=\{(u,v)|(u,v)\in E\lor (v,u)\in E\}\)
   • \(c_f(u,v)=\begin{cases}c(u,v)-f(u,v)&(u,v)\in E\\f(v,u)&(v,u)\in E\end{cases}\)

   可以发现，我们在残留网络中引入了反向边，但是仍然强调原图中是没有反向边的。

   当然，可以发现残留网络也是一个网络，所以说上面也有可行流。于是就有了下面的定义及性质：

4. （ \(\text D\) ）流的加法：对于 \(G\) 上的可行流 \(f\) 和 \(G_f\) 上的可行流 \(f'\) ，我们定义 \(g=f+f'\) 在原图上的流为：

   \[g(u,v)=f(u,v)+f'(u,v)-f'(v,u) \]

   此时反向边可以理解为 " 退流 " 。虽然直观上很好理解，但我们仍有必要证明一下 \(g\) 也是可行流：

5. （ \(\text T\) ）对于 \(G\) 上的可行流 \(f\) 和 \(G_f\) 上的可行流 \(f'\) ，\(g=f+f'\) 是原图的可行流：

   性质一

   根据可行流的定义，对于原图上任意的 \((u,v)\in E\)，有：

   \[\begin{cases} 0\le f'(u,v)\le c(u,v)-f(u,v)\\0\le f'(v,u)\le f(u,v) \end{cases} \]

   根据第二条有 \(f(u,v)-f'(v,u)\ge 0\) ，再根据 \(f'(u,v)\ge 0\) 可以推出 \(g(u,v)\ge 0\) 。

   根据第一条有 \(f(u,v)+f'(u,v)\le c(u,v)\) ，再根据 \(f'(v,u)\ge 0\) 可以推出 \(g(u,v)\le c(u,v)\) 。

   可知流 \(g\) 满足性质一。

   性质二

   对于 \(f'\) 有：

   \[\forall u\in V,\sum_{(v,u)\in E}f'(v,u)+\sum_{(u,w)\in E}f'(w,u)=\sum_{(u,w)\in E}f'(u,w)+\sum_{(v,u)\in E}f'(u,v) \]

   移项之后有：

   \[\forall u\in V,\sum_{(v,u)\in E}f'(v,u)-f'(u,v)=\sum_{(u,w)\in E}f'(u,w)-f'(w,u) \]

   然后加到 \(f\) 上面就能发现 \(g\) 也是守恒的。

   综上可知 \(g\) 是可行流。

   这个性质告诉我们，如果 \(G_f\) 上面有 \(|f'|>0\) 的可行流 \(f'\)，那么 \(f\) 一定不是 \(G\) 的最大流 。

6. （ \(\text D\) ）增广路 Augmenting Path ：

   对于任意网络上的一条从 \(s\) 到 \(t\) 的路径 \(P\) ，定义它的容量 \(\delta(P)=\min\{c(u,v)|(u,v)\in P\}\) 。

   增广路 \(A\) 要求 \(A\) 是一条 \(s\) 到 \(t\) 的路径 \(P\) 且 \(\delta(P)>0\) 。

   本质上增广路就是一种最简单的可行流。结合性质 5 可以发现，最大流 \(f\) 的 \(G_f\) 上也不会有增广路。

   此时困扰我们的问题就是：对于 \(G\) 上的可行流 \(f\) ，如果 \(G_f\) 上不存在增广路， \(f\) 是否是最大流？我们还无法断言，因为有可能我们会陷入局部最优解。为了解决这个问题，我们将要引入割这个概念。

7. （ \(\text D\) ）鸽咕咕咕 割 Cut ：网络上的一个割定义为对于点集 \(V\) 的一个划分 \([S,T]\) 。它们需要满足：

   性质一： \(S\cup T=V,S\cap T=\varnothing\)

   性质二：\(s\in S,t\in T\)

   注意 \(S\) 和 \(T\) 并不需要各自内部联通。因此一个网络的割的划分数为 \(2^{n-2}\) 。

8. （ \(\text D\) ）割的容量：定义 \(G\) 的一个割 \([S,T]\) 的容量为：

   \[c(S,T)=\sum_{u\in S}\sum_{v\in T}[(u,v)\in E]c(u,v) \]

   为了方便，我们也可以认为 \((u,v)\not \in E\Rightarrow c(u,v)=0\) 。因此上式可以简化。

   此时我们知道了最小割为网络上的最小容量割。

9. （ \(\text D\) ）割的流量：定义 \(G\) 的一个割 \([S,T]\) 对于 \(G\) 上任意一个可行流 \(f\) 的流量为：

   \[f(S,T)=\sum_{u\in S}\sum_{v\in T}f(u,v)-\sum_{u\in S}\sum_{v\in T}f(v,u) \]

   注意这里的定义是不对称的。割的容量只考虑正向边，而割的流量同时考虑正向和反向边。

   显然有 \(f(S,T)\le c(S,T)\) 。

   仔细思考我们不难提出如下猜想：是否有 \(|f|=f(S,T)\) ？

   感性理解是很自然的，对于任意一个割，我们将 \(S\) 分为与 \(s\) 相通的 \(S_c\) 和不相通的 \(S_c'\) 。那么 \(S_c'\) 的部分流量守恒，而 \(S\) 流到 \(T\) 流必然会经过 \(S_c\) 到 \(T\) 的边。下面我们将一步步证明这一点。

10. （ \(\text D\) ）任意点集的流量：定义 \(G\) 上的任意两个点集 \(X,Y\) 对于任意一个可行流 \(f\) 的流量为：

    \[f(X,Y)=\sum_{u\in X}\sum_{v\in Y}f(u,v)-\sum_{u\in X}\sum_{v\in Y}f(v,u) \]

    这个定义存在如下性质：

11. （ \(\text T\) ）对于 \(G\) 上的任意两个点集 \(X,Y\) 和任意一个可行流 \(f\) ， \(f(X,Y)\) 存在如下性质：

    性质一

    \[f(X,X)=0 \]

    证明略。

    性质二

    \[f(X,Y)=-f(Y,X) \]

    证明也略。

    性质三

    当 \(Y\cap Z=\varnothing\) 时，存在：

    \[f(X,Y\cap Z)=f(X,Y)+f(X,Z) \]

    这是因为 \(X\) 流向 \(Y\) 的流量和 \(X\) 流向 \(Z\) 的流量一定不会有重复计算。

12. （ \(\text T\) ）割的流量与流的流量：对于 \(G\) 上的任意一个割 \([S,T]\) 和任意一个可行流 \(f\) ，存在性质：\(|f|=f(S,T)\) 。

    证明：

    首先有 \(|f|=f(\{s\},V)\) 。

    而 \(f(S,V)=f(\{s\},V)+f(S-\{s\},V)\) 。

    注意到 \(S-\{s\}\) 里面的点都满足流量守恒，因此有 \(f(S-\{s\},V)=0\) 。

    于是 \(|f|=f(S,V)\) 。

    又有 \(f(S,V)=f(S,S\cup T)=f(S,S)+f(S,T)=f(S,T)\) 。

    因此 \(|f|=f(S,T)\) 。

    可以发现我们的猜想中已经把证明口胡过一遍了。

    结合定义 9 中提到的，有 \(|f|\le c(S,T)\) 。下面我们将要证明最大流最小割定理！

13. （ \(\text T\) ）最大流最小割定理 Maximum-flow-minimum-cut Theorem ：对于网络 \(G\) 和 \(G\) 上的一个可行流 \(f\)，以下三个命题是等价的：

    \((1)\) \(f\) 是最大流

    \((2)\) \(G_f\) 上不存在的增广路

    \((3)\) \(\exists [S,T],|f|=c(S,T)\)

    证明：

    首先思考一下我们证明的方式，我们可以证明 \((1)\Rightarrow (2),(2)\Rightarrow (3),(3)\Rightarrow (1)\) ，这样便可以说明三个命题是等价的。

    证明 \((1)\Rightarrow (2)\)：

    请回头查看定义 6 。

    证明 \((2)\Rightarrow (3)\)：

    此时我们进行构造证明：

    构造 \(S\) 为在 \(G_f\) 上从 \(\{s\}\) 出发，仅经过容量为正的边能到达的点的集合，那么 \(T\) 即为 \(V-S\) 。

    由于 \(G_f\) 上没有增广路，所以 \(t\not\in S\) ，所以 \([S,T]\) 构成了 \(G\) 的一个割。

    我们只需要证明 \(|f|=c(S,T)\) 。

    根据结论 12 中提到的，有 \(|f|=f(S,T)\) ，所以我们只需要证明 \(f(S,T)=c(S,T)\) 。

    根据 \(f(S,T)\) 的定义，这也就是证明 \(\forall u\in S,v\in T,f(u,v)=c(u,v);\forall v\in T,u\in S,f(v,u)=0\) 。

    首先考虑第一个部分，即 \(f(u,v)=c(u,v)\) 。

    利用反证法，如果 \(f(u,v)<c(u,v)\) ，那么 \(c(u,v)-f(u,v)>0\) ，在 \(G_f\) 上 \((u,v)\) 的容量为正，那么 \(v\) 应该属于 \(S\) ，矛盾。所以 \(f(u,v)=c(u,v)\) 。

    类似的，如果 \(f(v,u)>0\) ，那么在 \(G_f\) 上，就会有 \((u,v)\) 的容量为正，那么 \(v\) 应该属于 \(S\) ，矛盾。所以 \(f(v,u)=0\) 。

    因此我们就证明了 \((2)\Rightarrow (3)\) 。

    证明 \((3)\Rightarrow (1)\)：

    我们使用夹逼法。别想歪了

    根据结论 12 我们可以知道 \(|f|\le c(S,T)\) ，即：

    \[\begin{aligned} &\max_f\{|f|\}\le c(S,T)=|f|\\ \Rightarrow &\max_f\{|f|\}\le |f| \end{aligned} \]

    而又有 \(|f|\le \max_{f}\{|f|\}\) ，所以 \(\max_{f}\{|f|\}=|f|\) 。即 \(f\) 是最大流。

    证毕！

14. （ \(\text T\) ）这是根据最大流最小割定理的得到的推论，但是是其最常用的形式。即对于任意网络 \(G\) 有：

    \[\max_f\{|f|\}=\min_{[S,T]}\{c(S,T)\} \]

    证明：

    结合最大流最小割定理，我们知道对于最大流 \(f\) ，\(\exists [S,T],|f|=c(S,T)\) 。

    我们只需要说明 \([S,T]\) 是最小割。

    类似地，有 \(|f|=c(S,T)\le \min_{[S,T]}\{c(S,T)\}\) 和 \(\min_{[S,T]}\{c(S,T)\}\le c(S,T)\) ，所以 \([S,T]\) 是最小割。

至此我们关于最大流的理论知识也就差不多结束了。

求解最大流

求解网络最大流有两种方法：增广法和预流推进法。

增广法

又被称为 FF, Ford-Fulkerson 方法，直接基于最大流最小割定理——也就是反复迭代直到在残留网络中找不到增广路为止。

以下算法都基于这个思想。笔者将它们按照时间复杂度上界来排序。

Ford-Fulkerson 算法

该算法每次寻找一条增广路并沿着增广路推流，维护过程结束后的残留网络。

如果每次使用 DFS 搜索，时间复杂度是 \(O(|E|F)\) 的，其中 \(F\) 为图的最大流的流量。

不过据说该算法还有改进版，叫做 Scaling Max-flow Algorithm ，还有一篇国内搜出来短得离谱的论文。确实没看懂是什么意思。

Scaling Max-flow Algorithm 在这篇博客里有提到。

Edmonds-Karp 算法

该算法思想同上，唯一的区别是确定了搜索增广路的顺序：它每次搜索最短的增广路，可以采用 BFS 实现。

经过这样的改变，时间复杂度下降到了 \(O(|V||E|^2)\) 。关于其复杂度的证明可以参考这篇博客。

Dinic 算法

该算法对 EK 进行了改进，每次对最短的增广路进行多路增广。

算法流程不难理解。每次迭代过程中，为了走到最短的增广路，算法会首先从 \(s\) 出发进行一次 BFS 对图进行分层。实际上我们得到了 \(d(u)\) ，为从 \(s\) 出发到达 \(u\) 的最少边数。

接着进行多路增广。根据最短路性质，如果 \((u,v)\in E\) ，那么 \(d(u)+1\le d(v)\) 。如果 \(d(u)+1=d(v)\) 则说明 \(u\) 在从 \(s\) 到 \(v\) 的一条最短路上——也就是说我们从 \(u\) 向 \(v\) 增广是合法的。

所以算法会再进行一次 DFS ，根据 \(d\) 的信息进行搜索，途中维护路径上的边的最小容量。这样我们每搜索到 \(t\) 的一次，我们就得到了一条增广路。回溯过程中可以顺便维护一下增广后的残留网络。

Dinic 的时间复杂度是 \(O(|V|^2|E|)\) 的，来源于每次 DFS 增广的 \(O(|V||E|)\) 和 \(O(|V|)\) 的层数上界。

Dinic 还有一个重要的优化：当前弧优化。

当前弧优化即指，如果一条边已经满流，那么之后就没有必要再搜索它了。优化点在于，由于每个点可能会被增广很多次，所以每次遍历的边的数量会减少。

ISAP 算法

改进版最短增广路算法 Improved Shortest Augmenting Path 。大概是说在 DFS 的过程中直接维护 Dinic 的 \(d\) 这个分层标号，而不是每次再用 BFS 进行分层。优化空间貌似很大。实际上还不会。

预流推进法

考虑一个相当直接的方法：我们可以首先给 \(s\) 一个无穷大的流量，然后尝试通过边把 \(s\) 的流量给推出去，直到我们将流推到了 \(t\) 。最后当我们没法推流的时候，我们就找到了最大流。

HLPP 算法

最高标号预流推进法 Highest Label Pre-flow Push 。还不会。

求解最小割

根据最大流最小割定理，我们可以建完图之后直接跑最大流算法得到最小割。

根据最大流最小割定理的证明过程，我们也很容易构造出一个合法的最小割（如果此时你还不会，请回到定理 \(13\) 的证明）。

需要注意的是，由于网络中的流量总是非负，建图的时候一定一定注意不要建立负容量的边！如果出现了这种情况，那么一定要仔细检查自己的思路是否正确。

费用流

基础知识

费用流问题的背景是一个网络 \(G=(V,E)\) ，对于每条边 \((u,v)\) 除了容量外，还有额外的正费用 \(w(u,v)\) 。

对于可行流 \(f\) ，我们定义它的费用：

\[w(f)=\sum_{(u,v)\in E}f(u,v)\times w(u,v) \]

对于可行流 \(f\) ，我们定义它的残余网络 \(G_f=(V_f,E_f)\) ，其中：

• \(V_f=V\) ;

• \(\forall (u,v)\in E_f,(u,v)\in E\lor (v,u)\in E\) ；

• 容量和权：

  \[\begin{aligned} c(u,v)&= \begin{cases} c(u,v)-f(u,v)&(u,v)\in E\\ f(v,u)& (v,u)\in E\\ \end{cases} \\ w(u,v)&= \begin{cases} w(u,v)&(u,v)\in E\\ -w(v,u)& (v,u)\in E\\ \end{cases} \\ \end{aligned} \]

通常我们解决的是最小费用最大可行流问题，该问题便是求在 \(|f|\) 最大时， \(w(f)\) 的最小值。

求解费用流

SSP 方法

SSP 方法全称为 Successive Shortest Path 方法，即 " 连续最短路 " 方法。

顾名思义，我们每次从 \(s\) 出发，以 \(w\) 作为边权搜索一条到达 \(t\) 的最短路，并沿着最短路增广。当我们无法增广的时候算法结束。

看起来非常正确，以下给出正确性证明。

证明

最大流部分：

显然，如果不存在最短增广路即等价于 \(s\) 无法到达 \(t\) ，根据最大流部分的知识，即不存在增广路，那么最终得到的一定是最大流。

最小费用部分：

• 引理：

  定义 \(F_i\) 为所有流量为 \(i\) 的可行流的集合。则 \(w(f)=\min_{f'\in F_{|f|}}\{w(f')\}\) \(\Leftarrow\) \(G_f\) 中没有负圈。

  为了方便，以下简称左半陈述为 " \(f\) 是最小费用流 " 。

  证明

  假设 \(G_f\) 不存在负圈，但是 \(f\) 却不是最小费用流。

  找出费用更小的一个流 \(f'\) ，比较这两个流。

  由于 \(|f|=|f'|\) ，并且对于 \(u\in V-\{s,t\}\) ， \(u\) 在两个流中都满足流量守恒，所以 \(f\) 和 \(f'\) 的差异必然形成了多个内部流量抵消的圈。由于 \(w(f')<w(f)\) ，所以这些圈内必然有一个总费用为负，即存在负权圈。

  对于差异中的任何一条边 \((u,v)\) ，我们可以说明它必然存在于 \(G_f\) 上：

  • 如果 \(f(u,v)>f'(u,v)\) ，则可以看作是退流。由于 \(f(u,v)>f'(u,v)\ge 0\) ，所以 \((v,u)\in E_f\) 。
  • 如果 \(f(u,v)<f'(u,v)\) ，则可以看作是推流。由于 \(f(u,v)<f'(u,v)\le c(u,v)\) ，所以 \((u,v)\in E_f\) 。

  所以 \(G_f\) 上必定存在负圈，矛盾。因此成立。

• 正确性证明：

  对于构造过程中的任何一个流 \(f\) ，我们证明它一定是最小费用流。

  一开始，流量为 0 ，并且 \(w\) 均为正，因此 \(G_f\) 中没有负圈。

  中途过程进行反证法，假设 \(G_f\) 存在负圈，考虑两种情况：

  • \(G_f\) 里面的负圈新出现于上一步增广。由于圈上总和为负，因此增广路上总和为正，显然我们可以不走这个圈得到一条更短的路径，矛盾；
  • \(G_f\) 里面的负圈在上一步的残余网络里面。由于初始没有负圈，因此负圈一定由增广得到，矛盾；

  因此 \(G_f\) 里面不可能存在负圈，也即 \(f\) 是最小费用流。

类 Edmonds-Karp 算法

类似于 Edmonds-Karp ，每次不使用 BFS 而是最短路算法寻找增广路。时间复杂度为 \(O(|V||E|F)\) ，其中 \(F\) 为最大流的流量。

类 Dinic 算法

类似于 Dinic ，每次不使用 BFS 而是最短路算法进行分层。在搜索过程中也依靠边权确定是否合法跨层。

中途需要注意标记节点是否已经经过，避免因为 \(w=0\) 的边而搜出环。

时间复杂度退化为 \(O(|V||E|F)\) ， \(F\) 意义同上。原因竟是分层现在没有层数上限了。

类 ISAP 算法

不清楚，这是我刚刚编出来的

zkw 算法

这是由 zkw 发明的费用流算法，先引用一段有趣的故事：

最小费用流在 OI 竞赛中应当算是比较偏门的内容, 但是 NOI2008 中 employee 的突然出现确实让许多人包括 zkw 自己措手不及. 可怜的 zkw 当时想出了最小费用流模型, 可是他从来没有实现过, 所以不敢写, 此题 0 分. zkw 现在对费用流的心得是: 虽然理论上难, 但是写一个能 AC 题的费用流还算简单. 先贴一个我写的 costflow 程序: 只有不到 70 行, 费用流比最大流还好写～。

没有代码，这篇博客里不放代码。

大概过程：增广部分类似于 Dinic/ISAP ，而标号部分类似于 KM 。

具体过程：还没学会

番外：最短路算法

通常，我们处理负权最短路的时候，使用的都是 Bellman-Ford 或者 SPFA 。

但是如果你愿意，可以采用类似于 Johnson 算法的科技，给每个点加权从而消除负权边。这样你就可以使用 Dijkstra 了。

番外：负权边

注意到证明过程中我们只限制了 \(G\) 上面没有负圈，因此，当我们使用基于最短路算法的费用流算法的时候，我们可以接受负权边，只需要初始的图上不存在负圈。

但是在使用 zkw 算法的时候，图上绝对不能出现负权边，可能是因为 KM 标号过程中的限制，处理负权边的方法可以参考使用 Dijkstra 的方法。

虽然有负圈我们不能单纯地 SSP 迭代出答案，但是这并不意味着这种情况下没有最小费用最大流，只不过这个过程中我们需要做一些改变，具体操作请参考其它博客。