[CF1063F]String Journey
题目
点这里看题目。
分析
以下标记子串的方法为: \(S[l,r]\) 表示 \(S\) 中从 \(l\) 到 \(r\) 的字符组成的子串。用 ( 表示开区间, [ 表示闭区间。
我们不难想到一个 DP :
\(f(i,k)\):以 \(i\) 开始的后缀,结尾字符串长度为 \(k\) 时的最长的 \(\mathcal{Journey}\) 。
然后观察并且感性理解一下就会发现,一个最优 \(\mathcal{Journey}\) 里面,一定有 \(t_i\) 仅仅比 \(t_{i+1}\) 多一个字符。
显然我们对于任意一个合法的 \(\mathcal{Journey}\) 都可以经过调整满足这个性质,而满足这个性质就会让 \(\mathcal{Journey}\) 更短,因而会更有机会变长。
你就感性一下就好
于是重新定义状态有:
\(f(i)\):以 \(i\) 开始的后缀中最长的 \(\mathcal{Journey}\) 。
考虑怎么转移。我们可以枚举一个 \(j\) 。如果说可以转移,那么此时 \(f(i)=f(j)+1\) ,且应该有:
也就是说, \(S[j,j+f(j))\) 是 \(S[i,i+f(i))\) 的子串。
这样做可以用 Hash 方法优化到 \(O(n^2)\) 。
进一步考虑这个问题。注意一下 \(f(i)\) 和 \(f(i+1)\) 的关系:
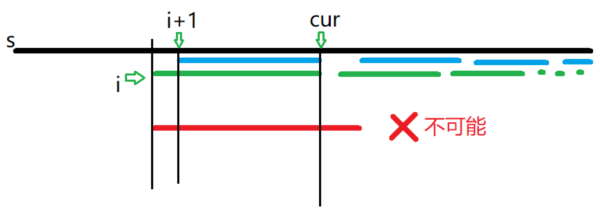
可以发现 \(f(i)\le f(i+1)+1\) ,否则 \(f(i+1)\) 就应该更大。
假如我们用一个指针 \(cur\) 来标记我们现在可以转移的边界。那么 \(cur\) 就应该是单调不增的。
如果说当前位置为 \(f(i)\) ,而我们发现 \(f(i)=cur-i+1\) 的时候没有办法转移,我们就需要 cur -- 。
如何判断这个东西呢?转移位置 \(j\) 合法需要满足下列条件:
- \(s[i,i+f(i)-1)=s[j,j+f(i)-1)\ \lor\ s[i+1,i+f(i))=s[j,j+f(i)-1)\)。
- \(f(j)\ge f(i)-1\) 。
考虑第一个条件可以拆成两个串分别判断。此时应该有 \(s[i,i+f(i)-1)\) 是 \(s[j,n]\) 的前缀。我们可以理解为,对原串构建后缀自动机,满足第一个条件的所有 \(j\) ,其后缀 \(s[j,n]\) 必然在 \(s[i,i+f(i)-1)\) 的 fail 子树里面。
考虑第二个条件。结合前面的分析,我们可以将 \(f(j)\) 的值挂到 \(s[j,j+f(j))\) 对应的状态上,并且只需要查询 \(s[i,i+f(i)-1)\) 在 fail 树内的子树最大值进行判断便可。
综合来说,时间复杂度是 \(O(n\log_2n)\) 。
代码
#include <cmath>
#include <cstdio>
#include <cstring>
const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + 5, MAXLOG = 21;
template<typename _T>
void read( _T &x )
{
x = 0;char s = getchar();int f = 1;
while( s > '9' || s < '0' ){if( s == '-' ) f = -1; s = getchar();}
while( s >= '0' && s <= '9' ){x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar();}
x *= f;
}
template<typename _T>
void write( _T x )
{
if( x < 0 ){ putchar( '-' ); x = ( ~ x ) + 1; }
if( 9 < x ){ write( x / 10 ); }
putchar( x % 10 + '0' );
}
template<typename _T>
_T MAX( const _T a, const _T b )
{
return a > b ? a : b;
}
struct edges
{
int to, nxt;
}Graph[MAXN];
int seg[MAXN << 2];
int f[MAXN];
int fath[MAXN][MAXLOG];
int head[MAXN], DFN[MAXN], siz[MAXN];
int ch[MAXN][26], fa[MAXN], mx[MAXN], ed[MAXN];
int N, rt, tot, lst, ID, lg2, cnt;
char S[MAXN];
void copy( int a, int b ) { fa[a] = fa[b], mx[a] = mx[b], memcpy( ch[a], ch[b], sizeof ch[b] ); }
void addEdge( const int from, const int to )
{
Graph[++ cnt].to = to, Graph[cnt].nxt = head[from];
head[from] = cnt;
}
void insert( const char c )
{
int x = c - 'a', cur = ++ tot, p = lst;
mx[cur] = mx[lst] + 1, lst = cur;
while( p && ! ch[p][x] ) ch[p][x] = cur, p = fa[p];
if( ! p ) { fa[cur] = rt; return ; }
int q = ch[p][x];
if( mx[q] == mx[p] + 1 ) { fa[cur] = q; return ; }
int nq = ++ tot; copy( nq, q );
mx[nq] = mx[p] + 1, fa[cur] = fa[q] = nq;
while( p && ch[p][x] == q ) ch[p][x] = nq, p = fa[p];
}
void DFS( const int u )
{
siz[u] = 1, DFN[u] = ++ ID;
for( int i = head[u], v ; i ; i = Graph[i].nxt )
DFS( v = Graph[i].to ), fath[v][0] = u, siz[u] += siz[v];
}
void upt( const int x ) { seg[x] = MAX( seg[x << 1], seg[x << 1 | 1] ); }
void build( const int x, const int l, const int r )
{
if( l > r ) return ; seg[x] = -INF;
if( l == r ) return ;
int mid = l + r >> 1;
build( x << 1, l, mid );
build( x << 1 | 1, mid + 1, r );
}
void update( const int x, const int l, const int r, const int pos, const int v )
{
if( l == r ) { seg[x] = MAX( seg[x], v ); return ; }
int mid = l + r >> 1;
if( pos <= mid ) update( x << 1, l, mid, pos, v );
else update( x << 1 | 1, mid + 1, r, pos, v );
upt( x );
}
int query( const int x, const int l, const int r, const int segL, const int segR )
{
if( segL <= l && r <= segR ) return seg[x];
int mid = l + r >> 1, ret = -INF;
if( segL <= mid ) ret = MAX( ret, query( x << 1, l, mid, segL, segR ) );
if( mid < segR ) ret = MAX( ret, query( x << 1 | 1, mid + 1, r, segL, segR ) );
return ret;
}
void init()
{
for( int i = 2 ; i <= tot ; i ++ ) addEdge( fa[i], i );
DFS( 1 ), build( 1, 1, tot );
lg2 = log2( tot );
for( int j = 1 ; j <= lg2 ; j ++ )
for( int i = 1 ; i <= tot ; i ++ )
fath[i][j] = fath[fath[i][j - 1]][j - 1];
}
int locate( const int st, const int len )
{
int p = ed[st];
if( mx[p] < len ) return -1;
for( int i = lg2 ; ~ i ; i -- )
if( fath[p][i] && mx[fath[p][i]] >= len )
p = fath[p][i];
return p;
}
bool chk( const int st, const int len )
{
int p, val;
if( len == 1 ) return true;
if( ~ ( p = locate( st, len - 1 ) ) )
{
val = query( 1, 1, tot, DFN[p], DFN[p] + siz[p] - 1 );
if( val >= len - 1 ) return true;
}
if( ~ ( p = locate( st + 1, len - 1 ) ) )
{
val = query( 1, 1, tot, DFN[p], DFN[p] + siz[p] - 1 );
if( val >= len - 1 ) return true;
}
return false;
}
int main()
{
read( N ), scanf( "%s", S + 1 );
rt = lst = ++ tot;
for( int i = N ; i ; i -- ) insert( S[i] ), ed[i] = lst;
init();
f[N] = 1; int rig = N, ans = 1;
for( int i = N - 1 ; i ; i -- )
{
while( ! chk( i, rig - i + 1 ) )
{
update( 1, 1, tot, DFN[locate( rig, f[rig] )], f[rig] );
rig --;
}
f[i] = rig - i + 1;
ans = MAX( ans, f[i] );
}
write( ans ), putchar( '\n' );
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号