拉格朗日插值法入门

目录

• 什么是插值
• 拉格朗日插值法
• 拉格朗日插值法的应用
  • 多项式插值
  • DP 优化
  • 求自然数幂和
• 其它插值方法
  • 拉格朗日插值法改进版
  • 重心拉格朗日插值法

什么是插值

在离散数据的基础上补插连续的函数，使得这条连续函数经过所有离散数据点，这个过程就叫插值。

其意义在于：

插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。

你猜对了，以上均来自百度百科的 “ 插值 ” 词条。

怎么理解这个东西呢？举个例子，操场上有人在踢足球。球员一脚把球踢飞了，假设球始终在一个平面上运行，它的轨迹就可以抽象为一个函数$f(t)$（假设它只与与时间相关）。

现在，你借来了一台高速摄像机，拍下了很多张片照片，那么一张照片实际上就是得到了函数图像上的一个点 $(t_i,f(t_i))$。

插值就相当于，你知道了一些照片（离散的数据），想要还原出球的运动轨迹 $f(t)$。当然，由于你只可能有有限的照片，而函数是连续的，那么你只能去近似地还原函数。这也意味之，插值的结果 $g(t)$总是无穷多的。

插值有许多方法，包括：三角函数插值；线性插值法；牛顿插值法；拉格朗日插值法......

下面请出今天的主角——拉格朗日...插值法！拍肚皮拍肚皮拍肚皮......

拉格朗日插值法

拉格朗日插值法 ( Lagrange Interpolation Polynomial ) 是以十八世纪数学家约瑟夫·拉格朗日 ( Joseph-Louis Lagrange ) 命名的插值法，它可以根据已有离散数据得出多项式的差值结果。

它的思想非常简单，大概可以理解为——硬性配凑！

怎么配凑呢？我们举个例子，平面上有三个点， $(x_1,y_1),(x_2,y_2),(x_3,y_3)(x_1<x_2<x_3)$，我们现在用它们仨插值。

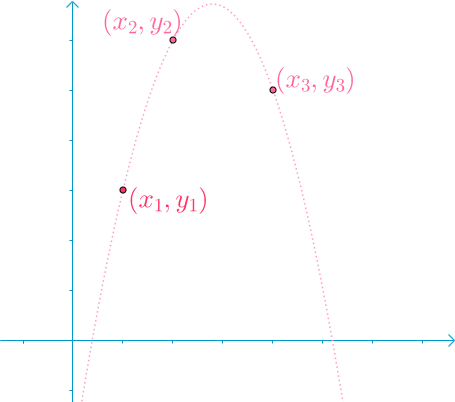
根据小学基础知识，我们知道，这三个点肯定可以唯一确定一个二次函数。

那么我们就尝试找到它，怎么找？拉格朗日想到了一个比较粗暴的方法——咱对于每个点都搞一个子函数 $f_i(x)$，要求 $f_i(x)$ 在 $x=x_i$ 的时候得到 $1$，在 $x=x_j(j\not=i)$ 的时候得到 $0$，把 $n$ 个子函数凑起来，得到的函数不就过了 $n$ 个点了！

也就是说，我们要计算 $n$ 个子函数，第 $i$ 个子函数为：

$$f_i(x)= \begin{cases} 1 & x=x_i\\ 0 & x=x_j(j\not=i)\\ I\ don't\ care & otherwise \end{cases}$$

那么插值的结果就是：

$$f(x)=\sum_{i=1}^n y_if_i(x)$$

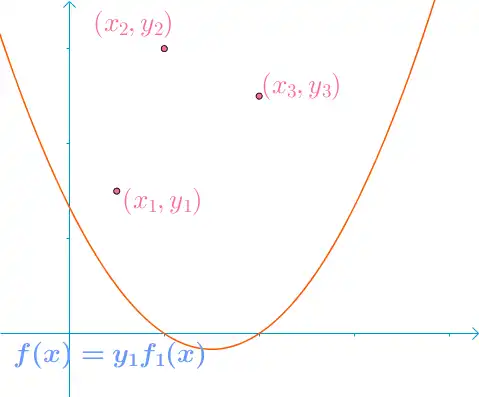
回到原问题上面来。考虑构造 $f_1(x)$，对于 $f_1(x_j)=0(j>1)$ 的情况很好满足，可以想到：

$$f_1(x)=(x-x_2)(x-x_3)$$

怎么让 $f_1(x_1)=1$ 呢？我们只需要把不用的丢掉就好：

$$f_1(x)=\frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}$$

所以最后就有 $f_1(x_1)$ 长成下面这个亚子：

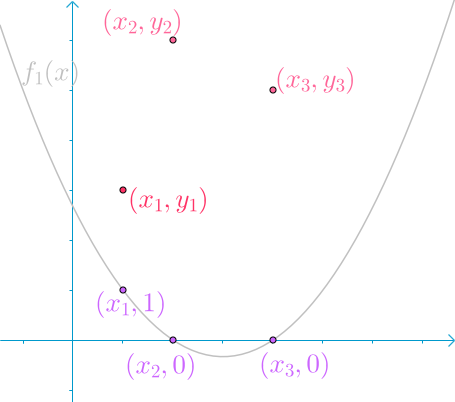
同理构造出 $f_2(x)$：

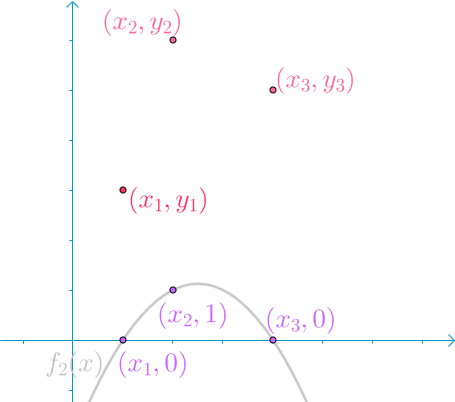
和 $f_3(x)$：

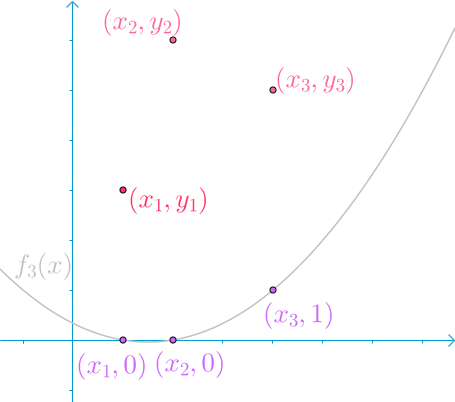
求和得到$f(x)$：

$$f(x)=\frac{y_1(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}+\frac{y_2(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}+\frac{y_3(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)}$$

也可以很方便地推广到一般形式：对于$n$个点$(x_1,y_1),(x_2,y_2),...,(x_n,y_n)(x_1<x_2<...<x_n)$，设：

$$f_i(x)=\frac{\prod_{j\not=i}(x-x_j)}{\prod_{j\not=i}(x_i-x_j)}$$

那么插值结果就是：

$$f(x)=\sum_{i=1}^ny_if_i(x)=\sum_{i=1}^ny_i\times \frac{\prod_{j\not=i}(x-x_j)}{\prod_{j\not=i}(x_i-x_j)}$$

模板LGP4781：

for( int i = 1 ; i <= N ; i ++ )
{
	fi = 1;
	for( int j = 1 ; j <= N ; j ++ )
		if( i ^ j )
			fi = 1ll * fi * fix( k - x[j] ) % mod * inv( fix( x[i] - x[j] ) ) % mod;
	ans = ( ans + 1ll * fi * y[i] % mod ) % mod;
}

拉格朗日插值法的应用

多项式插值

拉格朗日插值法可以直接用于离散数据的多项式插值，普通方法的时间复杂度是 $O(n^2)$，经过多项式膜法优化之后可以达到 $O(n\log_2^2n)$（没错，多项式快速插值就是从拉格朗日插值法优化来的）。

其实，如果不知道拉格朗日插值法，也可以使用一般方法进行多项式插值——直接上待定系数法，用高斯消元解方程组就可以。但是拉格朗日方法显然优点明显：

1. 快，快，快得多。高斯消元 $O(n^3)$，拉格朗日只有 $O(n^2)$，还可以优化至 $O(n\log_2^2n)$。

2.拉格朗日插值法支持取模，而高斯消元法......

3.还有很多优点，我这里就不一一列举了

不过，在实际应用中，拉格朗日插值法也存在一些缺点。比如说，如果离散数据是变化的，时不时就会多一个点或者少一个点，那么每次变化，拉格朗日插值法都需要重新计算一遍每一个子函数，导致效率非常非常低下。这个时候可以考虑采用易于处理这种情况的牛顿插值法或者拉格朗日插值法的改进版。

再比如，拉格朗日插值法的结果的次数与插值点数成正比。这就意味着，插值点多几个，拉格朗日插值法在非插值点的位置，就有可能会显出很大的偏差。（具体可以参考龙格现象）

DP 优化

这两个东西怎么会有关系呢？嗯？

它们确实有关系......

在一类计数 DP 中，如果判定 DP 可以被表示为关于状态内某个变量的多项式函数，那么我们就可以利用小范围的点值，插值得到函数，再代入题目所需的数据求解。

这种方法通常要求小范围的点值可以在时间限制内快速计算，但最关键的还是，要找出“ DP 为变量的多项式函数”这一性质，并且准确地猜测估计计算出函数的次数。

该方法的主要意义还是在于缩减数据范围，当规模小到可以直接计算，就直接计算，然后倒推回答案。

经典例题：[集训队互测]calc。

求自然数幂和

这个应用基于一个性质：设 $S_k(n)=\sum_{i=1}^ni^k$，那么 $S_k(n)$ 就一定可以被表示为一个关于 $n$ 的 $k+1$ 次多项式。

证明可以由自然数幂和的推导方式得来（比如差分法），或者使用数学归纳法，之类的。

然后，既然知道了这个结论，我们就直接用，求 $S_k(n)$ 的时候，我们先算出前 $k+2$ 项的幂和，然后就可以把 $n$ 代入求值。由于前 $k+2$ 个自然数是连续的一段整数，因此可以很方便地对插值过程中的系数进行递推。单次可以做到 $O(k\log_2p)$，其中 $p$ 为模数（需要存在逆元）。

题外话：求自然数幂和的方法不少，插值法之外还有 伯努利数 + 多项式膜法 ，第二类斯特林数 等等。

其它插值方法

拉格朗日插值法改进版

这个方法其实......就是对原先的式子稍微修改一下。

考察 $f_i(x)$ ：

$$\begin{aligned} f_i(x) &=\frac{\prod_{j\not=i}(x-x_j)}{\prod_{j\not=i}(x_i-x_j)}\\ &=\frac{\prod_{j=1}^n(x-x_j)}{(x-x_i)}\times \frac{1}{\prod_{i\not=j}(x_i-x_j)} \end{aligned}$$

经过这样的变换，我们发现每个子函数都有一大块是相似的，因此定义:

$$\ell(x)=\prod_{i=1}^n (x-x_j)$$

于是就有：

$$f_i(x)=\frac{\ell(x)}{(x-x_i)}\times \frac{1}{\prod_{i\not=j}(x_i-x_j)}$$

对 " 各具特色 " 的后半部分专门定义，称为重心权：

$$w_i=\frac{1}{\prod_{i\not=j}(x_i-x_j)}$$

于是我们就得到了拉格朗日公式改进版：

$$f(x)=\sum_{i=1}^n \ell(x)\frac{w_i}{(x-x_i)}$$

这个公式的优点在于，插值点多一个或者少一个，它就只会影响到共 $n$ 个值。而这 $n$ 个值的修改理论可以做到单个 $O(1)$，总的修改时间就是 $O(n)$ 。

重心拉格朗日插值法

待填坑