后缀自动机入门

什么是自动机

（有限状态）自动机是一种抽象的计算模型。一个有限状态自动机有有限个状态，每个状态可以迁移到一个或者多个状态。给定的字符串指定了如何转移。一个有限状态自动机可以表示为一个有向图。

对于一个自动机 \(S\)。如果对于一个串 \(A\)，经过转移之后停在了一个“接收状态”那么 \(A\) 就被 \(S\)“接受”了，记为 \(S(A)=T\)；否则如果停在了一个“拒绝状态”，那么 \(A\) 就被 \(S\)“拒绝”了，记为 \(S(A)=F\)。

后缀自动机

引子

后缀自动机就是对于一个串 \(S\) 建立的自动机 \(S'\) 。如果串 \(A\) 是 \(S\) 的后缀，那么 \(S'(A)=T\)；否则 \(S'(A)=F\)。

最暴力的方法，把所有的后缀插到一个 Trie 里面。时间空间都是——完美的 \(O(n^2)\)。

但是事实上，这颗 Trie 上面会有很多重复的部分，比如：

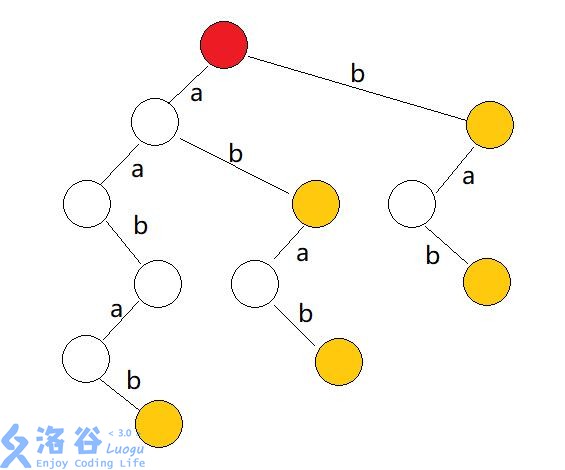
这上面 \("bab"\) 的部分就出现了三次，而我们实际上只需要它出现一次！

这样的现状让我们有了希望——构造一个边数和点数都最少的后缀自动机（此时它不是 Trie,而是一个 DAWG：有向无环字母图），或许它就是真正可用的呢！

前置知识

设 \(S\) 为一个要建立后缀自动机的串。\(S\) 的字符的下标从 0 开始。

1. 定义： \(\operatorname{end-pos}(A)\) 表示 \(A\) 在 \(S\) 中出现的右端点的集合。比如，\(S="aabbabd",A="ab"\)，则 \(\operatorname{end-pos}(A)=\{2,5\}\)。

   可以发现，Trie 上 \(\operatorname{end-pos}\) 相同的两个字符串，在它们后面添加字符之后，它们的 \(\operatorname{end-pos}\) 还是相同的。所以它们的出边肯定是一样的，所以可以合并。

   因此，一个没有 \(\operatorname{end-pos}\) 的相同的两个节点的后缀自动机被称为最简后缀自动机（一定是点数最少的，边数不确定）。

2. 定理：若 \(\operatorname{end-pos}(A)=\operatorname{end-pos}(B)\)，且不为空集，那么其中有一个就是另一个的后缀。

   说明

   如果有交集，就说明有一个是另一个的后缀，不妨设 \(A\) 是 \(B\) 的后缀。那么以后 \(B\) 每出现一次， \(A\) 也一定会出现一次。所以 \(\operatorname{end-pos}(B)\subset \operatorname{end-pos}(A)\)。

3. 定理： $\operatorname{end-pos} $ 相等的字符串，长度一定组成一个连续的区间。

   举个例子，对于 \(S="aabbabd"\)，\(\operatorname{end-pos}("bb")=\operatorname{end-pos}("abb")=\operatorname{end-pos}("aabb")\)，它们的长度组成了区间 \([2,4]\)。

   可以利用前面的定理 2 反证。

4. 定义：在后缀自动机上面，对于一个节点 $ u $ ，每一个从自动机的起始状态到 $ u $ 的路径可以视作一个字符串，我们称这些字符串为 $ u $ 表示的字符串。设 \(\text{mn}_u\) 表示这之中长度最短的， \(\text{mx}_u\) 表示这之中最长的。

5. 定义：后缀链接：对于一个节点 $ u $，它所表示的字符串的 $\operatorname{end-pos} $ 都是一样的。而存在一个节点 $ v $，满足所有 $ v $ 表示的字符串均是 $ u $ 表示的串的后缀，并且 \(\text{mx}_v=\text{mn}_u+1\)。

   我们记 $ v=\text{fa}_u $，这就是后缀自动机上面的 $ \text{fa} $ 边的来源。显然，这样的节点还保证 $ \operatorname{end-pos}(u)\subset \operatorname{end-pos}(v) $。所以如果我们沿着 $ \text{fa} $ 往上跳，我们可以走到的位置是只增不减的。

6. 定理：根据性质 2，\(\text{fa}\) 必然构成了一颗树，我们称之为 $ parent $ 树。\(parent\) 树的根就是自动机的起始状态。

   证明其实很简单。\(v\) 的 \(\text{mx}\) 相当于是 \(u\) 的 \(\text{mn}\) 去掉最前面一个字符出来的，所以最多只有一个。而根据定理 3，我们知道必然存在这样一个节点。所以一个 \(u\) 有且仅有一个 \(v\)，也就构成了一棵树。

后缀自动机的构建

考虑一个增量的算法。一个一个加字符并且维护当前的后缀自动机。

首先，我们设上一次构建完自动机之后，最后一个节点为 \(\text{lst}\)，这一次要加入字符 \(a\)。我们肯定要新建一个 \(\text{cur}\) 表示新来的串。\(\text{mx}_{\text{cur}}=\text{mx}_{\text{lst}}+1\)。很容易发现，实际上只会有 \(\text{lst}\) 到根的路径上的这些点的转移边会被修改。下面分情况讨论。

1. \(\text{lst}\) 到根上没有一个节点有向 \(a\) 的转移边。

   直接让每一个点都向 \(a\) 连一个转移边就可以了。\(\text{fa}(\text{cur})\) 就是 \(parent\) 树的根。

2. \(\text{lst}\) 到根上有节点有向 \(a\) 的转移边。

   设从 \(\text{lst}\) 到根，第一个有转移边的点为 \(v\)。那么我们还可以知道 \(v\) 到根的路径上的点都会有向 \(a\) 的转移边（定理 2）。设 \(v\) 向 \(a\) 的转移边指向了 \(p\)。

   下面还要分情况讨论：

   1. \(\text{mx}_{p}=\text{mx}_{v}+1\)

      这说明 \(p\) 能表示的最大的串就是从 \(v\) 转移过来的。不难发现 \(p\) 能表示的串都是 \(\text{cur}\) 能表示的串的后缀。所以此时 \(\text{fa}(\text{cur})=p\)。

   2. \(\text{mx}_{p}\not=\text{mx}_{v}+1\)

      显然 \(\text{mx}_{p}\) 一定 \(>\text{mx}_{v}+1\)。

      此时 \(p\) 所表示的长度 \(\le \text{mx}_{v}+1\) 的那些串的 \(\operatorname{end-pos}\) 增加了 \(\text{cur}\) 这个新位置（定理 2），而 \(> \text{mx}_{v}+1\) 的那些串则没有改变。

      所以将 \(p\) 拆成两个点，一个表示 \(\le \text{mx}_{v}+1\) 的部分 \(p_1\) ，另一个代表 \(>\text{mx}_{v}+1\) 的部分 \(p_2\) 。对于 \(p_1\) ，它就是 \(\text{cur}\) 的 \(\text{fa}\)，\(\text{mx}_{p_1}=\text{mx}_{v}+1\)。对于 \(p_2\)，它的父亲就是 \(p_1\) 。以及，它们两个的转移边是一模一样的。

这样构建的时间是 \(O(n)\) 的（不会证明），点的数量是 \(O(n)\) 的（每次最多增加两个点），边的数量是 \(O(n)\) 的（不会证明）。

后缀自动机的应用

以下会和后缀数组比较。

构建方面，后缀数组的常用算法时间是 $ O(n\log n) $ 的，后缀自动机是稳定的 \(O(n)\) 。不过后缀数组可以用 DC3 或者 SA-IS 来实现 \(O(n)\) 构造。不常用的还有什么用？

处理问题的能力方面：

字符串匹配

事实上，两个都很少用来干这个事情。

好吧我就是不会。

不同子串个数

后缀数组

模板问题，问题复杂度 \(O(n)\)。

后缀自动机

后缀自动机上任意两个点之间的路径都是原串的一个本质不同的字符串，所以可以有这样的 DP：\(f_u\) 表示从 \(u\) 出发可以表示的字符串的数量。

转移：

\[f(u)=1+\sum_{(u,v)\in DAWG} f(v) \]

答案就是 \(f_{r}\)，其中 \(r\) 为自动机的初始状态。

原串中字典序第 K 大的（本质不同的）字符串， [TJOI2015] 弦论

后缀数组

解法未知。

后缀自动机

可以在后缀自动机上面，先计算出每个点出发能表示的串的数量。由于一条边表示一个字符，因此，从一个点出发的边按照字典序存在大小顺序。因此我们可以像平衡树那样在后缀自动机上面构造出第 K 大字符串。

具体请移步题解 [TJOI2015] 弦论。

求两个串的 LCS ，SP1811 LCS - Longest Common Substring

后缀数组

两个串连在一起，然后枚举 $ height $ 求最大值。注意判断下标要分居两个串。时间 $ O(n) $ 。

后缀自动机

先对一个串构建后缀自动机，然后把另一个串放到自动机上面跑。如果失配就跳 $ \text{fa} $。最后记录每次的转移成功（走过了一条合法的转移边，或者不能走到这样的转移边）后的答案。

类比尺取法。跳 \(\text{fa}\) 边就是移动尺取的左端点，走转移边就是移动尺取的右端点。

求多个串的 LCS ，SP1812 LCS2 - Longest Common Substring II

后缀数组

多个串连在一起构建后缀数组。二分答案 $ mid $。把 $ >mid $ 的 $ height $ 分到一组，把 $ \le mid $ 的 $ height $ 分到一组。对于 $ >mid $ 的那一组，检查是否每一个串里面都有一个 $ sa $ 的下标，复杂度 $ O(n\log n) $。

后缀自动机

请移步题解 SP1812 LCS2 - Longest Common Substring II 。

后记

后缀自动机不失为一个处理字符串问题的强大工具。配合其他算法更是如此。

下一次更新未知。

鸣谢：

KesdiaelKen 的史上最通俗的后缀自动机详解，写得很好。

机房巨佬 Tiw_Air_OAO ， PPT 很详细，讲得也很详细。