Backpropagation Through Time (BPTT) 梯度消失与梯度爆炸

Backpropagation Through Time (BPTT) 梯度消失与梯度爆炸

下面的图显示的是RNN的结果以及数据前向流动方向

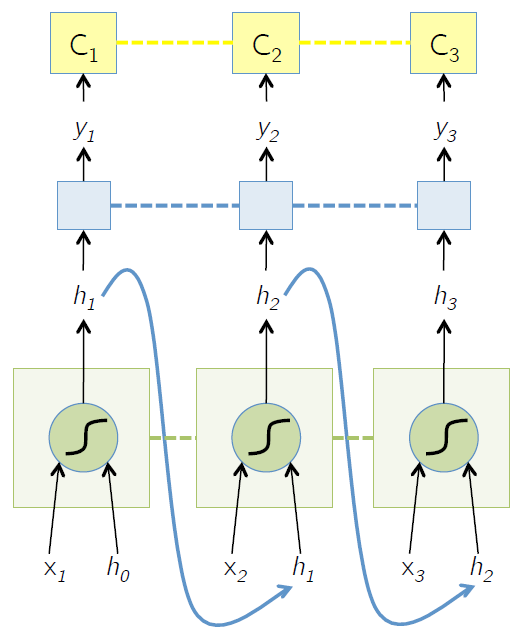
假设有

\[\begin{split} h_t &= \tanh W\begin{pmatrix}x_t \\ h_{t-1}\end{pmatrix}\\ y_t &= F(h_t)\\ C_t &= L(y_t, \hat{y}_t) \end{split} \]

那么在反向传播时，假设我们要求的是

\[\begin{split} \dfrac{\partial C_t}{\partial h_1} &= \dfrac{\partial C_t}{\partial y_t}\dfrac{\partial y_t}{\partial h_1 }\\ &= \dfrac{\partial C_t}{\partial y_t}\dfrac{\partial y_t}{\partial h_t }\dfrac{\partial h_t}{\partial h_{t-1} }\cdots\dfrac{\partial h_2}{\partial h_{1} } \end{split} \]

根据链式法则，其中包含了多个因子的连乘，这就是梯度爆炸和梯度消失的万恶之源。解决这种问题的通用手段就是使用skip connection，让梯度能够穿越一些时间步，直接前传。我们不难发现在LSTM 和GRU中都存在着这样的链接，具体的，在LSTM中，有

\[c_t = f_t\odot c_{t-1} + i_t\odot\hat{c}_{t} \]

在GRU中有

\[h_t = u\odot h_{t-1} + (1 - u)\odot c_t \]