单调栈学习笔记
单调栈基础
单调栈根据所维护的单调性可以分为四种：
- 严格递增栈。必须出栈至栈空或栈顶小于当前元素后，才入栈当前元素。
- 严格递减栈。必须出栈至栈空或栈顶大于当前元素后，才入栈当前元素。
- 非严格递增栈。必须出栈至栈空或栈顶小于等于当前元素后，才入栈当前元素。
- 非严格递减栈。必须出栈至栈空或栈顶大于等于当前元素后，才入栈当前元素。
单调栈基本性质
一些基本性质：
- 维护单调性的方式是：无论破坏多少个栈内的，也要让新元素进来。
- 如果是正着扫序列，则越靠近栈顶的元素，下标越大，距离当前指针越近。
接下来来看单调栈的两个实例。
NGE
NGE 基础
当用到单调栈的时候，95% 都是在解决这个问题。
给定一个数组 \(a\)，对每个 \(i\)，求出 \(i\) 的下一个最近的比 \(a_i\) 大的数的下标 \(f(i)\)，如果不存在则 \(-1\)。
这个问题被称为 Next Greater Element 问题，即 NGE 问题。类似地，我们还有 NLE（Next Less Element），NNGE（Next Not Greater Element），NNLE（Next Not Less Element）问题。这四个问题分别对应四种不同的单调栈，对于 NGE 问题，我们应该选择非严格递减栈：必须出栈至栈空或栈顶大于等于当前元素后，才入栈当前元素。
于是，从左到右扫，每个数都会被入栈一次。如果 \(a_i\) 是 \(a_j\) 进栈时被弹出的，说明 \(a_i < a_j\)，那么 \(f(i) = j\)。如果 \(a_i\) 没被弹出过，\(f(i) = -1\)。至于这具体是为什么，证明省略，网上有很多。
/*
* @Author: crab-in-the-northeast
* @Date: 2022-12-30 02:27:56
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2022-12-30 02:31:37
*/
#include <bits/stdc++.h>
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
typedef std :: pair <int, int> pii;
const int maxn = (int)3e6 + 5;
int ans[maxn];
int main() {
int n = read();
std :: stack <pii> s;
for (int i = 1; i <= n; ++i) {
int x = read();
while (!s.empty() && x > s.top().first) {
ans[s.top().second] = i;
s.pop();
}
s.push({x, i});
}
for (int i = 1; i <= n; ++i)
printf("%d ", ans[i]);
puts("");
return 0;
}
应该选择什么单调栈？
在实际做了一些单调栈题目后，我发现重要的不是你选择哪种单调性的单调栈，而是选择用于求解四个问题（NGE、NLE、NNGE、NNLE）中哪个问题的单调栈。
怎么选呢？假设我们要选择 NGE 单调栈，核心代码是这样的：
for (int i = 1; i <= n; ++i) {
int x = read();
while (!s.empty() && x > s.top().first) {
ans[s.top().second] = i;
s.pop();
}
s.push({x, i});
}
上面的 x > s.top().first 正是我们体现单调栈类型是 NGE 的地方。很好理解，s.top().first 就是栈顶的值，x 就是当前的元素，因为 x > s.top().first，所以栈顶找到了它的 NGE x，直接标记即可。
假设我们要选择 NNGE 单调栈，那么 while 里的条件应该写成：
!s.empty() && x <= s.top().first
因为 x 是栈顶的 Next Not Greater Element（即小于等于栈顶）。
当然，如果你实在想知道单调性和这四个问题的对应关系，这里我也给出：
- NGE 单调栈 = 非严格单调递减栈。
- NNLE 单调栈 = 严格单调递减栈。
- NLE 单调栈 = 非严格单调递增栈。
- NNGE 单调栈 = 严格单调递增栈。
你可以用适合自己的方法记忆。
从 NGE 问题发掘出更多性质
每个时刻单调栈内元素的含义是：待确定 NGE / NLE / NNGE / NNLE 的元素。这个思想尤为重要，可以看做单调栈的第三条性质。
下面我们以 NGE 单调栈为例。
在单调栈刚好射入 \(a_i\) 后，单调栈中的任一元素 \(a_j\)，目前还没有找到它的 NGE。也即，\(a_j\) 的 NGE 要么不存在，要么下标 \(>i\)，现在还没扫到呢。
而先前被插入，后来已不在单调栈内的元素 \(a_{j'}\)，一定有 \(a_{j'}\) 的 NGE 存在，为 \(a_k\)，并且下标 \(j' < k \le i\)。
同时，考虑任意时刻 NGE 单调栈任意两个相邻的元素 \(a_i\) 和 \(a_j\)。设 \(a_i\) 靠近栈底，\(a_j\) 靠近栈顶，明显有 \(i <j\)，\(a_i \ge a_j\)。
如果 \(i < j - 1\)，则 \(a_{j - 1}\) 不在栈里。由于 \(a_{j - 1}\) 上一秒刚进栈，下一秒就被 \(a_j\) 弹出了，所以 \(a_{j - 1} < a_j\)。
如果 \(i < j - 2\)，意味着 \(a_{j - 2}\) 也没在栈里，那它要么被 \(a_{j - 1}\) 弹出去，要么被 \(a_{j}\) 弹出去。所以有 \(a_{j - 2} < a_{j - 1}\) 或 \(a_{j - 2} < a_j\)。无论如何，因为 \(a_{j - 1} < a_j\)，都有 \(a_{j - 2} < a_j\)。
非常类似地，我们可以推出对于任意 \(i < k <j\)，\(a_k < a_j\)。
所以可以推出 \(a_i \ge a_j > a_k\)。
这意味着，非严格单调递减栈中相邻的两个元素，在原序列中间夹着的所有元素，都比这两个元素更小。称之为性质四。
另外，对于 NNLE 栈，上面那个结论是 \(a_i > a_j \ge a_k\)，证明思路类似。
NLE 和 NNGE 就是上面两种情况不等号反过来啦（这里不取等的接着不取等，取等的接着取等哦）。
区间端点最大 / 小问题
题意：统计数对 \((i, j)\) 的数量，满足 \(\max(a[i + 1 \ldots j - 1]) \le \min(a_i, a_j)\)。
让 \(j\) 从 \(1 \to n\)，统计有多少个 \(i\) 满足 \((i, j)\) 满足要求。考虑维护 NGE 栈。
在射入 \(a_j\) 之前，不在单调栈内的元素 \(a_i\)，要么还没进过栈（\(i \ge j\)），要么已经找到了 NGE（即存在一个 \(k\) 满足 \(i < k< j\) 且 \(a_k > a_i\)）。很明显，这两种情况对应的 \((i, j)\) 都是不满足要求的，所以我们只需要在单调栈中找满足条件的 \(a_i\) 即可。
那么满足条件的 \(a_i\) 又有哪些呢？
我们尝试将 \(a_j\) 射入，这样弹出若干次栈顶。设其中任一元素为 \(a_k\)，则 \(a_k\) 的 NGE 为 \(a_j\)。也即，\(a_k\) 下一个比它大的数就是 \(a_j\)，所以 \(\max(a[k + 1\ldots j - 1]) \le a_k < a_j\)，很明显，\((k, j)\) 是满足要求的。
一直弹到不弹为止，很明显，如果此时栈已经为空，那么上面的所有 \((k, j)\) 已经是所有右端点为 \(j\) 的满足条件的数对了（因为不在栈里的一定不是）。
如果栈不为空，设栈顶为 \(a_p\)。则 \(a_p \ge a_j\)。此时如果我们射入 \(a_j\)，那么 \(a_p\) 和 \(a_j\) 就已经相邻了，之前推得的 性质四 说明，\((p, j)\) 也是满足条件的。
那么比 \(a_p\) 还靠近栈底的元素是否满足条件？
分类讨论。
【第一种情况：\(\boldsymbol{a_p = a_j}\)】
考虑栈中等于 \(a_p\) 的其它元素 \(a_q\)。很明显所有满足条件的 \(a_q\) 都聚集在栈的顶部（我们先不急着射 \(a_j\)）。
根据性质四，在原序列中，所有满足条件的 \(a_q\) 之间，\(a_q\) 与 \(a_p\) 之间，\(a_p\) 与 \(a_j\) 之间的元素都 \(< a_p = a_q = a_j\)，所以所有的 \((q, j)\) 也是满足条件的。
考虑比 \(a_q\) 还大，又最靠近栈顶的元素 \(a_r\)。不难发现 \(a_r >a_q\)，而且 \(a_r\) 再往栈顶走一个元素就是 \(a_q\)。考虑 \(a_r\) 和这个 \(a_q\) 之间的元素，同样满足都小于 \(a_q\)。所以 \((r, j)\) 也满足条件。
但是，\(a_r\) 再往栈底走一个元素 \(a_s\)，即使 \(a_r = a_s\)，序列上 \(s\) 到 \(j\) 也会经过 \(a_r > a_j\)，因此 \((s, j)\) 已经不再合法。比 \(a_s\) 更靠近栈底的元素也会经过 \(a_r\)，同理不合法。
【第二种情况：\(\boldsymbol{a_p > a_j}\)】
此时，只有栈顶这个 \(a_p\) 是满足条件的：如果再射入 \(a_j\)，\(a_p\) 和 \(a_j\) 将相邻，中间的元素 \(< a_j < a_p\)，满足条件。
而不在栈顶的其它元素在序列上到 \(a_j\) 一定会经过 \(a_p > a_j\)，不合法，遗憾离场。
到这里本题正确性已经做完了，但事实上上面的 第一种情况，我们还要从栈顶一直往栈底扫，找极长的一个元素相同段，复杂度已经不对了。
怎么办呢？这里有一个小技巧，那就是把栈中相邻的两个相等的元素“打包”，记成一个 pair 元素，其中 pair 的第一项是元素本身，第二项是元素出现了多少次。这样我们只需要获取栈顶信息即可，复杂度正确。
/*
* @Author: crab-in-the-northeast
* @Date: 2023-04-24 19:49:57
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2023-04-24 20:09:39
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
typedef std :: pair <int, int> pii;
signed main() {
int n = read();
std :: stack <pii> s;
int ans = 0;
while (n--) {
int x = read();
while (!s.empty() && x > s.top().first) {
ans += s.top().second;
s.pop();
}
if (s.empty())
s.push({x, 1});
else if (s.top().first == x) {
int cnt = s.top().second;
ans += cnt;
s.pop();
ans += (s.empty() ? 0 : 1);
s.push({x, cnt + 1});
} else {
++ans;
s.push({x, 1});
}
}
printf("%lld\n", ans);
return 0;
}
对于其它类型的端点最值问题，该怎么解决？请接着阅读后面的例题。
例题
USACO06NOV Bad Hair Day S
P2866 USACO06NOV Bad Hair Day S
统计数对 \((i, j)\) 数量，满足 \(a_i > \max(a[i + 1\ldots j])\)。
【思路一】
考虑扫 \(j\) 从 \(1 \to n\) 统计 \((i, j)\) 的数量，并维护 NNLE 栈。
假设现在将要处理 \(a_j\)（刚处理完 \(a_{j - 1}\) 入栈），那么对于任意 \(i <j\)，不在栈中的元素 \(a_i\) 都找到了它的 NNLE，即存在一个 \(k\) 满足 \(i < k < j\) 并且 \(a_i \le a_k\)。这样的 \((i, j)\) 不可能满足要求，因此只需判断单调栈中的元素。
考虑射入 \(a_j\)，这样会弹出若干次栈顶，设弹出的任一元素为 \(a_k\)。此时，\(a_k\) 找到了它的 NNLE \(a_j\)，证明 \(a_k \le a_j\)，很明显 \((k, j)\) 不满足条件。
弹出所有应该弹的元素后，栈内剩下的任一元素 \(a_p\) 仍未找到它的 NNLE，也即，不存在一个 \(k\) 使得 \(p < k \le j\) 满足 \(a_p \le a_k\)。换句话说，所有满足 \(p < k \le j\) 的 \(k\) 都满足 \(a_p > a_k\)，就有 \(a_p > \max(a[p + 1\ldots j])\)。
因此只需要让每个元素入栈时，先把该弹的弹掉，然后累计剩下的栈的大小即可。
/*
* @Author: crab-in-the-northeast
* @Date: 2023-04-25 08:19:16
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2023-04-25 08:21:27
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
signed main() {
int n = read(), ans = 0;
std :: stack <int> s;
while (n--) {
int x = read();
while (!s.empty() && x >= s.top())
s.pop();
ans += s.size();
s.push(x);
}
printf("%lld\n", ans);
return 0;
}
【思路二】
上面这个思路很巧妙，但事实上有一个无脑做法。
考虑满足条件的 \((i, j)\)，对于一个 \(i\)，所有满足条件的 \(j\) 其实就是在 \(a_i\) 和 \(a_i\) 的 NNLE 的两个下标之内的所有下标。
所以直接算 NNLE 即可。
HISTOGRA
SP1805 HISTOGRA - Largest Rectangle in a Histogram
考虑最优矩形，下方一定紧贴地线，上方一定紧贴某个矩形的高。
我们考虑对于给定每条小矩形，计算目标矩形如果在这个矩形上，以这个矩形的高为高，最宽能延伸多少。
然后发现转化成了 PLE（Previous Less Element）和 NLE 问题，用两个 NLE 栈维护，一个正着扫一个倒着扫即可。
/*
* @Author: crab-in-the-northeast
* @Date: 2023-04-25 08:46:59
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2023-04-25 09:02:00
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
inline bool gmx(int &a, int b) {
return b > a ? a = b, true : false;
}
const int maxn = (int)1e5 + 5;
int a[maxn], ple[maxn], nle[maxn];
signed main() {
for (int n = read(); n; n = read()) {
for (int i = 1; i <= n; ++i)
a[i] = read();
std :: stack <int> s;
for (int i = 1; i <= n; ++i) {
while (!s.empty() && a[i] < a[s.top()]) {
nle[s.top()] = i;
s.pop();
}
s.push(i);
}
while (!s.empty()) {
nle[s.top()] = n + 1;
s.pop();
}
for (int i = n; i; --i) {
while (!s.empty() && a[i] < a[s.top()]) {
ple[s.top()] = i;
s.pop();
}
s.push(i);
}
while (!s.empty()) {
ple[s.top()] = 0;
s.pop();
}
int ans = 0;
for (int i = 1; i <= n; ++i)
gmx(ans, a[i] * (nle[i] - 1 - ple[i]));
printf("%lld\n", ans);
}
return 0;
}
POI2008 PLA-POSTERING
首先发现答案和矩形宽度一点关系都没有。忽略！
不难发现一种可行的方案：对每个建筑分别张贴一张海报，这样海报数量为 \(n\)。
我们必须让一张海报同时完全覆盖两个建筑，才能让需要的海报数量变小。
考虑这两个建筑的必要条件：
- 这两个建筑等高。
- 这两个建筑中间没有比这两个建筑低的建筑。
不难发现上面的条件已经充分，我们考虑优先给满足上面条件的两个建筑中间填上矩形。
这样以来矩形可能有重叠，比如按照上面的填涂规则，有如下事例：
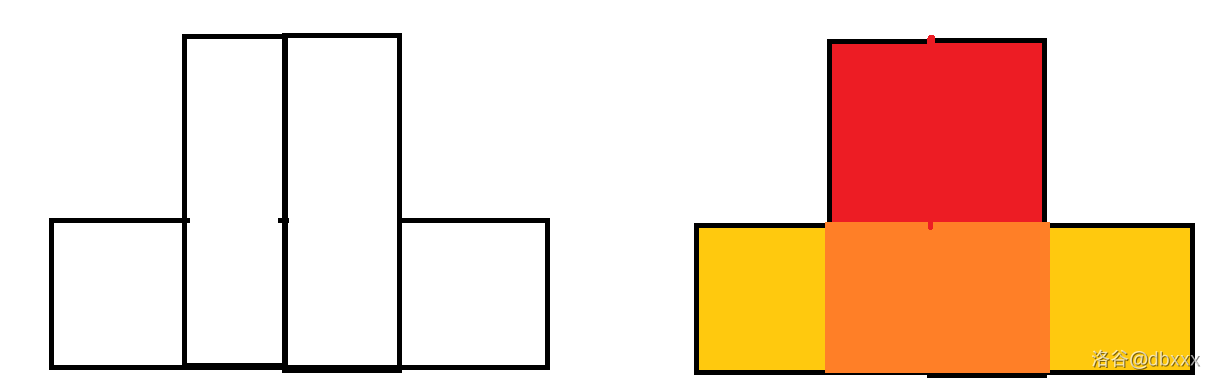
上图中，橙色矩形是红色矩形和黄色矩形的公共部分。
这个问题也很好处理，我们缩减红色的范围，让它的下界只扩展到黄色的上界就可以了。
类似的重叠问题都可以这样解决，优先满足下面的，让上面的只扩展到下面的上界即可。
因此，问题变成统计数对 \((i, j)\) 的数量，满足 \(\max(a[i + 1\ldots j - 1]) > a_i = a_j\)。这是端点最值问题，应用单调栈解决。
统计完这个数量之后，直接用 \(n\) 减去它即可。
解释一下上面为什么是 \(>\) 而不是 \(\ge\)。如果 \((i, j)\) 中间没有比他们高的元素，\((j, k)\) 中间没有比他们高的元素，那么可以有一个矩形精确覆盖 \(a[i \ldots k]\)，这个时候需要的海报数量应该 \(-2\)。而如果是 \(\ge\)，我们会把 \((i, k)\) 也统计上，从而会让需要海报数量 \(-3\)，这不是我们期望的；而改成 \(>\) 就能解决这个问题了。
这个问题怎么做？考虑维护 NNGE 栈，扫 \(j\) 来统计 \((i, j)\) 的数量。
在射入 \(a_j\) 之前，不在栈内的任一元素 \(a_i\) 已经找到了它的 NNGE（Next Not Greater Element），说明存在 \(k\) 使得 \(i < k < j\) 且 \(a_i \ge a_k\)，这样以来 \((i, j)\) 已经不合法。
只用考虑栈内的元素。
考虑弹出为了射入 \(a_j\) 应该弹出的元素 \(a_k\)，有 \(a_k\) 的 NNGE 是 \(a_j\)，也即 \(a_{k + 1}\) 到 \(a_{j - 1}\) 这一段严格比 \(a_k\) 大。这个时候，如果 \(a_k > a_j\)，则 \((k, j)\) 不合法；如果 \(a_k = a_j\)，则 \((k, j)\) 合法。
再考虑栈内剩余的任一元素 \(a_p\)，有 \(a_p < a_j\)，不合法。
所以只需要维护严格递增栈的同时，弹出栈顶的时候看栈顶有没有和元素相同的即可。
/*
* @Author: crab-in-the-northeast
* @Date: 2023-04-25 13:36:30
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2023-04-25 13:52:14
*/
#include <bits/stdc++.h>
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
int main() {
int n = read(), ans = n;
std :: stack <int> s;
for (int i = 1; i <= n; ++i) {
read(); int x = read();
while (!s.empty() && x <= s.top()) {
if (s.top() == x)
--ans;
s.pop();
}
s.push(x);
}
printf("%d\n", ans);
return 0;
}
我们已经看了两道类似端点最值问题的习题了，大概总结一下方法⑧。
首先，我们要明确，这种问题找到合法 \((i, j)\) 的过程一般都是扫 \(j\) 维护单调栈，看满足条件的 \(i\) 有多少个。而且，不在单调栈里的 \(a_i\) 对应的 \(i\) 一定不合法。
那么怎么确定找那种类型的单调栈呢？看已经确定了 \(\boldsymbol{a_i}\) 的 NGE，NNGE，NLE，NNLE 的四项中的哪一项时，\(\boldsymbol{(i, j)}\) 一定不合法。举个例子吧：
统计数对 \((i, j)\) 的数量，满足 \(\max(a[i + 1 \ldots j - 1]) \le \min(a_i, a_j)\)。
为方便判断，我们将上面的最值形式做一些转化。首先就是先把 关于 \(\boldsymbol{a_j}\) 的限制砍去，即
满足 \(\max(a[i + 1 \ldots j - 1]) \le a_i\)。
然后 将最值转成“对于任意 \(\boldsymbol k\)”这种形式，也即
满足对于任意 \(i < k < j\) 都有 \(a_k \le a_i\)。
考虑 什么时候会破坏这个条件，显然，就是
满足存在 \(i < k < j\) 使得 \(a_k > a_i\)。
也就是 \(a_i\) 找到了它的 NGE，判断成功，我们应该维护 NGE 栈，这样以来，不在栈内的元素就意味着找到 NGE，找到 NGE 就意味着不合法。
再来看这个例子：
统计满足 \(\max(a[i + 1\ldots j - 1]) < a_i = a_j\)。
首先砍去 \(a_j\) 限制：
满足 \(\max(a[i + 1\ldots j-1]) < a_i\)。
最值转任意 \(k\)：
对于任意 \(i < k < j\) 有 \(a_k < a_i\)。
破坏：
存在一个 \(i < k < j\) 有 \(a_k \ge a_i\)。
所以用 NNLE 栈。
另外，上面那个 Bad Hair Day S 的思路一，也可以看成端点最值问题（只是不再将 \(a_j\) 看成端点了），所以用上面的方法也能很方便判断出应该使用什么栈，可以自己试试。
判断完应该使用哪个栈之后，剩余的部分就是看栈里的什么元素满足条件，一般分为两种看：
- 为射入 \(a_j\)，要弹出的元素。
- 射入 \(a_j\) 后仍为弹出的元素。
根据一些取等细节，上面两类可能分为更细的类，需要自己判断。
长方形
对于每个 \(i\) 从 \(1 \to n\)，统计底边在第 \(i\) 行下边界的矩形数量。
从每个点 \((i, j)\) 出发向上往上最多能延伸多少，这个是可以 \(\Theta(nm)\) 预处理的。
然后就变成了 \(n\) 次计数版的 HISTOGRA。问题转化成：
HISTOGRA，但是计算矩形的数量。
考虑一下怎么做。
对第 \(i\) 个矩形，仍然设高度 \(h_i\)，其 PLE 的下标为 \(l_i\)，NLE 的下标为 \(r_i\)。那么从这个点开始，延伸的区域最多是 \([l_i +1, r_i - 1]\)，尝试直接统计 \(h_i \times (i - l_i) \times (r_i - i)\)。
这样以来可能会有重复计数吗？
考虑并排放置的两个等高小矩形，即 \(h_i = h_{i +1}\)，则横长落在 \([i, i +1]\) 这个区间内的所有小矩形都会被 \(h_i \times (i - l_i) \times (r_i - i)\) 和 \(h_{i +1} \times (i + 1 - l_{i + 1}) \times (r_{i + 1} - i - 1)\) 分别统计一次，有重复计数。
怎么办呢？考虑更换 \(r_i\) 的定义：\(h_i\) 的 NNGE 为 \(r_i\)。分析发现，原来的 \(r_i > i +1\)，现在的 \(r_i = i + 1\)，所以 \(h_i \times (i - l_i) \times (r_i - i)\) 不再会对 \(i + 1\) 那一列里的矩形计数，解决了重复计数问题。
我们验证一下是否真的不重不漏了。
每次以 \(i\) 为中心扩展时，统计了所有以 \([l_i + 1, i]\) 内某个点为左端点，以 \([i, r_i - 1]\) 内某个点为右端点的所有矩形。我们尝试证明：对于任意 \(L \le R\)，有且仅有一个 \(i\)，满足 \(L \in [l_i + 1, i]\) 且 \(R \in [i, r_i - 1]\)。
首先很明显，满足条件的 \(i \in [L, R]\)。
其次，考虑找到 \(h[L \ldots R]\) 中取得最小值的 \(h_i\)，如果有多个最小值，取 \(i\) 最大的一个。于是有：对于任意 \(L \le j < i\)，有 \(h_j \ge h_i\)，对于任意 \(i < k \le R\)，有 \(h_k > h_i\)（这里不取等号是因为 \(i\) 在所有最小值中下标最大）。
很明显，\(h_i\) 的 PLE 下标 \(<L\)，即 \(l_i < L\)，\(h_i\) 的 NNGE \(>R\)，即 \(r_i > R\)。这个 \(i\) 满足条件。
对于任意 \(L \le j < i\)，有 \(h_j \ge h_i\)，这说明 \(h_j\) 的 NNGE 下标至少不会超过 \(i\)，即 \(r_j \le i\)。因为 \(i \le R\)，所以 \(r_j \le R\)，\(R\) 不落在 \([j, r_j - 1]\) 内部，\(j\) 不合法。
对于任意 \(i < k \le R\)，有 \(h_i <h_k\)，这说明 \(h_k\) 的 LPE 下标至少不会小于 \(i\)，即 \(l_k \ge i\)。因为 \(i \ge L\)，所以 \(l_k \ge L\)，\(L\) 不落在 \([l_k + 1, k]\) 内部，\(k\) 不合法。证毕。
也就是说，对于任何一个左端点为 \(L\)，右端点为 \(R\) 的矩形，只会在扫到 \(h\) 在 \([L, R]\) 内最靠右的最小值这个点的时候才会被统计到。验证成功。
/*
* @Author: crab-in-the-northeast
* @Date: 2023-04-25 17:53:24
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2023-04-25 18:04:25
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
inline char rech() {
char ch = getchar();
while (!isgraph(ch))
ch = getchar();
return ch;
}
const int maxm = 1005;
int h[maxm], ple[maxm], nnge[maxm];
signed main() {
int ans = 0, n = read(), m = read();
while (n--) {
for (int i = 1; i <= m; ++i)
h[i] = (rech() == '.') ? (h[i] + 1) : 0;
std :: stack <int> s;
for (int i = 1; i <= m; ++i) {
while (!s.empty() && h[i] <= h[s.top()]) {
nnge[s.top()] = i;
s.pop();
}
s.push(i);
}
while (!s.empty()) {
nnge[s.top()] = m + 1;
s.pop();
}
for (int i = m; i; --i) {
while (!s.empty() && h[i] < h[s.top()]) {
ple[s.top()] = i;
s.pop();
}
s.push(i);
}
while (!s.empty()) {
ple[s.top()] = 0;
s.pop();
}
for (int i = 1; i <= m; ++i)
ans += h[i] * (i - ple[i]) * (nnge[i] - i);
}
printf("%lld\n", ans);
return 0;
}
