[luogu p8338] [AHOI2022] 排列
P8338 [AHOI2022] 排列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
对于一个长度为
该排列的第
容易证明任意排列的任意次幂都是一个排列。
定义排列
给出一个长度为
求
-
-
首先明确一下排列的基本定义:长度为
观察题目中排列的幂的定义,从
考虑对于长度为
发现这个图会是一堆简单环构成的(可以有自环),这是因为图
这么建图我们的目的在于将
举个例子:
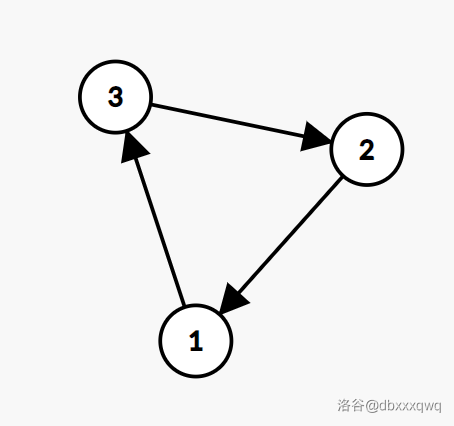
第
现在所有小人顺着走一步。第
另外很显然
然后所有小人再顺着走一步,第
然后再走一步,得到
那么接下来肯定又会有
事实上所有排列的幂都一定会出现循环,而循环节的长度正是
定义排列
我们知道,
那么
设总共有
举个例子,我们对
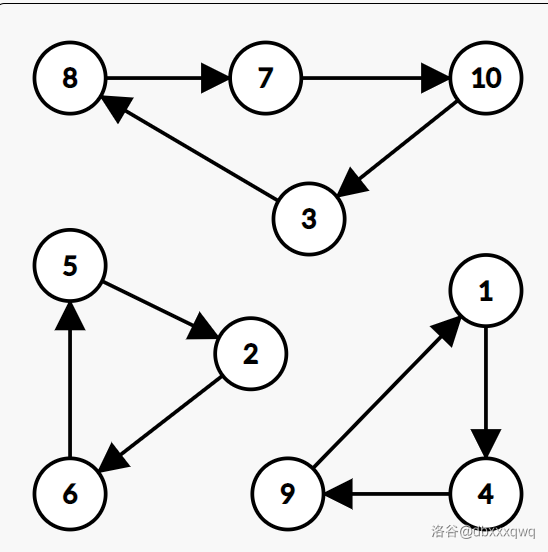
发现总共有
现在来把视线转移到排列
对于整数
,定义 :若存在 使得 ,则 ,否则设排列 为将排列 的第 项 和第 项 交换后得到的排列,则 。
分别考虑。
什么时候存在
先来看
考虑在
也就是说:
否则,怎么求
考虑交换
由于我们现在知道,
交换
发现这样修改,相当于将
证明:假设
举个例子,假设

现在考虑从
然后就会变成这样:
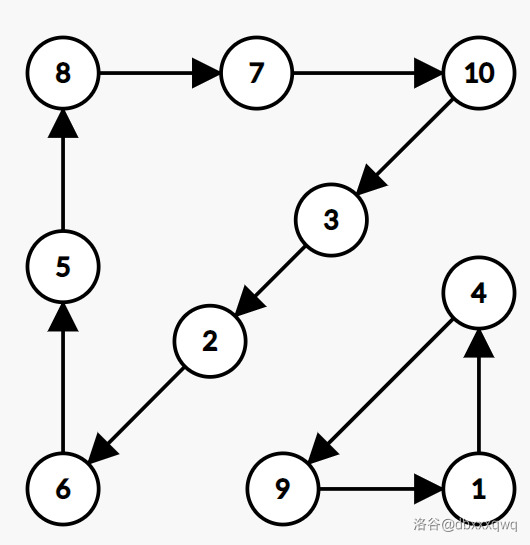
可以看到确实是
所以
上面这个例子中就是
到这里已经理论可做了,我们已经大体完成了翻译题目的工作。现在考虑加速最后结果的计算。
还是上面那个图,再放一次:

我们把目标锁定在上面那个环和左下角那个环。会发现,从上面那个环随便选一个点,从左下角那个环随便选一个点,交换,结果肯定是
再把目标锁定在上面那个环和右下角那个环,发现随便选之后答案仍然是
那有不是
为什么会这样呢?发现他跟我们选取两个点所在的环的长度有关系。选取两个点所在环长度分别是
如果两个环的长度相同,我们可以认为他们的本质是相同的,设本质不同的环总共有
我们知道,环长总和不能超过
这是一个经典结论:如果
,那么值不同的 的种类是 量级的(而且不满)。
因此只要枚举本质不同的环长,进行计算。
我们设
需要分两种情况讨论:
根据对称性,上面的第一种情况中,也可以直接把
由于枚举的开销是
到这里复杂度是
我们发现原题实际上就是想维护一个可重集合的
但是发现
于是有了这样的启发:考虑对每个
注意这里有一个小技巧:将
那么就可以转化为维护若干个质数幂(所有环长的质因数分解出来的所有质因子幂的并集,同样,是可重集),支持询问删除
然后发现一开始那个集合只用记录下所有质因子幂中,每个质数对应最大的
所以询问直接暴力删暴力加暴力获取最大值即可,一次询问中,每个质因数的暴力都是小常数级别的,所以单次询问是
总复杂度
另外,实际上不需要建图,只需要写一个维护大小的并查集即可。
单组数据
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool flag = true;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-')
flag = false;
ch = getchar();
}
while (isdigit(ch)) {
x = (x << 1) + (x << 3) + ch - '0';
ch = getchar();
}
if(flag)
return x;
return ~(x - 1);
}
inline bool updmax(int &x, int y) {
return y > x ? x = y, true : false;
}
const int maxn = 500005;
const int maxm = 805; // sqrt(maxn)
const int mod = (int)1e9 + 7;
int a[maxn];
int inv[maxn], pfmin[maxn]; // prime factor min,存放了一个数的最小质因子。
int pr[maxn], pcnt = 0;
bool isp[maxn];
int lcm = 1;
std :: vector <std :: pair <int, int> > pfs[maxn];
// pfs[i] 存的是 i 的质因数分解,为一个 pair <int, int> 数组。
// pair 的第一个元素是质因子,第二个元素是质因子对应的幂(不是指数,因为在这个题里没必要)。
// 具体看代码,代码比这些文字好懂。
inline void pre(int n = maxn - 5) {
inv[1] = pfmin[1] = 1;
for (int i = 2; i <= n; ++i)
inv[i] = (mod - mod / i) * inv[mod % i] % mod;
std :: memset(isp, true, sizeof(isp));
for (int i = 2; i <= n; ++i) {
if (isp[i]) {
pr[++pcnt] = i;
pfmin[i] = i;
}
for (int j = 1; j <= pcnt && i * pr[j] <= n; ++j) {
isp[i * pr[j]] = false;
pfmin[i * pr[j]] = pr[j];
if (i % pr[j] == 0)
break;
}
}
for (int i = 2; i <= n; ++i) {
int t = i;
while (t != 1) {
int p = pfmin[t], q = 1;
while (t % p == 0) {
q *= p;
t /= p;
}
pfs[i].emplace_back(p, q);
// printf("%lld %lld %lld\n", i, p, q);
}
}
}
int siz[maxn], fa[maxn];
inline int find(int x) {
while (x != fa[x])
x = fa[x] = fa[fa[x]];
return x;
}
inline void uni(int x, int y) {
x = find(x);
y = find(y);
if (x == y)
return ;
if (siz[x] > siz[y])
x ^= y ^= x ^= y;
fa[x] = y;
siz[y] += siz[x];
}
int cnt[maxn];
std :: vector <int> f[maxn];
inline void insert(int x) {
// printf("%lld\n", x);
for (auto v : pfs[x]) {
int p = v.first, q = v.second;
// printf("%lld %lld\n", p, q);
f[p].push_back(q);
std :: sort(f[p].begin(), f[p].end(), std :: greater <int> ());
// 这里 sort 可以看做常数级别,因为 f[p] 始终大小不超过 3
if (f[p].size() > 3)
f[p].pop_back();
}
return ;
}
int s[maxm], m;
std :: vector <std :: pair <int, int> > g[maxn];
// g[p][i] 表示第 i 个关于质数 p 的幂的修改,first 表示幂的值,second 表示修改量。
// 这个是我们的修改实现,举例说明:
// 删除 12 这个数,先质因数分解 2 ^ 2 * 3
// 然后转化成删掉两个质因子幂,一个 2 ^ 2,一个 3。
// 相当于我们把 2 ^ 2 和 3 的出现次数在集合中分别削了 1,所以 -1 就是两个修改的修改量
// 具体看代码。
int tcnt[maxn];
inline int getv(int p) {
int z = 1;
for (int q : f[p])
++tcnt[q];
for (auto v : g[p])
tcnt[v.first] += v.second;
for (int q : f[p]) {
if (tcnt[q] != 0) {
// 注意!!为什么这里要写成 != 0 而不能是 > 0!!!
// 首先,我们想:tcnt[q] 有可能小于 0 吗?
// 其实是可以构造的,只需要让 f[p][2] 这个质因子幂被删两次就可以了。
// (也就是说 f[p][2] 和 f[p][3](事实上没有)这两个质因子幂相同,而且恰好都被删,
// 但是因为 f[p][3] 因为只存前三个的原则并没有记录,所以 f[p][2] 会被记录一次删除两次。
// 所以 tcnt[q] < 0 是有可能的。
// 由于我们 tcnt[q] 是边扫边清零的(看下面第二行),为了清零成功,我们需要把 < 0 的也清零。
// updmax(z, q) 会被影响吗?
// 我们一次最多删两个数,那么 f[p][2] 被删了两次,f[p][0] 和 f[p][1] 肯定没被删过。
// 那么这一轮的 z 肯定会成功识别出 f[p][0],所以没有影响。
updmax(z, q);
tcnt[q] = 0;
}
}
for (auto v : g[p]) {
int q = v.first;
if (tcnt[q] != 0) {
// 这里同上,不能写 > 0。
// 这里 < 0 是因为可能会有删掉的质因子幂因为不是前三大没记录在 f 中。
updmax(z, q);
tcnt[q] = 0;
}
}
return z;
}
inline void modify(int x, int val) {
for (auto v : pfs[x]) {
int p = v.first, q = v.second;
(lcm *= inv[getv(p)]) %= mod;
g[p].push_back(std :: make_pair(q, val));
(lcm *= getv(p)) %= mod;
// 把 lcm 暴力除以原来 p 这里的贡献,修改之后再暴力乘回去。
}
}
inline void rec(int x) {
for (auto v : pfs[x])
g[v.first].clear();
// 清空修改
}
inline void init(int n = maxn - 5) {
std :: fill(siz + 1, siz + 1 + n, 1);
std :: iota(fa + 1, fa + 1 + n, 1);
std :: memset(cnt, 0, sizeof(cnt));
std :: memset(s, 0, sizeof(s));
m = 0;
for (int i = 1; i <= n; ++i)
f[i].clear();
lcm = 1;
}
signed main() {
int T = read();
pre();
while (T--) {
init();
int n = read();
for (int i = 1; i <= n; ++i) {
a[i] = read();
uni(i, a[i]);
}
for (int i = 1; i <= n; ++i) {
if (find(i) == i) {
++cnt[siz[i]];
insert(siz[i]);
// printf("%lld ", siz[i]);
}
}
for (int i = 1; i <= n; ++i)
if (cnt[i] > 0)
s[++m] = i;
for (int i = 1; i <= n; ++i) {
if (!f[i].empty())
(lcm *= f[i][0]) %= mod;
// 初始 lcm
}
// printf("%lld\n", lcm);
int ans = 0;
for (int i = 1; i <= m; ++i) {
int u = s[i];
if (cnt[u] >= 2) {
// puts("meitain");
int org = lcm;
modify(u << 1, 1);
modify(u, -2);
// printf("%lld\n", lcm);
(ans += lcm * cnt[u] % mod * u % mod * (cnt[u] - 1) % mod * u % mod) %= mod;
rec(u << 1);
lcm = org;
}
for (int j = i + 1; j <= m; ++j) {
int v = s[j], org = lcm;
modify(u + v, 1);
modify(u, -1);
modify(v, -1);
(ans += 2 * lcm % mod * cnt[u] % mod * u % mod * cnt[v] % mod * v % mod) %= mod;
rec(u + v);
rec(u);
rec(v);
lcm = org;
}
}
printf("%lld\n", ans);
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】